การแก้ระบบสมการเชิงเส้นสองตัวแปร โดยใช้กราฟ
บทความนี้ได้รวบรวมความรู้เรื่อง การแก้ระบบสมการเชิงเส้นสองตัวแปร โดยใช้กราฟ ทำได้โดยนำตัวเลขแทนค่าตัวแปร แล้วจะได้กราฟของสมการเชิงเส้นสองตัวแปรเป็นกราฟเส้นตรง สังเกตกราฟที่ได้ว่าตัดกัน ขนานกัน หรือทับกัน ลักษณะกราฟจะบอกคำตอบของระบบสมการ ซึ่งก่อนที่จะเรียนเรื่องนี้ น้องๆสามารถศึกษาเรื่อง กราฟของสมการเชิงเส้นสองตัวแปร สามารถศึกษาเพิ่มเติมได้ที่ ⇒⇒ กราฟของสมการเชิงเส้นสองตัวแปร ⇐⇐
สมการเชิงเส้นสองตัวแปร คือ สมการที่มีตัวแปรสองตัว เลขชี้กำลังของตัวแปรแต่ละตัวเป็น 1 และไม่มีการคูณกันของตัวแปร เช่น 2x + 3y – 15 = 0, x + y – 1 = 0, x – 2y = 3 เป็นต้น
รูปมาตรฐานของสมการเชิงเส้นสองตัวแปร
เรียก y = ax + b ว่า รูปมาตรฐานของสมการเชิงเส้นสองตัวแปร ซึ่งอาจเขียนในรูป y = mx + b โดยที่ a หรือ m คือ ความชันของเส้นตรง
1. เมื่อ m > 0 กราฟจะมีลักษณะเป็นเส้นตรงที่ทำมุมแหลมกับแกน X
โดยวัดจากแกน X ในทิศทางทวนเข็มนาฬิกา
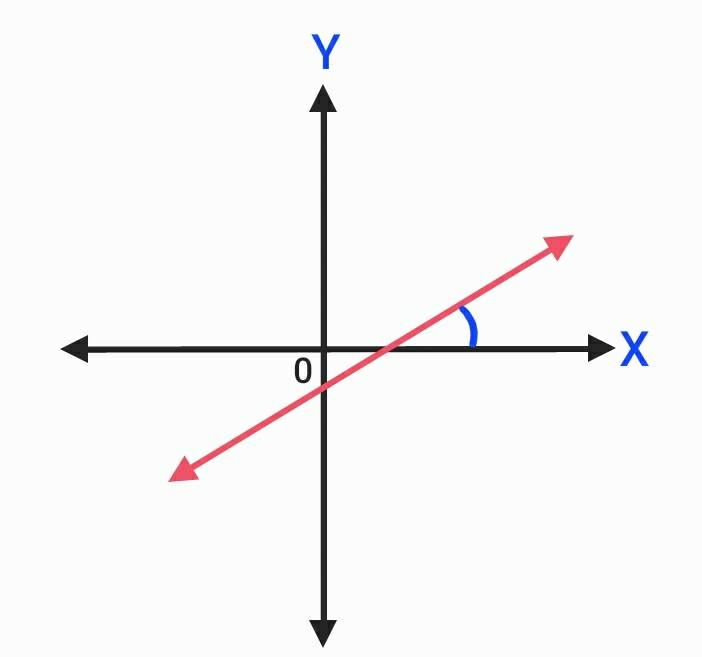
2. เมื่อ m < O กราฟจะมีลักษณะเป็นเส้นตรงที่ทำมุมป้านกับแกน X
โดยวัดจากแกน X ในทิศทางทวนเข็มนาฬิกา
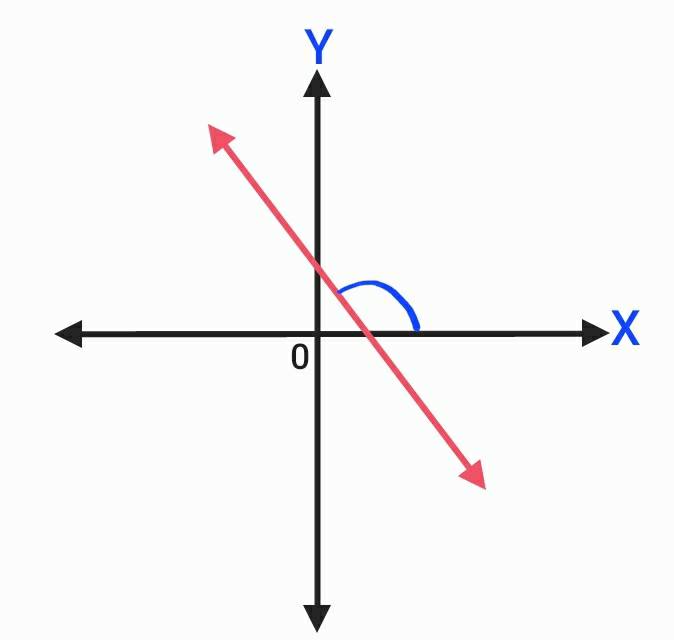
3. เมื่อ m = 0 กราฟจะมีลักษณะเป็นเส้นตรงที่ขนานกับแกน X
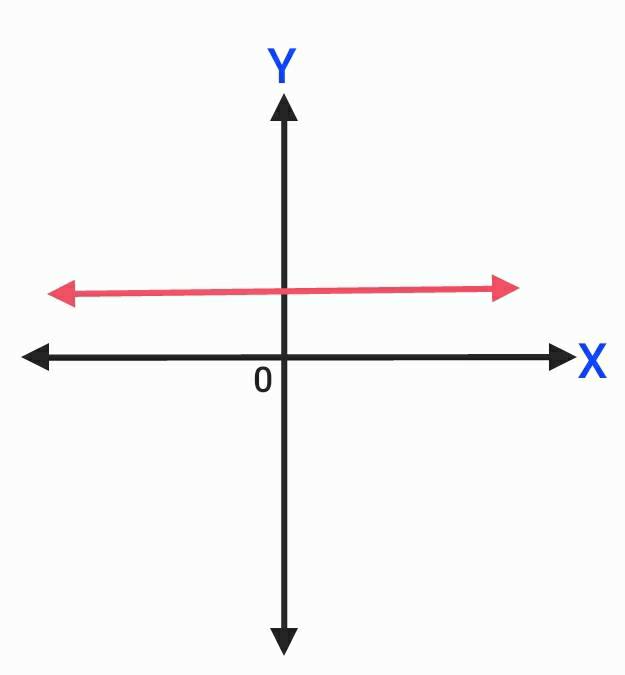
รูปทั่วไปของสมการเชิงเส้นสองตัวแปร คือ Ax + By + C = 0 เมื่อ x, y เป็นตัวแปร และ A, B, C เป็นค่าคงตัว โดยที่ A และ B ไม่เท่ากับศูนย์พร้อมกัน กราฟของสมการนี้จะเป็นเส้นตรง เรียกว่า กราฟเส้นตรง
กราฟของระบบสมการเชิงเส้นสองตัวแปร
กราฟของระบบสมการจะมีลักษณะ ดังนี้
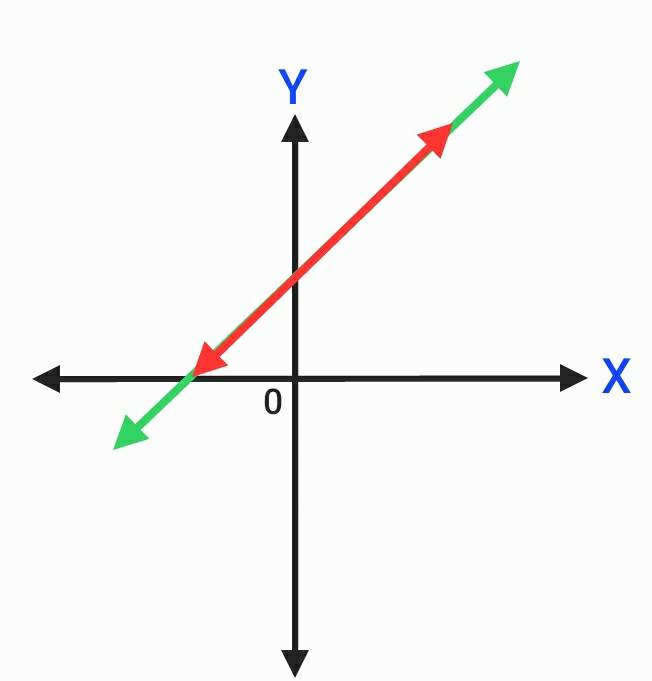
- กราฟของสมการทั้งสองตัดกันที่จุดจุดหนึ่ง ซึ่งจุดนั้นจะเป็นคำตอบของระบบสมการ โดยแสดงค่าของ x และ y ดังรูป
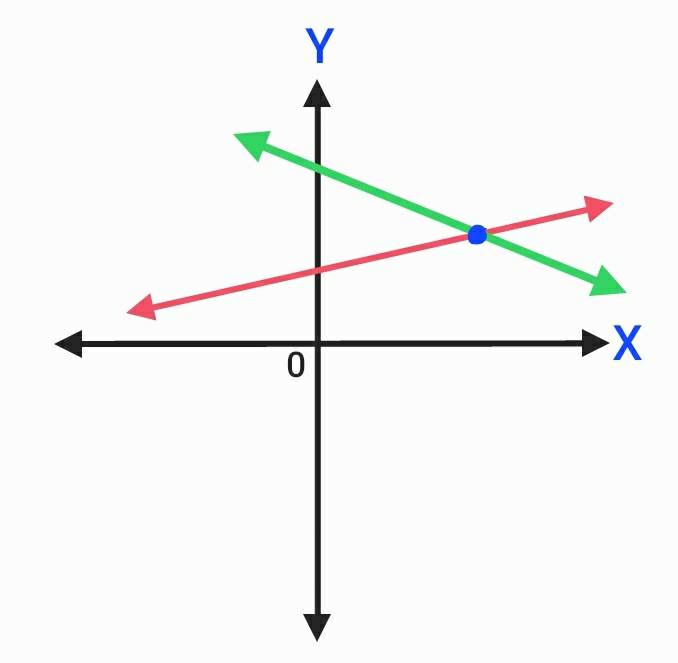
2. กราฟของสมการทั้งสองขนานกัน ซึ่งไม่มีคำตอบของระบบสมการ
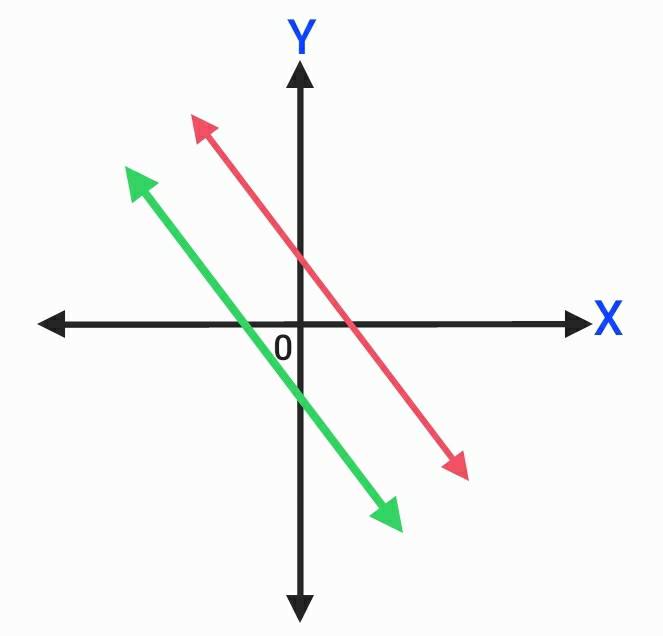
- กราฟของสมการทั้งสองทับกันเป็นเส้นตรงเดียวกัน ซึ่งคำตอบของระบบสมการมีมากมายหลายคำตอบ โดยค่าของ x และ y ที่อยู่บนเส้นตรงนั้น
การใช้กราฟหาคำตอบของระบบสมการเชิงเส้นสองตัวแปร
ตัวอย่างที่ 1 จงหาคำตอบของระบบสมการต่อไปนี้โดยใช้กราฟ พร้อมทั้งระบุว่าระบบสมการนั้น มี 1 คำตอบ มีหลายคำตอบ หรือไม่มีคำตอบ
1) 2x + y = 11
y – x = 8
วิธีทำ 2x + y = 11 ⇒ y = 11 – 2x
y – x = 8 ⇒ y = 8 + x
จาก y = 11 – 2x
แทน x = 2 จะได้ y = 11 – 2(2) = 11 – 4 = 7 ⇒ (2,7)
แทน x = 0 จะได้ y = 11 – 2(0) = 11 – 0 = 11 ⇒ (0,11)
แทน x = -2 จะได้ y = 11 – 2(-2) = 11 + 4 = 15 ⇒ (-2,15)
จาก y = 8 + x
แทน x = 2 จะได้ y = 8 + 2 = 10 ⇒ (2,10)
แทน x = 0 จะได้ y = 8 + 0 = 8 ⇒ (0,8)
แทน x = -2 จะได้ y = 8 – 2 = 6 ⇒ (-2,6)
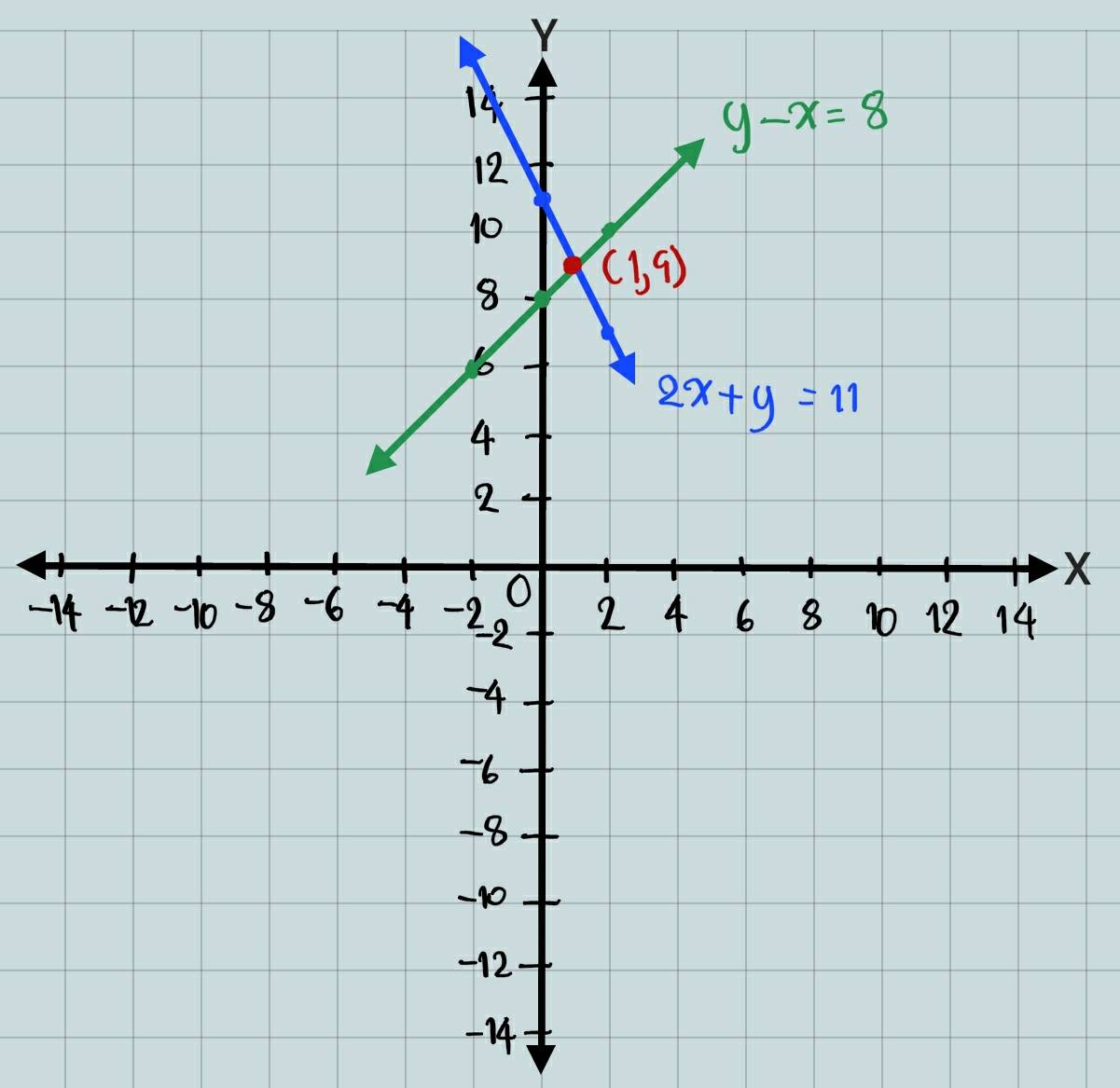
จะเห็นว่า กราฟของระบบสมการตัดกันที่จุด (1,9)
ดังนั้น คำตอบของระบบสมการมี 1 คำตอบ คือ (1,9)
2) 2y − 4x = 6
x − 2y = 4
วิธีทำ 2y − 4x = 6 ⇒ y = (6 + 4x) ÷ 2 = 3 + 2x
x − 2y = 4 ⇒ y = 4 + 2x
จาก y = 3 + 2x
แทน x = 1 จะได้ y = 3 + 2(1) = 3 + 2 = 5 ⇒ (1,5)
แทน x = 0 จะได้ y = 3 + 2(0) = 3 + 0 = 3 ⇒ (0,3)
แทน x = -1 จะได้ y = 3 + 2(-1) = 3 – 2 = 1 ⇒ (-1,1)
จาก y = 4 + 2x
แทน x = 1 จะได้ y = 4 + 2(1) = 4 + 2 = 6 ⇒ (1,6)
แทน x = 0 จะได้ y = 4 + 2(0) = 4 + 0 = 4 ⇒ (0,4)
แทน x = -1 จะได้ y = 4 + 2(-1) = 4 – 2 = 2 ⇒ (-1,2)
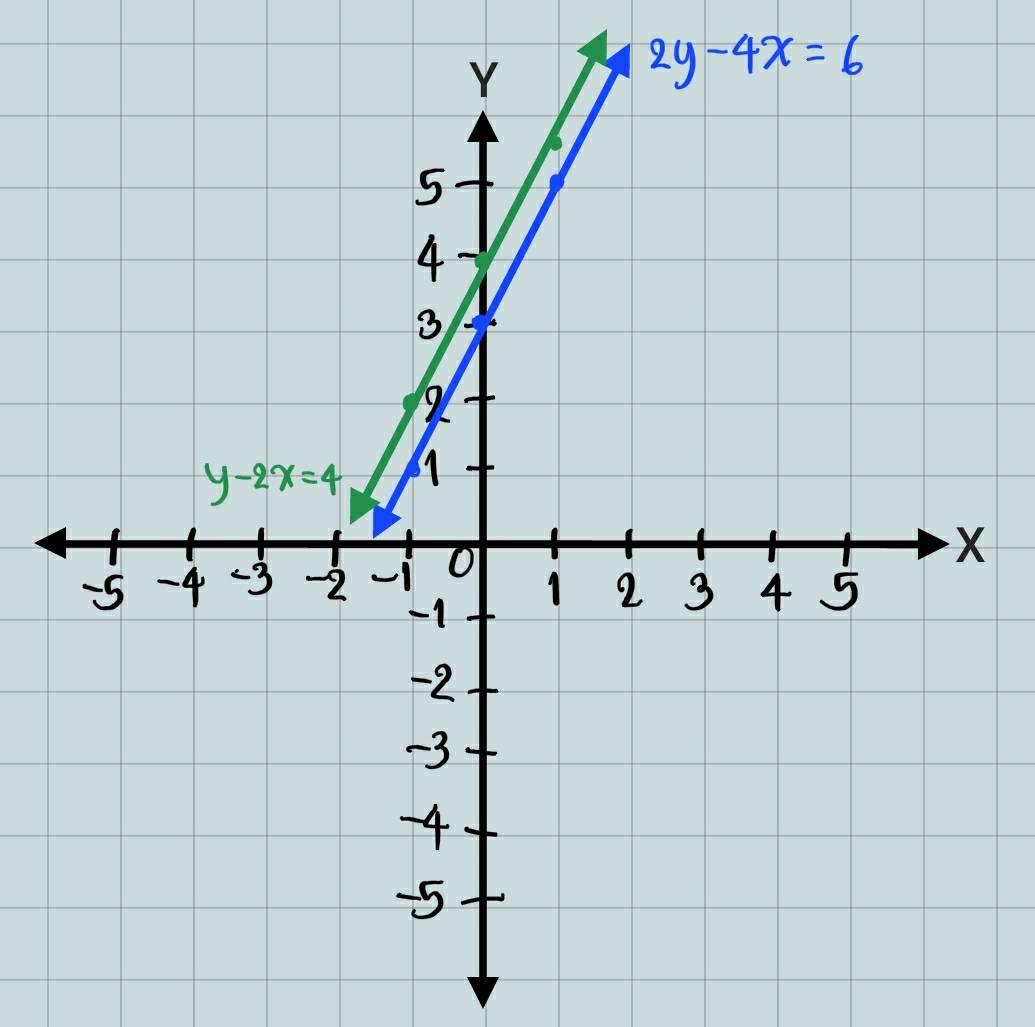
จะเห็นว่า กราฟทั้งสองขนานกัน จึงไม่มีโอกาสตัดกัน
ดังนั้น ระบบสมการไม่มีคำตอบ
3) x – y = 5
y – x = -5
วิธีทำ x – y = 5 ⇒ y = x – 5
y – x = -5 ⇒ y = -5 + x
จาก y = x – 5
แทน x = 1 จะได้ y = 1 – 5 = -4 ⇒ (1,-4)
แทน x = 0 จะได้ y = 0 – 5 = -5 ⇒ (0,-5)
แทน x = -1 จะได้ y = -1 – 5 = -6 ⇒ (-1,-6)
จาก y = -5 + x
แทน x = 1 จะได้ y = -5 + 1 = -4 ⇒ (1,-4)
แทน x = 0 จะได้ y = -5 + 0 = -5 ⇒ (0,-5)
แทน x = -1 จะได้ y = -5 – 1 = -6 ⇒ (-1,-6)
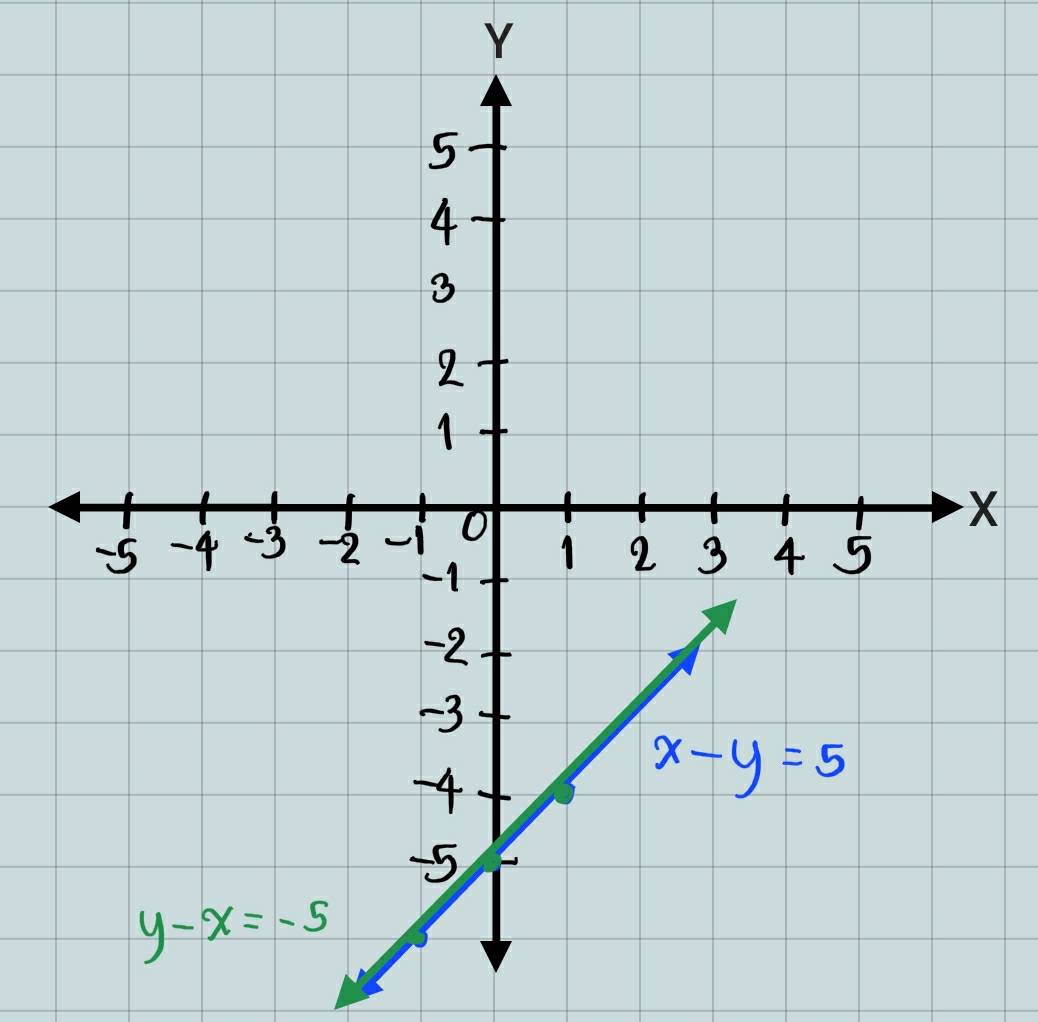
จะเห็นว่า กราฟทั้งสองทับกันสนิท
ดังนั้น ระบบสมการมีหลายคำตอบ
การแก้ระบบสมการเชิงเส้นสองตัวแปร โดยใช้กราฟ ารแก้ระบบสมการเชิงเส้นสองตัวแปรโดยใช้ อาจไม่สะดวกมากนัก เนื่องจากเสียเวลามาก และในบางครั้งคำตอบที่ได้จากกราฟ อาจพิจารณาหาคำตอบได้ยากอาจมีความคลาดเคลื่อนได้บ้าง จึงต้องอาศัยวิธีการอื่นในการแก้ระบบสมการเชิงเส้นสองตัวแปร ซึ่งจะได้เรียนในลำดับถัดไป



















