ค่าของฟังก์ชันไซน์และโคไซน์

supanaree

คณิตศาสตร์, คณิตศาสตร์เพิ่มเติม, ฟังก์ชันตรีโกณมิติ, ม.5

Add LINE friends for one click to find article.

ค่าของฟังก์ชันไซน์และโคไซน์

ค่าของฟังก์ชันไซน์และโคไซน์ จะเกี่ยวข้องกับ θ พิกัดของ จุด (x, y) ซึ่งในบทความนี้จะอธิบายเกี่ยวกับ ความสัมพันธ์ระหว่าง x, y กับ θ

จากบทความที่ผ่านมาเราได้รู้จักวงกลมหนึ่งหน่วยและการวัดความยาวส่วนโค้ง ในบทความนี้น้องๆจะได้รู้จักกับฟังก์ชันไซน์ (sine function) และฟังก์ชันโคไซน์ (cosine function) และวิธีการหาค่าของฟังก์ชันทั้งสอง

Sine function = {(θ, y) | y = sinθ}

cosine function = {(θ, x) | x = cosθ}

จาก P(θ) = (x, y) และจาก x = cosθ และ y = sinθ

จะได้ว่า P(θ) = (cosθ, sinθ)

โดเมนและเรนจ์ของ sine function และ cosine function

โดเมนของฟังก์ชันไซน์และโคไซน์ คือ จำนวนจริง นั่นคือ θ ∈ $\mathbb{R}$

เรนจ์ของฟังก์ชันไซน์และโคไซน์คือ [-1, 1] นั่นคือ ค่าของ cosθ และ sinθ จะอยู่ในช่วง [-1, 1]

ความสัมพันธ์ของฟังก์ชันไซน์และโคไซน์

พิจารณาสมการวงกลมหนึ่งหน่วย (รัศมีเป็น 1) x² + y² = 1

เมื่อแทน x = cosθ และ y = sinθ ในสมการของวงกลมหนึ่งหน่วย

จะได้ว่า (cosθ)² + (sinθ)² = 1 สามารถเขียนได้อีกรูปแบบหนึ่ง คือ

cos²θ + sin²θ = 1

การหา ค่าของฟังก์ชันไซน์และโคไซน์

การหาค่าฟังก์ชันไซน์และโคไซน์นั้น น้องๆจะต้องมีพื้นฐานเรื่องความยาวส่วนโค้งและพิกัดจุดปลายส่วนโค้งพร้อมทั้งรู้เรื่องจตุภาคด้วย น้องๆสามารถดูเนื้อหาได้ที่ >>ความยาวส่วนโค้งของวงกลมหนึ่งหน่วย<<

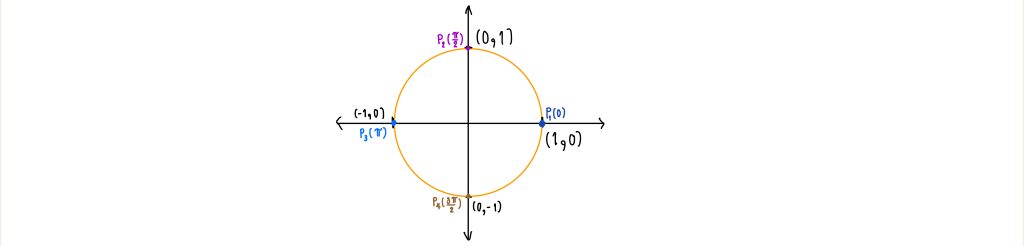
กำหนดให้ P(θ) = (x, y) และ x = cosθ , y = sinθ

พิจารณา θ = 0 จะได้ว่า พิกัดจุดของ P(0) คือ (1, 0) นั่นคือ P(0) = (1, 0)

ดังนั้น x = 1 และ y = 0 นั่นคือ cos(0) = 1 และ sin(0) = 0

พิจารณาที่ θ = $\frac{\pi }{2}$ จะได้ว่า P( $\frac{\pi }{2}$ ) = (0, 1)

ดังนั้น cos( $\frac{\pi }{2}$ ) = 0 และ sin( $\frac{\pi }{2}$ ) = 1

พิจารณา θ = $\pi$ จะได้ว่า P( $\pi$ ) = (-1, 0)

ดังนั้น cos( $\pi$ ) = -1 และ sin( $\pi$ ) = 0

พิจารณาที่ θ = $\frac{3\pi }{2}$ จะได้ว่า P( $\frac{3\pi }{2}$ ) = (0, -1)

ดังนั้น cos( $\frac{3\pi }{2}$ ) = 0 และ cos( $\frac{3\pi }{2}$ ) = -1

การหาค่า sinθ cosθ โดยใช้มือซ้าย

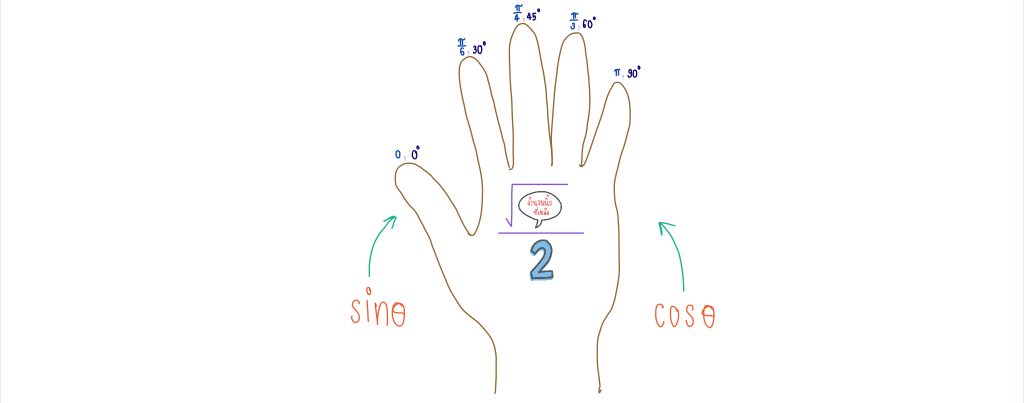
แต่ละนิ้วจะแทนค่าของ θ ดังรูป
เราจะหาค่าโดยการพับนิ้ว เช่น ต้องการหา sin( $\frac{\pi }{3}$ ) เราก็จะพับนิ้วนางลง
เราจะให้นิ้วที่พับลงเป็นตัวแบ่งระหว่าง cos กับ sin ซึ่งจะแบ่งออกเป็นฝั่งซ้ายและฝั่งขวา
ช่องว่างในรูทคือ จำนวนนิ้วที่เรานับได้เมื่อเราพับนิ้วลง
หากต้องการค่า sin ให้นำจำนวนนิ้วฝั่งซ้ายมาเติมในรูท
และหากต้องการค่า cos ให้นำจำนวนนิ้วฝั่งขวามาเติมในรูท

หากน้องๆยังงงๆเรามาดูตัวอย่างกันค่ะ

ต้องการหาค่า cos( $\frac{\pi }{4}$ ) และ sin( $\frac{\pi }{6}$ )

cos( $\frac{\pi }{4}$ )

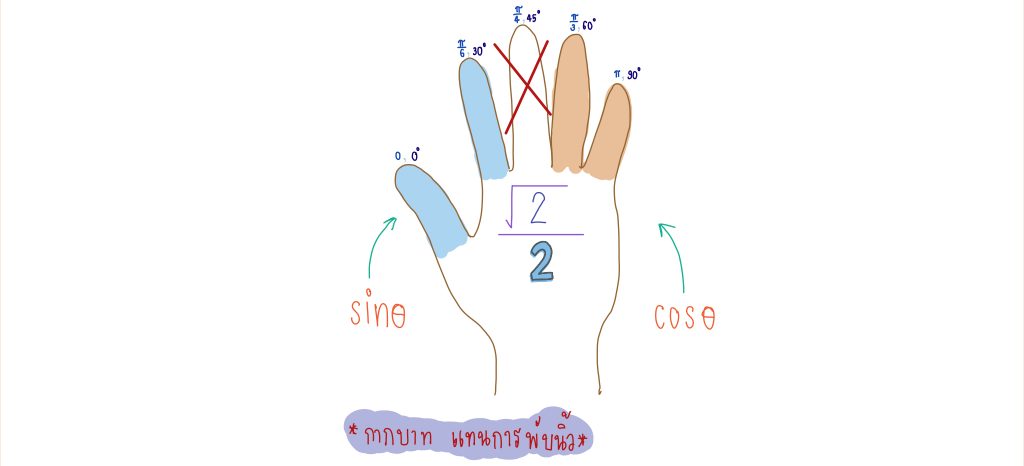
จากโจทย์เราต้องการหาค่าโคไซน์ ที่ θ = $\frac{\pi }{4}$ ซึ่งตรงกับนิ้วกลาง

ดังนั้นเราจึงพับนิ้วกลางลง และหาค่าโคไซน์เราต้องดูจำนวนนิ้วฝั่งขวาซึ่งก็คือนิ้วที่ถูกระบายด้วยสีส้ม จะเห็นว่ามี 2 นิ้ว ดังนั้น cos( $\frac{\pi }{4}$ ) = $\frac{\sqrt{2}}{2}$

sin( $\frac{\pi }{6}$ )

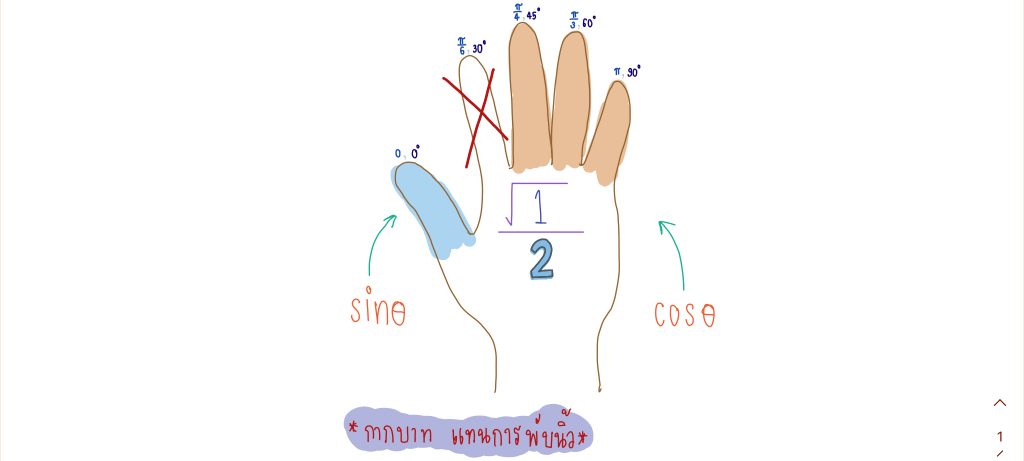
จากโจทย์ต้องการหาค่าฟังก์ชันไซน์ ที่ θ = $\frac{\pi }{6}$ เราจึงพับนิ้วชี้ลง และดูจำนวนนิ้วฝั่งซ้ายซึ่งก็คือนิ้วที่ถูกทาด้วยสีฟ้า ดังนั้น sin( $\frac{\pi }{6}$ ) = $\frac{1}{2}$

แล้วสมมติว่า θ เป็นค่าอื่นๆนอกเหนือจากค่าเหล่านี้ล่ะ เช่น $\frac{2\pi }{3}$ เราจะหายังไงดี???

จริงๆแล้วค่าของ $\frac{2\pi }{3}$ นั้นเราสามารถดูของ $\frac{\pi }{3}$ ได้เลย แต่!!!! เครื่องหมายอาจจะต่างกัน ให้น้องๆสังเกตว่า ค่าของ $\frac{2\pi }{3}$ นั้นอยู่ควอดรันต์ที่เท่าไหร่ แล้วน้องจะรู้ว่าค่า x ควรเป็นลบหรือเป็นบวก ค่า y ควรเป็นลบหรือเป็นบวก

อย่างเช่น cos( $\frac{2\pi }{3}$ )

เรามาดูกันว่า θ = $\frac{2\pi }{3}$ อยู่ควอดรันต์เท่าไหร่

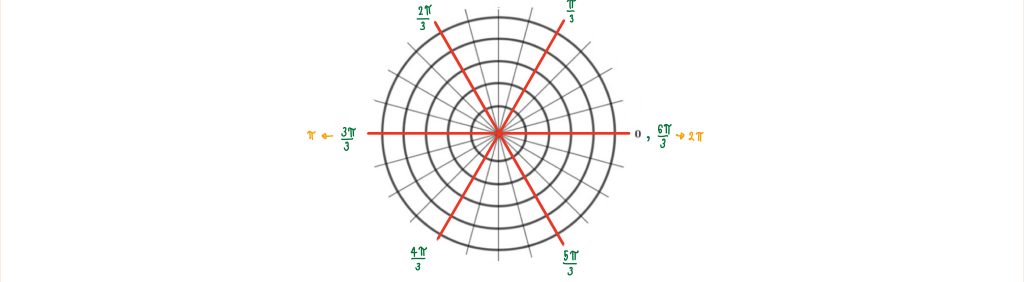
จะเห็นว่าอยู่ควอดรันต์ที่ 2 ซึ่ง (- , +) ดังนั้น ค่า x เป็นจำนวนลบ ค่า y เป็นจำนวนบวก และเรารู้ว่า x = cosθ ดังนั้น ค่า cos( $\frac{2\pi }{3}$ ) เป็นจำนวนลบแน่นอน

จากนั้นใช้มือซ้ายเพื่อหาค่า cos โดยใช้ค่า θ = $\frac{\pi }{3}$ ได้เลย จะได้ว่า cos( $\frac{\pi }{3}$ ) = $\frac{1}{2}$

ดังนั้น cos( $\frac{2\pi }{3}$ ) = $-\frac{1}{2}$

นอกจากจะดูหาค่าโดยใช้มือซ้ายแล้ว น้องๆสามารถดูตามรูปด้านล่างนี้ได้เลยค่ะ

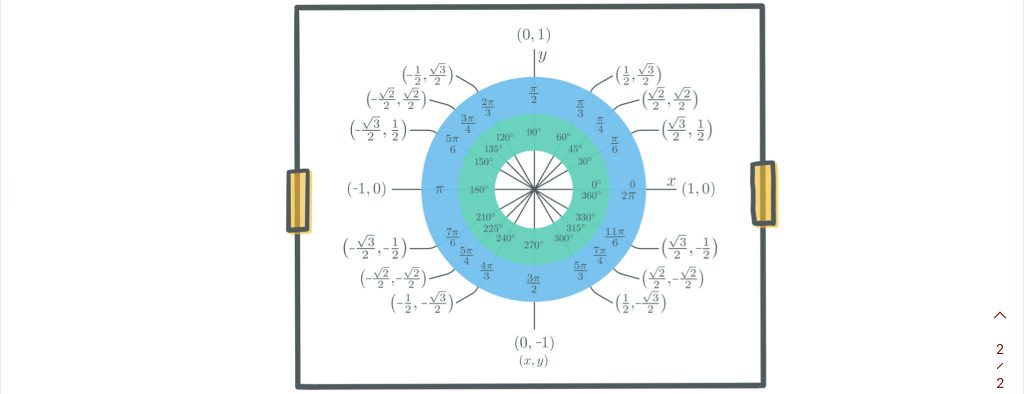
ในวงกลมที่ระบายสีฟ้านั้น คือค่าของ θ ซึ่งแต่ละ θ ก็จะบอกพิกัดจุด (x, y) ซึ่งก็คือค่าของ cosθ และ sinθ นั่นเอง

เช่น sin( $\frac{5\pi }{6}$ ) = $\frac{1}{2}$ และ cos( $\frac{5\pi }{6}$ ) = $-\frac{\sqrt{3}}{2}$

ตัวอย่างการหาค่าฟังก์ชันไซน์และโคไซน์

1) หาค่า sin( $\frac{7\pi }{6}$ )

วิธีทำ หาค่า sin( $\frac{\pi }{6}$ )

จะได้ว่า sin( $\frac{\pi }{6}$ ) = $\frac{1}{2}$

จากนั้นดูพิกัดจุดของ P( $\frac{7\pi }{6}$ ) จะได้ว่า อยู่ควอดรันต์ที่ 3 ซึ่ง (- , -) นั่นคือ ค่า x เป็นจำนวนลบ (cosθ เป็นจำนวนลบ) และค่า y เป็นจำนวนลบ

และจาก y = sinθ

ดังนั้น sin( $\frac{7\pi }{6}$ ) = $-\frac{1}{2}$

2) หาค่า sin²( $\frac{\pi }{6}$ ) + cos²( $\frac{\pi }{6}$ )

วิธีทำ จากความสัมพันธ์ของไซน์และโคไซน์ sin²θ + cos²θ = 1

จะได้ว่าค่าของ sin²( $\frac{\pi }{6}$ ) + cos²( $\frac{\pi }{6}$ ) = 1

เนื่องจากว่าเราเรียนคณิตศาสตร์เราจะต้องไม่เชื่ออะไรง่ายๆ ดังนั้นเราจะมาหาค่าโดยใช้วิธีตรงกันค่ะ

จาก sin( $\frac{\pi }{6}$ ) = $\frac{1}{2}$ จะได้ว่า sin²( $\frac{\pi }{6}$ ) = $\frac{1}{4}$ และ cos( $\frac{\pi }{6}$ ) = $\frac{\sqrt{3}}{2}$ จะได้ว่า cos²( $\frac{\pi }{6}$ ) = $\frac{3}{4}$

ดังนั้น $\frac{1}{4}$ + $\frac{3}{4}$ = $\frac{4}{4}$ = 1

ดังนั้น สรุปได้ว่า sin²( $\frac{\pi }{6}$ ) + cos²( $\frac{\pi }{6}$ ) = 1

3) หาค่า cos²( $\frac{\pi }{2}$ ) + cos²( $\frac{3\pi }{2}$ ) – cos²( $\pi$ )

วิธีทำ จาก cos( $\frac{\pi }{2}$ ) = 0 cos( $\frac{3\pi }{2}$ ) = 0 และ cos( $\pi$ ) = -1

จะได้ว่า cos²( $\frac{\pi }{2}$ ) = 0 cos²( $\frac{3\pi }{2}$ ) = 0 และ cos²( $\pi$ ) = (-1)² = 1

ดังนั้น cos²( $\frac{\pi }{2}$ ) + cos²( $\frac{3\pi }{2}$ ) – cos²( $\pi$ ) = 0 + 0 – 1 = -1

น้องๆสามารถหาแบบฝึกหัดมาทำเพิ่มเติมโดยใช้กฎมือซ้ายในการช่วยหาค่าฟังก์ชันแต่ทั้งนี้น้องๆก็ต้องมีพื้นฐานเกี่ยวกับความยาวจุดปลายส่วนโค้งด้วยนะคะ และการหาค่าฟังก์นั้นนี้หากน้องๆทำบ่อยจะทำให้น้องจำได้ และเวลาสอบก็จะช่วยให้ทำข้อสอบได้เร็วยิ่งขึ้นด้วยค่ะ

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

เรียนรู้ตัวบทเด่นของบทละครพูดคำฉันท์เรื่องดัง มัทนะพาธา

มัทนะพาธา เป็นบทละครพูดคำฉันท์ที่ประพันธ์โดยรัชกาลที่ 6 ซึ่งพระองค์ทรงคิดขึ้นเองไม่ได้แปลหรือดัดแปลงมาจากเรื่องใด จากการศึกษาความเป็นมาในบทเรียนคราวที่แล้วทำให้เราได้รู้ที่มา ลักษณะคำประพันธ์รวมไปถึงเรื่องย่อของเรื่องกันไปแล้ว บทเรียนในวันนี้เราจะศึกษาตัวบทเด่น ๆ ของเรื่องกันนะคะว่ามีบทใดที่ได้ชื่อว่าเป็นวรรคทอง ถอดความ พร้อมทั้งเรียนรู้คุณค่าของานประพันธ์ชิ้นนี้อีกด้วย ถ้าน้อง ๆ อยากรู้แล้วเราไปเรียนรู้เรื่องนี้พร้อมกันเลยค่ะ ตัวบทเด่น ๆ ใน มัทนะพาธา ถอดความ บทนี้เป็นคำพูดของฤษีกาละทรรศินที่กำลังอธิบายให้ศุภางค์ แม่ทัพของท้าวชัยเสนว่าเหตุใดพระฤษีจึงเห็นว่าการห้ามปรามความรักระหว่างพระชัยเสนกับมัทนาเป็นสิ่งไร้ประโยชน์ โดยบอกว่า

พื้นที่ผิวของปริซึมและทรงกระบอก

เราได้หาปริมาตรของรูปเรขาคณิตสามมิติต่าง ๆ มาบ้างแล้ว ในหัวข้อนี้จะกล่าวถึงการหาพื้นที่ผิวของปริซึมและทรงกระบอก

ลำดับเลขคณิต

ลำดับเลขคณิต ลำดับเลขคณิต คือลำดับที่มีค่าเพิ่มขึ้นหรือลดลงอย่างคงที่ โดยจำนวนที่เพิ่มขึ้นหรือลดลงนี้เราเรียกว่าผลต่างร่วม แทนด้วยสัญลักษณ์ d โดยที่ d = พจน์ขวา – พจน์ซ้าย การเขียนลำดับเราจะเขียนแทนด้วย โดยที่ คือพจน์ทั่วไปหรือเรียกอีกอย่างว่า พจน์สุดท้ายนั่นเอง การหาพจน์ทั่วไปของลำดับเลขคณิต พจน์ที่1 n = 1

โจทย์ปัญหาเกี่ยวกับ ห.ร.ม. และ ค.ร.น.

บทความนี้เป็นเรื่องการแก้ โจทย์ปัญหาเกี่ยวกับ ห.ร.ม. และ ค.ร.น ซึ่งโจทย์ที่ได้นำมาเป็นตัวอย่างจะประกอบด้วยการวิเคราะห์โจทย์ปัญหา การเลือกใช้วิธีการแก้โจทย์ปัญหา รวมไปถึงการแสดงวิธีทำอย่างละเอียด หวังว่าน้องๆจะสามารถนำข้อมูลเหล่านี้ไปใช้ได้จริงกับโจทย์ปัญหาในห้องเรียน ซึงเป็นเเรื่องย่อยของ ห.ร.ม. และ ค.ร.น. ป.6

การใช้ Possessive Pronoun

สวัสดีค่ะนักเรียนชั้นป.6 ที่น่ารักทุกคน วันนี้เราจะไปเรียนรู้เรื่อง การใช้ Possessive Pronoun ถ้าพร้อมแล้วก็ไปลุยกันเลยจ้า บทนำ Possessive pronoun (เช่น mine, yours, hers) ถือเป็นหัวข้อหนึ่งในภาษาอังกฤษที่หลายคนมักจะสับสน นั่นก็เพราะมันมีความคล้ายคลึงกับ Possessive adjective (เช่น my, your, her) ลองเปรียบเทียบประโยคเหล่านี้ดูนะคะ A

คำเชื่อมในภาษาอังกฤษ (Conjunctions)

สวัสดีค่ะนักเรียนชั้นม.4 ที่รักทุกคนวันนี้เราจะไปเรียนรู้กันเรื่อง “คำเชื่อมในภาษาอังกฤษ หรือ Conjunctions” กันนะคะ ถ้าพร้อมแล้วก็ไปลุยกันโลด ความหมาย Conjunctions คือ คำที่ใช้เชื่อมระหว่างประโยคต่อประโยค คำต่อคำ หรือระหว่างกริยาต่อกริยา และอื่นๆ ดังตัวอย่างด้านล่างเลยจ้า ตัวอย่างเช่น เชื่อมนามกับนาม Time and tide wait for no man. เวลาและวารีไม่เคยรอใคร

ค่าของฟังก์ชันไซน์และโคไซน์

สารบัญ

ค่าของฟังก์ชันไซน์และโคไซน์

โดเมนและเรนจ์ของ sine function และ cosine function

ความสัมพันธ์ของฟังก์ชันไซน์และโคไซน์

การหา ค่าของฟังก์ชันไซน์และโคไซน์

การหาค่า sinθ cosθ โดยใช้มือซ้าย

ตัวอย่างการหาค่าฟังก์ชันไซน์และโคไซน์

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

เรียนรู้ตัวบทเด่นของบทละครพูดคำฉันท์เรื่องดัง มัทนะพาธา

พื้นที่ผิวของปริซึมและทรงกระบอก

ลำดับเลขคณิต

โจทย์ปัญหาเกี่ยวกับ ห.ร.ม. และ ค.ร.น.

การใช้ Possessive Pronoun

คำเชื่อมในภาษาอังกฤษ (Conjunctions)

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1