ตัวหารร่วมมาก (ห.ร.ม.)
ตัวหารร่วมมาก (ห.ร.ม.) ของจำนวนนับตั้งแต่สองจำนวนขึ้นไปนั้น เป็นการหาตัวหารร่วมหรือตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับเหล่านั้น ในบทความนี้ได้รวบรวมวิธี การหา ห.ร.ม. ไว้ทั้งหมด 3 วิธี น้องๆอาจคุ้นชินกับ การหา ห.ร.ม. โดยวิธีตั้งหาร แต่น้องๆทราบหรือไม่ว่าวิธีการหา ห.ร.ม. มีวิธีการดังต่อไปนี้
- การหา ห.ร.ม. โดยการหาผลคูณร่วม
- การหา ห.ร.ม. โดยการแยกตัวประกอบ
- การหา ห.ร.ม. โดยการหาร (หารสั้น)
ก่อนที่น้องจะไปศึกษาวิธีการหา ห.ร.ม. นั้น น้องๆ มาดูบทนิยามของ ตัวหารร่วมหรือตัวประกอบร่วม กันก่อนนะคะ
ตัวหารร่วม หรือ ตัวประกอบร่วม ของจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนนับใด ๆ ที่หารจำนวนนับเหล่านั้นได้ลงตัวทุกจำนวน
น้องๆ ทราบหรือไม่ว่า ตัวประกอบของทั้งหมดของ 45 และ 90 มีจำนวนใดบ้าง
ตัวประกอบทั้งหมดของ 45 คือ 1, 3, 5, 9, 15, 45
ตัวประกอบทั้งหมดของ 90 คือ 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
พิจารณาตัวประกอบของ 45 และ 90 ว่าจำนวนใดบ้างที่สามารถหารทั้ง 45 และ 90 ได้ลงตัว จะได้ว่า จำนวนนั้นคือ 1, 3, 5, 9, 15, 45
ต่อไปมาศึกษาวิธีการหารร่วมหรือตัวประกอบร่วม กันนะคะ
ตัวอย่างที่ 1 จงหาตัวหารร่วมหรือตัวประกอบร่วมของ 10 และ 12
วิธีทำ ตัวหารร่วมหรือตัวประกอบร่วมของ 10 และ 12 สามารถหาได้ ดังนี้
ตัวประกอบทั้งหมดของ 10 คือ 1, 2, 5, 10
ตัวประกอบทั้งหมดของ 12 คือ 1, 2, 3, 4, 6, 12
ดังนั้น ตัวหารร่วมหรือตัวประกอบร่วมของ 10 และ 12 คือ 1 และ 2
ตัวอย่างที่ 2 จงหาตัวหารร่วมหรือตัวประกอบร่วมของ 12, 15 และ 18
วิธีทำ ตัวหารร่วมหรือตัวประกอบร่วมของ 12, 15 และ 18 สามารถหาได้ ดังนี้
ตัวประกอบทั้งหมดของ 12 คือ 1, 2, 3, 4, 6, 12
ตัวประกอบทั้งหมดของ 15 คือ 1, 3, 5, 15
ตัวประกอบทั้งหมดของ 18 คือ 1, 2,3, 6, 9, 18
ดังนั้น ตัวหารร่วมหรือตัวประกอบร่วมของ 12, 15 และ 18 คือ 1 และ 3
ข้อสังเกต เนื่องจาก 1 หารจำนวนนับทุกจำนวนลงตัว ดังนั้น 1 เป็นตัวหารร่วมหรือตัวประกอบร่วมของจำนวนนับทุกจำนวน
เมื่อน้องๆเข้าใจ ตัวหารร่วม หรือ ตัวประกอบร่วม กันดีแล้ว ลำดับต่อไปขอนำเสนอ บทนิยาม ตัวหารร่วมมาก (ห.ร.ม.) ดังนี้
ตัวหารร่วมมาก (ห.ร.ม.) ของจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป หมายถึง ตัวหารร่วมหรือตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับเหล่านั้น
เมื่อน้องๆ เข้าใจบทนิยามของ ตัวหารร่วมมาก (ห.ร.ม.) ลำดับต่อไป จะนำเสนอวิธีการหา ห.ร.ม. ทั้ง 3 วิธีกันคะ มาเริ่มทีวิธีแรกกันเลยนะคะ
วิธีที่ 1 การหา ห.ร.ม. โดยการหาผลคูณร่วม
หลักการ
- หาตัวหารหรือตัวประกอบทั้งหมดของจำนวนนับที่ต้องการหา ห.ร.ม. แต่ละจำนวน
- พิจารณาตัวหารร่วม หรือตัวประกอบร่วมที่มีค่ามากที่สุด
- ห.ร.ม. คือ ตัวหารร่วม หรือตัวประกอบร่วมที่มีค่ามากที่สุด
เมื่อศึกษาหลักการหา ห.ร.ม. โดยการหาผลคูณร่วม เรียบร้อยแล้ว น้องๆมาศึกษาตัวอย่างได้เลยคะ
ตัวอย่างที่ 3 จงหา ห.ร.ม. ของ 12, 18, และ 24 โดยการพิจารณาตัวประกอบ
วิธีทำ ตัวประกอบทั้งหมดของ 12 คือ 1, 2, 3, 4, 6 และ 12
ตัวประกอบทั้งหมดของ 18 คือ 1, 2, 3, 6, 9 และ 18
ตัวประกอบทั้งหมดของ 24 คือ 1, 2, 3, 4, 6, 8, 12 และ 24
จะได้ว่า ตัวประกอบร่วมของ 12, 18, และ 24 คือ 1, 2, 3 และ 6
ตัวประกอบร่วมที่มากที่สุดของ 12, 18 และ 24 คือ 6
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 12, 18 และ 24 คือ 6
ตัวอย่างที่ 4 จงหา ห.ร.ม. ของ 18, 27 และ 36 โดยการพิจารณาตัวประกอบ
วิธีทำ ตัวประกอบทั้งหมดของ 18 คือ 1, 2, 3, 6, 9 และ 18
ตัวประกอบทั้งหมดของ 27 คือ 1, 3, 9 และ 27
ตัวประกอบทั้งหมดของ 36 คือ 1, 2, 3, 4, 6, 9, 12, 18 และ 36
จะได้ว่า ตัวประกอบร่วมของ 18, 27 และ 36 คือ 1, 3 และ 9
ตัวประกอบร่วมที่มากที่สุดของ 18, 27 และ 36 คือ 9
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 18, 27 และ 36 คือ 9
การหา ห.ร.ม. โดยใช้วิธีที่ 1 จะเป็นการหาตัวประกอบร่วมที่มีค่ามากที่สุด ต่อไปน้องๆมาศึกษาวิธี การหา ห.ร.ม. โดยการแยกตัวประกอบ ได้เลยคะ
วิธีที่ 2 การหา ห.ร.ม. โดยการแยกตัวประกอบ
- แยกตัวประกอบทั้งหมดของจำนวนนับที่ต้องการหา ห.ร.ม. แต่ละจำนวน
- พิจารณาตัวประกอบเฉพาะที่ซ้ำกันทุกจำนวน
- ห.ร.ม. คือผลคูณของตัวประกอบเฉพาะดังกล่าว
เมื่อศึกษาหลักการหา ห.ร.ม. โดยการแยกตัวประกอบ เรียบร้อยแล้ว น้องๆมาศึกษาตัวอย่างได้เลยคะ
ตัวอย่างที่ 5 จงหา ห.ร.ม. ของ 40, 72 และ 104 โดยการแยกตัวประกอบ
วิธีทำ การแยกตัวประกอบของ 40, 72 และ 104 ทำได้ดังนี้
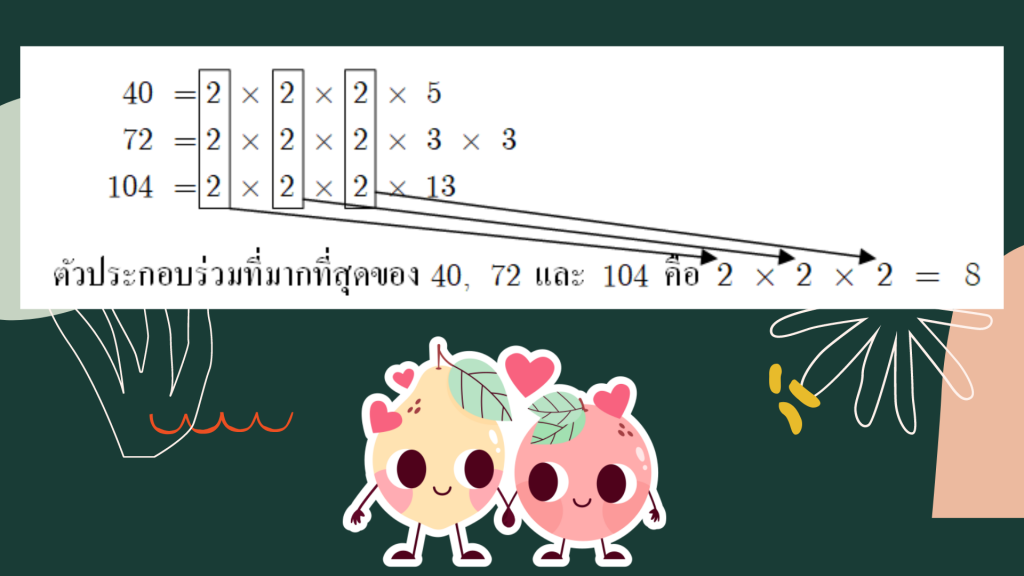
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 40, 72 และ 104 คือ 8
ตัวอย่างที่ 6 จงหา ห.ร.ม. ของ 108, 180 และ 228 โดยการแยกตัวประกอบ
วิธีทำ การแยกตัวประกอบของ 108, 180 และ 228 ทำได้ดังนี้
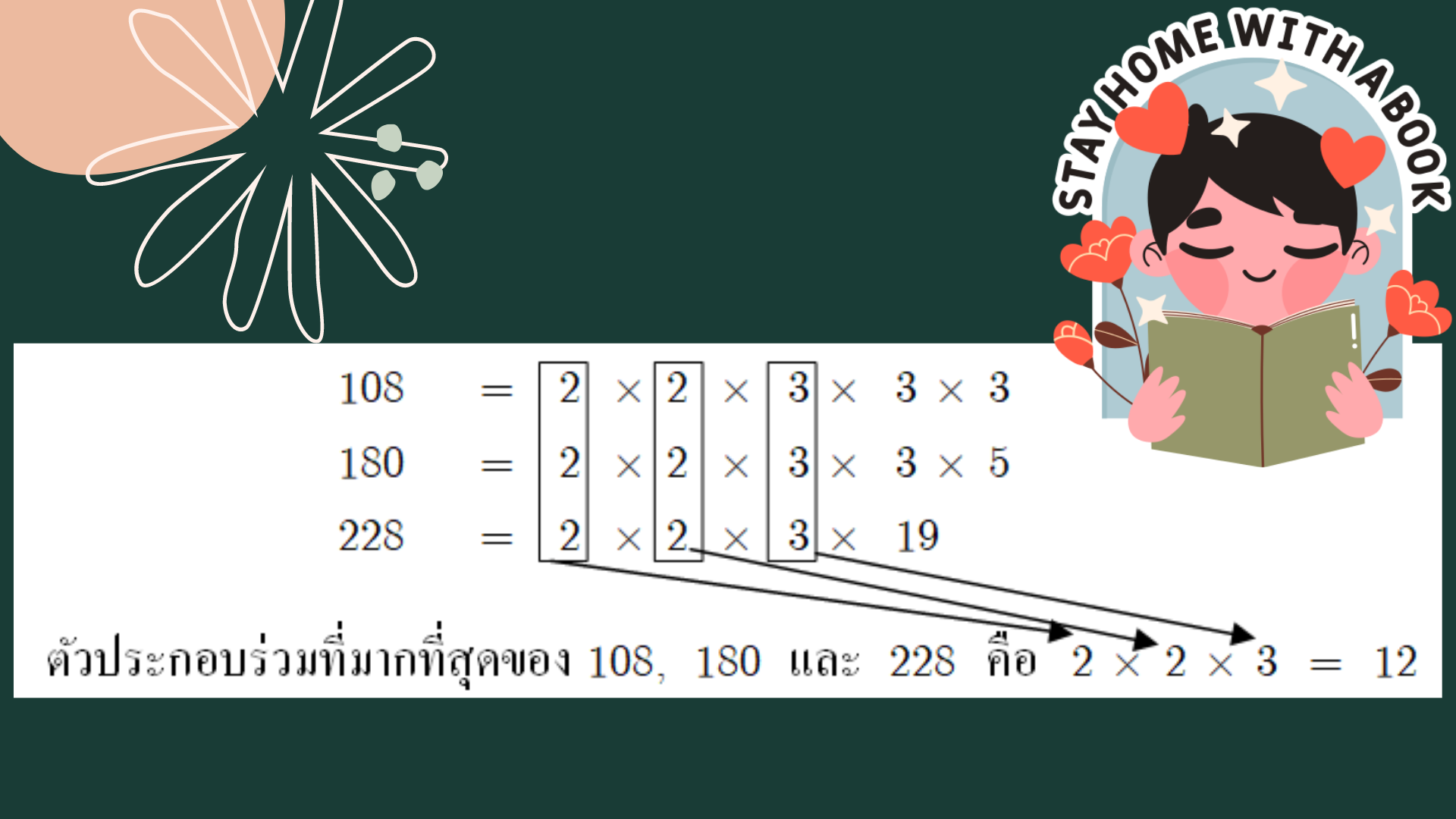
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 108, 180 และ 228 คือ 12
หมายเหตุ : การหา ห.ร.ม. ของจำนวนนับ 3 จำนวนใดๆ จะต้องมี 3 จำนวนซ้ำกัน ซึ่งจะต้องเอาจำนวนที่ซ้ำกันมา 1 ตัว มาคูณกัน ดังตัวอย่างข้างต้น
จะดีกว่ามั้ยคะ ถ้ามีวิธีการที่จะสามารถหา ห.ร.ม. ได้รวดเร็วยิ่งขึ้น แต่ทั้งนี้ทั้งนั้นขึ้นอยู่กับความถนัดของแต่ละบุคคลนะคะ น้องๆ ลองศึกษาวิธีสุดท้ายได้โดยใช้วิธีที่ 1 ง่ายมากเลยใช่มั้ยค่ะ ต่อไปน้องๆ มาศึกษาวิธี การหา ห.ร.ม. โดยการแยกตัวประกอบ ได้เลยคะ
วิธีที่ 3 การหา ค.ร.น. โดยการหาร (หารสั้น)
หลักการ
- หาจำนวนเฉพาะที่หารทุกจำนวนได้ลงตัว
- หาจำนวนเฉพาะที่หารผลลัพธ์ทุกตัวได้ลงตัว ดำเนินการเช่นนี้ไปเรื่อย ๆ จนไม่มีจำนวนเฉพาะใดหารผลลัพธ์ทุกตัวได้ลงตัว
- ห.ร.ม. คือ ผลคูณของจำนวนเฉพาะที่นำไปหารในแต่ละขั้นตอน
เมื่อศึกษาหลักการหา ห.ร.ม. โดยการหาร (หารสั้น) เรียบร้อยแล้ว น้องๆมาศึกษาตัวอย่างได้เลยคะ
ตัวอย่างที่ 7 จงหา ห.ร.ม. ของ 168 และ 264 โดยวิธีตั้งหารสั้น
วิธีทำ
2 )168 264
2 ) 84 132
2 ) 42 66
3 ) 21 33
7 11
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 168 และ 264 คือ 2 x 2 x 2 x 3 = 24
ตัวอย่างที่ 8 จงหา ห.ร.ม. ของ 24 , 60 และ 84 โดยการตั้งหาร
วิธีทำ
2 ) 24 60 84
2 ) 12 30 42
3 ) 6 15 21
2 5 7
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 24, 60 และ 84 คือ 2 x 2 x 3 = 12
ตัวอย่างที่ 9 จงหา ห.ร.ม. ของ 18, 27 และ 36
วิธีทำ
3 )18 27 36
3 ) 6 9 12
2 3 4
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 18, 27 และ 36 คือ 3 x 3 = 9
ตัวอย่างที่ 10 จงหา ห.ร.ม. ของ 40, 72 และ 104 โดยการตั้งหาร
วิธีทำ
2 ) 40 72 104
2 ) 20 36 52
2 ) 10 18 26
5 9 13
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 40, 72 และ 104 คือ 2 x 2 x 2 = 8
ตัวอย่างที่ 11 จงหา ห.ร.ม. ของ 72, 144 และ 216 โดยการตั้งหาร
วิธีทำ
2 ) 72 144 216
2 ) 36 72 108
2 ) 18 36 54
3 ) 9 18 27
3 ) 3 6 9
1 2 3
ดังนั้น ตัวหารร่วมมาก (ห.ร.ม.) ของ 72, 144 และ 216 คือ 2 x 2 x 2 x 3 x 3 = 72
เมื่อน้องๆเรียนรู้เรื่อง ตัวหารร่วมมาก (ห.ร.ม.) จาก ตัวอย่าง ห.ร.ม. หลายๆตัวอย่าง จะเห็นได้ชัดว่า การหา ห.ร.ม. ไม่ได้เป็นเรื่องยากอย่างที่คิด ลำดับต่อไปที่น้องๆต้องเรียนรู้คือการหา ตัวคูณร่วมน้อย (ค.ร.น.) ซึ่งจะเป็นการฝึกน้องๆได้มีวิธีการหา ค.ร.น. แต่ละข้อได้อย่างรวดเร็วและแม่นยำ
คลิปวิดีโอ การหา ห.ร.ม.
คลิปวิดีโอนี้ได้รวบรวมวิธีการหา ตัวหารร่วมมาก (ห.ร.ม.) ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค การหา ห.ร.ม. รวมถึงการอธิบาย ตัวอย่าง และสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย



















