สัญลักษณ์แทนการบวก

supanaree

คณิตศาสตร์, ม.6, ลำดับและอนุกรม

Add LINE friends for one click to find article.

สัญลักษณ์แทนการบวก

สัญลักษณ์แทนการบวก หรือ $\Sigma$ เรียกว่า ซิกมา ( Sigma ) เราใช้เพื่อลดรูปการบวกกันของตัวเลข เนื่องจากว่าบางทีเป็นการบวกของจำนวนตัวเลข 100 พจน์ ถ้ามานั่งเขียนทีละตัวก็คงจะเยอะไป เราจึงจะใช้เครื่องหมายซิกมามาใช้เพื่อประหยัดเวลาในการเขียนนั่นเอง

เช่น 1 + 2 + 3 + 4 +5 สามารถเขียนแทนด้วย $สัญลักษณ์แทนการบวก$

1 + 1 + 1 + 1 + 1 + 1 สามารถเขียนแทนด้วย $\sum_{i=1}^{6}1$

สูตรผลร่วม

สูตรเหล่านี้จะทำให้น้องๆประหยัดเวลาในการทำโจทย์มากๆ เนื่องจากไม่ต้องมานั่งแทน n ทีละตัว แล้วนำมาบวกกัน แต่สามารถใช้สูตรนี้ในการหาผลรวมได้เลย ดังนั้นจำสูตรเหล่านี้ไว้ดีๆนะคะ

$สัญลักษณ์แทนการบวก$

$\sum_{i=1}^{n}i^{3}=(\frac{n(n+1)}{6})^{2}$

***สูตรข้างต้นใช้ได้กับการบวกตั้งแต่ 1 ถึง n เท่านั้น***

สมบัติที่ควรรู้เกี่ยวกับ 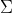$\Sigma$

สมบัติเหล่านี้จะช่วยให้น้องๆคิดเลขได้ง่ายขึ้นและประหยัดเวลาในการทำโจทย์แต่ละข้อได้เยอะมากๆ

ให้ $a_n,b_n$ เป็นลำดับของจำนวนจริงใดๆ

1) $\sum_{n=1}^{k}c=kc$ โดยที่ c เป็นค่าคงที่ใดๆ

2) $สัญลักษณ์แทนการบวก$

3) $สัญลักษณ์แทนการบวก$

4) $\sum ca_n=c\sum a_n$ โดยที่ c เป็นจำนวนจริงใดๆ

ตัวอย่างเกี่ยวกับสัญลักษณ์การบวก

1)จงหาค่าของ $\sum_{n=1}^{4}5$

วิธีทำ จากโจทย์เราจะใช้สมบัติของซิกมาข้อที่ 1 เนื่องจาก 5 เป็นค่าคงที่ $สัญลักษณ์แทนการบวก$

ดังนั้นจะได้ว่า $\sum_{n=1}^{4}5=4(5)=20$

2) จงหาค่าของ $\sum_{n=1}^{50}(-1)$

วิธีทำ ใช้สมบัติข้อที่ 1 เนื่องจาก -1 เป็นค่าคงที่ $\sum_{n=1}^{k}c=kc$ จะได้

$สัญลักษณ์แทนการบวก$

3) ถ้า $a_1+a_2+a_3+a_4=35$ จงหาค่า $\sum_{n=1}^{4}5a_n$

วิธีทำ จากโจทย์จะเห็นว่า $สัญลักษณ์แทนการบวก$

พิจารณา $\sum_{n=1}^{4}5a_n$ โดยใช้สมบัติข้อที่ 4 $\sum ca_n=c\sum a_n$

ดังนั้นจะได้ $\sum_{n=1}^{4}5a_n=5\sum_{n=1}^{4}a_n$ และเนื่องจากเรารู้ว่า $a_1+a_2+a_3+a_4=\sum_{n=1}^{4}a_n=35$

ดังนั้น $\sum_{n=1}^{4}5a_n=5\sum_{n=1}^{4}a_n=5(35)=175$

4) ให้ $\sum_{n=1}^{10}a_n=55, \sum_{n=1}^{10}b_n=27,\sum_{n=1}^{10}c_n=-22$ จงหา $\sum_{n=1}^{10}[5a_n-2b_n-6c_n]$

วิธีทำ เราจะพิจารณาสิ่งที่โจทย์ถามก่อน นั่นก็คือ $\sum_{n=1}^{10}[5a_n-2b_n-6c_n]$ เราจะเห็นว่าในวงเล็บนั้นเป็นลำดับที่กำลังลบกันอยู่และจากสมบัติของซิกมาเราสามารถกระจายซิกมาเข้าไปได้(สมบัติข้อที่ 3) จะได้ว่า

$สัญลักษณ์แทนการบวก$

และจากสมบัติข้อที่ 4 เราสามารถดึงข้าคงที่ออกมาไว้ข้างนอกซิกมาได้ จะได้ว่า

$\sum_{n=1}^{10}5a_n-\sum_{n=1}^{10}2b_n-\sum_{n=1}^{10}6c_n=5\sum_{n=1}^{10}a_n-2\sum_{n=1}^{10}b_n-6\sum_{n=1}^{10}c_n$

จะเห็นว่าเราสามารถตอบได้แล้ว เพราะเราสามารถเอาสิ่งที่โจทย์กำหนดให้มาแทนค่าลงไปได้แล้วจะได้เป็น

$5\sum_{n=1}^{10}a_n-2\sum_{n=1}^{10}b_n-6\sum_{n=1}^{10}c_n=5(55)-2(27)-6(-22)=353$

ดังนั้น $\sum_{n=1}^{10}[5a_n-2b_n-6c_n]=353$

5) จงหาผลบวกของ 1 + 2 + 3 + 4 +…+ 64

วิธีทำ จากโจทย์เป็นการบวกกันของจำนวนนับตั้งแต่ 1 ถึง 64 และเราสามารถเขียน 1 + 2 + 3 + 4 +…+ 64 ให้อยู่ในรูปของซิกมาได้ จะได้ว่า

1 + 2 + 3 + 4 +…+ 64 = $\sum_{i=1}^{64}i$

และจากสูตร $สัญลักษณ์แทนการบวก$ ในโจทย์ข้อนี้ n = 64 ดังนั้นจะได้ว่า

$สัญลักษณ์แทนการบวก$

ดังนั้น 1 + 2 + 3 + 4 +…+ 64 = 2,080

6) จงหาผลบวกของ $1^2+2^2+3^2+...+10^2$

วิธีทำ จากโจทย์เป็นการบวกของกำลังสองของจำนวนนับตั้งแต่ 1 ถึง 10 และเราสามารถเขียน $1^2+2^2+3^2+...+10^2$ ให้อยู่ในรูปของซิกมาได้

จะได้เป็น

$1^2+2^2+3^2+...+10^2=\sum_{i=1}^{10}i^2$

และจากสูตร $สัญลักษณ์แทนการบวก$ เราจะเห็นว่า n = 10 ดังนั้นจะได้

$สัญลักษณ์แทนการบวก$

ดังนั้น $1^2+2^2+3^2+...+10^2$ = 385

สรุป จากตัวอย่างข้างต้นจะเห็นว่าสมบัติของซิกมาและสูตรเกี่ยวกับผลบวกนั้นมีประโยชน์ในการแก้โจทย์อย่างมาก ทำให้ประหยัดเวลาในการคำนวณ และทำให้โจทย์ที่เหมือนจะยากนั้นง่ายขึ้นอีกด้วย ดังนั้นน้องๆอย่าลืมจำสูตรและสมบัติเหล่านี้นะคะ

วิดีโอเกี่ยวกับ สัญลักษณ์แทนการบวก

น้องๆสามารถเรียนรู้เพิ่มเติมเกี่ยวกับซิกมาและสมบัติของซิกมาได้จากคลิปด้านล่างนี้เลยค่ะ

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

Life is Simple: ทำความรู้จัก Present Simple Tense

เรื่อง Tense (กาล) ในภาษาอังกฤษเป็นเรื่องที่สำคัญมากๆ อีกเรื่องหนึ่ง และ Tense ที่เป็นพื้นฐานสุดๆ และน้องๆ จะพบเจอบ่อยที่สุดก็คือ Present Simple นั่นเอง วันนี้เราจะมาปูพื้นฐานและทบทวนความรู้เรื่องนี้กันครับ

Present Perfect Continuous แบบเข้าใจง่ายและใช้ได้จริง

สวัสดีน้องๆ ม. 4 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้เกี่ยวกับ Present Perfect Continuous ในภาษาอังกฤษกันครับ จะเป็นอย่างไรเราไปเริ่มกันเลยดีกว่าครับ

ระดับภาษา เรียนรู้วิธีใช้ให้ถูกต้องและเหมาะสม

ระดับภาษา มีความสำคัญอย่างมากในภาษาไทย น้อง ๆ ทราบไหมคะว่าภาษาที่เราใช้กันอยู่ในทุกวันนี้ ก็มีระดับของมันที่จะเป็นตัวบ่งบอกความเหมาะสม ให้เราได้เลือกใช้กันอย่างถูกกาลเทศะ อยากรู้ไหมคะว่ามีกี่ระดับ แต่ละระดับเป็นอย่างไร ต้องใช้แบบไหน ใช้กับใครจึงจะถูก ถ้าพร้อมแล้ว ไปเรียนรู้บทเรียนภาษาไทยในวันนี้กันเลยค่ะ ความหมายของ ระดับภาษา ระดับภาษา หมายถึง ความลดหลั่นของถ้อยคำและการเรียบเรียงถ้อยคำที่ใช้โดยพิจารณาตามโอกาสหรือกาลเทศะ ความสัมพันธ์ระหว่างบุคคลที่เป็นผู้สื่อสาร ผู้รับสาร และเนื้อหาที่สื่อสาร

ค่าของฟังก์ชันไซน์และโคไซน์

ค่าของฟังก์ชันไซน์และโคไซน์ ค่าของฟังก์ชันไซน์และโคไซน์ จะเกี่ยวข้องกับ θ พิกัดของ จุด (x, y) ซึ่งในบทความนี้จะอธิบายเกี่ยวกับ ความสัมพันธ์ระหว่าง x, y กับ θ จากบทความที่ผ่านมาเราได้รู้จักวงกลมหนึ่งหน่วยและการวัดความยาวส่วนโค้ง ในบทความนี้น้องๆจะได้รู้จักกับฟังก์ชันไซน์ (sine function) และฟังก์ชันโคไซน์ (cosine function) และวิธีการหาค่าของฟังก์ชันทั้งสอง Sine function =

การถามทางในภาษาอังกฤษ Asking for Direction in English

สวัสดีค่ะนักเรียนป.6 ที่น่ารักทุกคน เคยมั้ยที่เราเจอฝรั่งถามทางแล้วตอบไม่ได้ ทำได้แค่ชี้ๆ แล้วก็บ๊ายบาย หากทุกคนเคยเจอปัญหานี้ ต้องท่องศัพท์และรู้โครงสร้างประโยคที่สำคัญในการถามทางแล้วล่ะ ไปลุยกันเลย การถามทางในภาษาอังกฤษ Asking for Direction in English การถามทิศทางจะต้องมีประโยคเกริ่นก่อนเพื่อให้คนที่เราถาม ตั้งตัวได้ว่า กำลังจะโดนถามอะไร ยังไง ซึ่งเราสามารถถามได้ทั้ง คำถามแบบสุภาพเมื่อพูดกับคนที่เราไม่คุ้นเคย หรือ คำถามทั่วไปเมื่อพูดกับคนใกล้ตัว

การใช้รูปประโยคคำสั่ง คำขอร้อง คำแนะนำ ที่ใช้ในการเรียน + การใช้ Can/ Could/ Should

สวัสดีค่ะนักเรียนชั้นม. 1 ที่น่ารักทุกคน วันนี้ครูจะพาเรียนรู้เกี่ยวกับ การใช้รูปประโยคคำสั่ง คำขอร้อง คำแนะนำ ที่เจอบ่อยและการใช้ Can, Could, Should กันนะคะ ไปลุยกันเลย มารู้จักกับประโยคคำสั่ง (Imperative sentence) รูปแบบและโครงสร้างประโยคคำสั่ง Imperative sentence Imperative sentence ในรูปแบบประโยคบอกเล่าจะ

สัญลักษณ์แทนการบวก

สารบัญ

สัญลักษณ์แทนการบวก

สูตรผลร่วม

สมบัติที่ควรรู้เกี่ยวกับ $\Sigma$

ตัวอย่างเกี่ยวกับสัญลักษณ์การบวก

วิดีโอเกี่ยวกับ สัญลักษณ์แทนการบวก

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

Life is Simple: ทำความรู้จัก Present Simple Tense

Present Perfect Continuous แบบเข้าใจง่ายและใช้ได้จริง

ระดับภาษา เรียนรู้วิธีใช้ให้ถูกต้องและเหมาะสม

ค่าของฟังก์ชันไซน์และโคไซน์

การถามทางในภาษาอังกฤษ Asking for Direction in English

การใช้รูปประโยคคำสั่ง คำขอร้อง คำแนะนำ ที่ใช้ในการเรียน + การใช้ Can/ Could/ Should

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1