ประพจน์ที่สมมูล

ประพจน์ที่สมมูลกัน คือ ประพจน์ที่มีค่าความจริงเหมือนกันทุกกรณี เขียนแทนด้วยสัญลักษณ์ “≡”

แล้วค่าความจริงเหมือนกันทุกกรณี คือยังไง?? เรามาลองพิจารณาค่าความจริงของประพจน์ p→q และ ∼q→∼p จากตารางค่าความจริงกันค่ะ

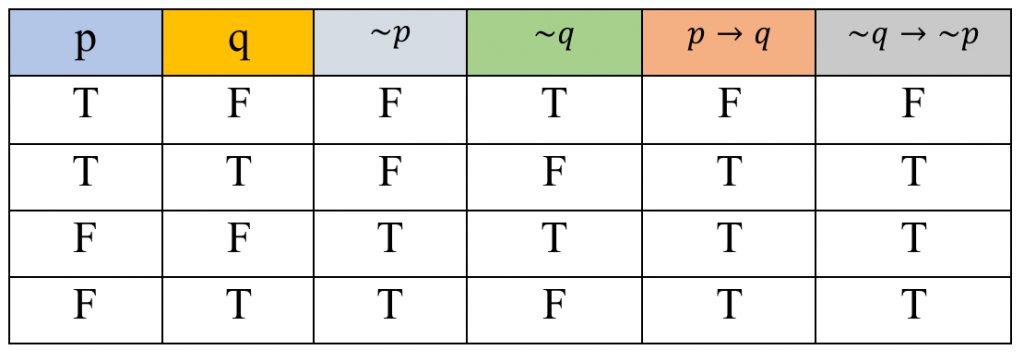
จากตาราง จะเห็นว่า p→q และ ∼q→∼p มีค่าความจริงเหมือนกันทุกกรณี ดังนั้นเราจะได้ว่า p→q และ ∼q→∼p เป็นประพจน์ที่สมมูลกัน เขียนแทนด้วย p→q ≡ ∼q→∼p

หลังจากที่เรารู้แล้วว่าประพจน์ที่สมมูลกันคืออะไร ต่อไปเรามาดูตัวอย่างของประพจน์ที่สมมูลกันค่ะ (ควรจำให้ได้ แล้วจะเป็นประโยชน์มากๆ)

1.) p∧p≡ p

2.) p∨p≡p

3.) (p∨q)∨r ≡ p∨(q∨r) (เปลี่ยนกลุ่ม)

4.) (p∧q)∧r ≡ p∧(q∧r) (เปลี่ยนกลุ่ม)

5.) p∨q ≡ q∨p (สลับที่)

6.) p∧q ≡ p∧q (สลับที่)

7.) p∨(q∧r) ≡ (p∨q)∧(p∨r) (แจกแจง)

8.) p∧(q∨r) ≡ (p∧q)∨(p∧r) (แจกแจง)

9.) ∼(p∨q) ≡ ∼p∧∼q

10.) ∼(p∧q) ≡ ∼p∨∼q

11.) ∼p→q ≡ p∨∼q **

12.) p→q ≡ ∼p∨q **

13.) p→q ≡ ∼q→∼p

14.) p↔q ≡ (p→q)∧(p→q) ≡ (∼p∨q)∧(∼p∨q)

** เปลี่ยน “ถ้า…แล้ว…” เป็น “หรือ” ง่ายๆ ด้วยประโยค “หน้าเปลี่ยนไป “หรือ” หลังเฉยๆ วิธีนี้ใช้ได้ทั้งไปและกลับ

เช่น

p→q จะเปลี่ยนเป็น “หรือ” : หน้าเปลี่ยนไป คือ ประพจน์ข้างหน้าเปลี่ยนเป็นนิเสธ จะได้ ∼p “หรือ” หลังเฉยๆ คือ ข้างหลังเป็น q เหมือนเดิม ดังนั้น จะได้ ∼p∨q

p∨q จะเปลี่ยนเป็น “ถ้า…แล้ว…” : หน้าเปลี่ยนไป คือ ประพจน์ p เปลี่ยนเป็น นิเสธของ p จะได้ ∼p “แล้ว” หลังเฉยๆ คือ ข้างหลังเป็น q เหมือนเดิม ดังนั้น จะได้ ∼p→q

เราสามารถตรวจสอบว่าประพจน์สมมูลกันหรือไม่ด้วยการสร้างตารางค่าความจริง หรืออาจจะใช้ตัวอย่างการสมมูลข้างต้นมาช่วยตรวจสอบก็ได้(ใช้สูตร)

**การใช้สูตร เราจะทำให้ตัวเชื่อมเหมือนกันและตำแหน่งเดียวกัน เพื่อจะได้สรุปได้ว่าประพจน์ทั้งสองสมมูลกันหรือไม่

เช่น จงพิจารณาว่า ประพจน์ที่ให้มาสมมูลกันหรือไม่ p→∼q กับ q→∼p

วิธีที่ 1 สร้างตารางค่าความจริงได้ ดังนี้

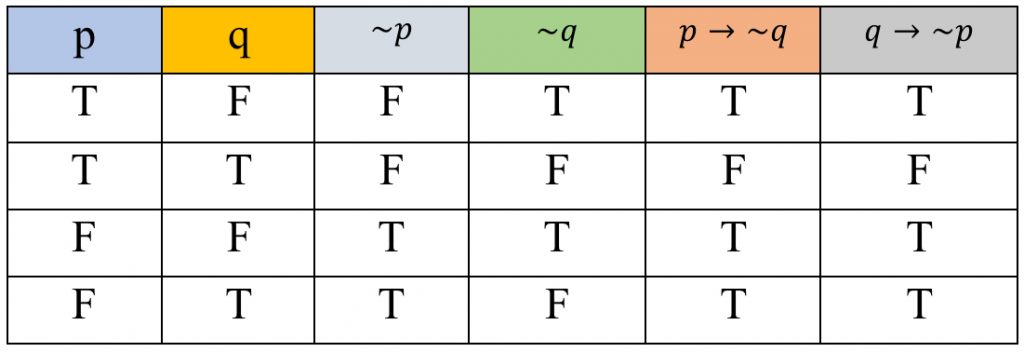
จากตารางค่าความจริง จะเห็นว่า ค่าความจริงของ p→∼q กับ q→∼p มีค่าความจริงเหมือนกันทุกกรณี ดังนั้น p→∼q กับ q→∼p สมมูลกัน

วิธีที่2 ใช้สูตร เราจะสลับ q ให้มาอยู่ข้างหน้า แต่ “→” ไม่สามารถสลับที่ได้ต้องเปลี่ยนให้เป็นตัวเชื่อมที่สลับที่ได้แล้วค่อยเปลี่ยนกลับมาเป็น “→”

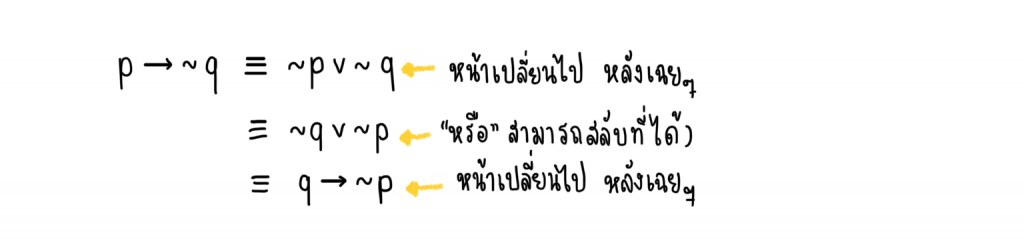
ดังนั้น จะได้ว่า p→∼q กับ q→∼p สมมูลกัน

ลองมาดูอีก 1 ตัวอย่างค่ะ

จงพิจารณาว่า ประพจน์ที่ให้มาสมมูลกันหรือไม่ ∼p∨∼q กับ ∼p→q

วิธีที่ 1 สร้างตารางค่าความจริง

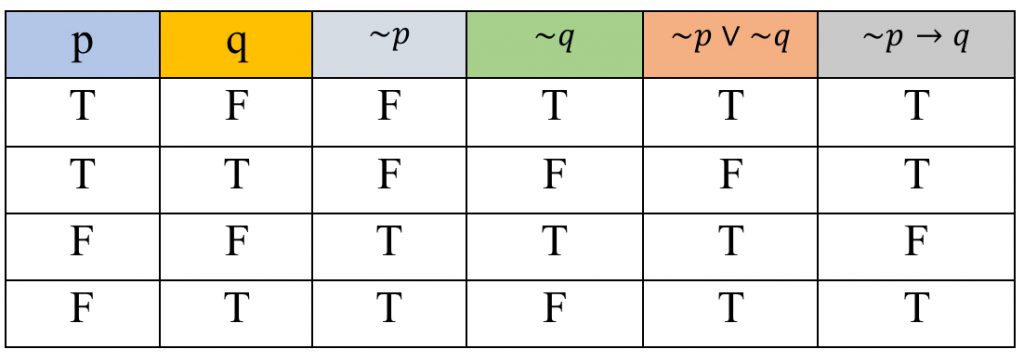
จากตารางจะเห็นว่า ค่าความจริงของ ∼p∨∼q กับ ∼p→q ต่างกันบางกรณี ดังนั้น ∼p∨∼q กับ ∼p→q ไม่สมมูลกัน

วิธีที่ 2 ใช้สูตร เราจะทำให้ ∼p∨∼q อยู่ในรูป “ถ้า…แล้ว…”

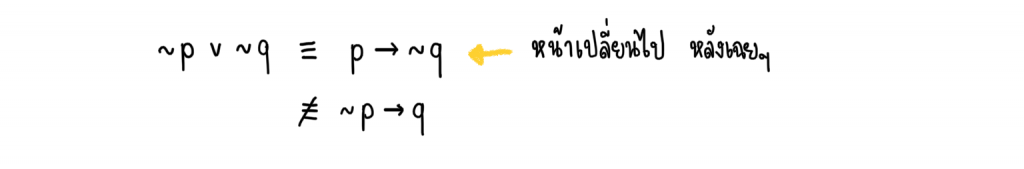
ดังนั้น ∼p∨∼q กับ ∼p→q ไม่สมมูลกัน

น้องๆลองสังเกตดู จะเห็นว่าการใช้ตารางนั้นยุ่งยากและค่อนข้างเสียเวลา

ดังนั้น น้องๆควรหมั่นฝึกฝนทำแบบฝึกหัดการตรวจสอบการสมมูลโดยวิธีใช้สูตร เพื่อจะได้ทำอย่างคล่องแคล่ว แม่นยำ และรวดเร็ว

ตัวอย่าง

เนื่องจากการตรวจสอบโดยใช้ตารางค่าความจริงเป็นวิธีที่ไม่ได้มีอะไรยาก ตัวอย่างต่อไปนี้เราจึงจะใช้วิธีใช้สูตร เพื่อให้น้องๆเข้าใจมากยิ่งขึ้นค่ะ

จงตรวจสอบว่าประพจน์ต่อไปนี้สมมูลกันหรือไม่

1.) ∼(p↔q) กับ ∼p↔∼q

วิธีทำ

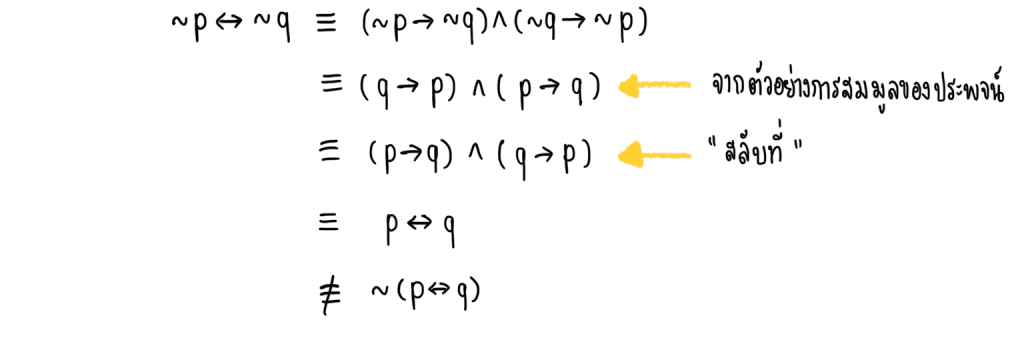
ดังนั้น ∼(p↔q) กับ ∼p↔∼q ไม่สมมูลกัน

2.) p→(q→r) กับ (p∧q)→r

วิธีทำ

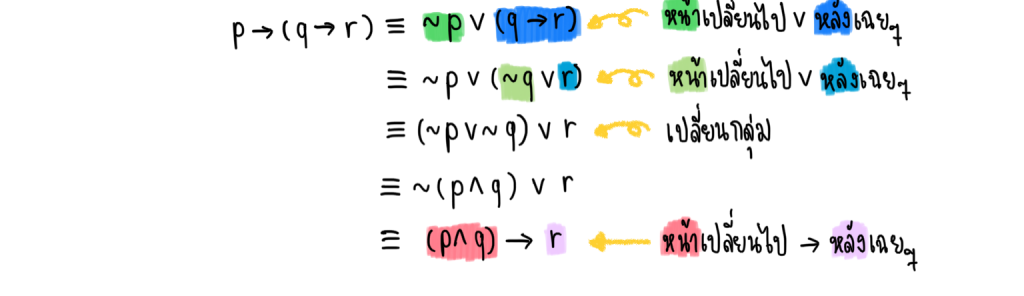
ดังนั้น p→(q→r) กับ (p∧q)→r สมมูลกัน

3.) ∼[(p∧q)→(∼q∨r)] กับ p∧∼(q→r)

วิธีทำ

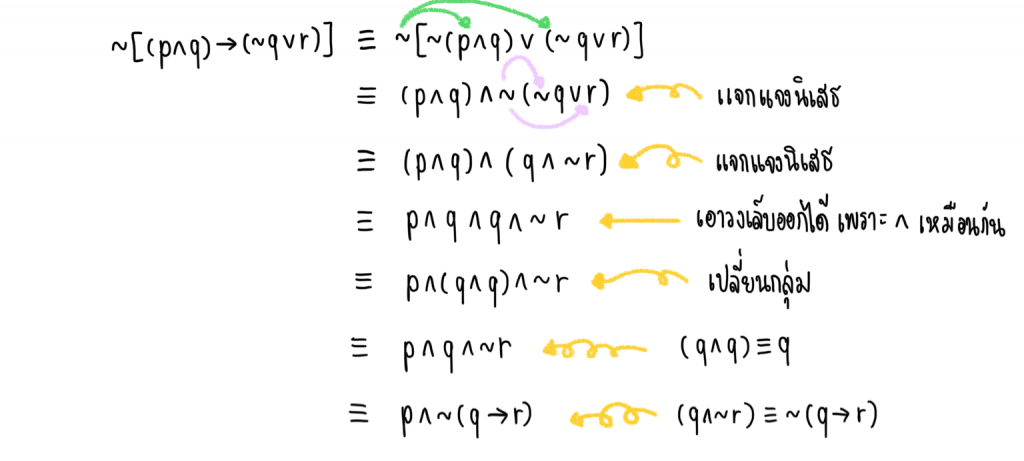
ดังนั้น ∼[(p∧q)→(∼q∨r)] กับ p∧∼(q→r) สมมูลกัน

ไม่มีใครเข้าใจตั้งแต่ครั้งแรกที่เรียน ถ้าน้องเปิดใจให้วิชาคณิตศาสตร์และขยันทำโจทย์ คณิตศาสตร์ก็เป็นอีกหนึ่งวิชาที่สนุก สู้ๆนะคะ❤️❤️