ฟังก์ชันผกผัน
ฟังก์ชันผกผัน หรืออินเวอร์สฟังก์ชัน เขียนแทนด้วย เมื่อ
เป็นฟังก์ชัน
จากที่เรารู้กันว่า ฟังก์ชันนั้นเป็นความสัมพันธ์ ดังนั้นฟังก์ชันก็สามารถหาตัวผกผันได้เช่นกัน แต่ตัวผกผันนั้นไม่จำเป็นที่จะต้องเป็นฟังก์ชันเสมอไป
เพราะอะไรถึงไม่จำเป็นจะต้องเป็นฟังก์ชัน เราลองมาดูตัวอย่างกันค่ะ
ให้ f = {(1, 2), (3, 2), (4, 5),(6, 5)} จะเห็นว่า f เป็นฟังก์ชัน
พิจารณาตัวผกผันของ f เท่ากับ {(2, 1), (2, 3), (5, 4), (5, 6)} จากนิยามของฟังก์ชัน ถ้าตัวหน้าเท่ากันแล้วตัวหลังจะต้องเท่ากัน ทำให้ได้ว่า ตัวผกผันของ f ไม่เป็นฟังก์ชัน
ตัวอย่างตัวผกผันของฟังก์ชัน
หาฟังก์ชันผกผันของ เมื่อ
1.) f(x) =
ให้ f(x) = y
ขั้นตอนที่ 1 เปลี่ยน x เป็น y เปลี่ยน y เป็น x
จะได้
ขั้นที่ 2 จัดรูปให้ y อยู่เดี่ยวๆ
จะได้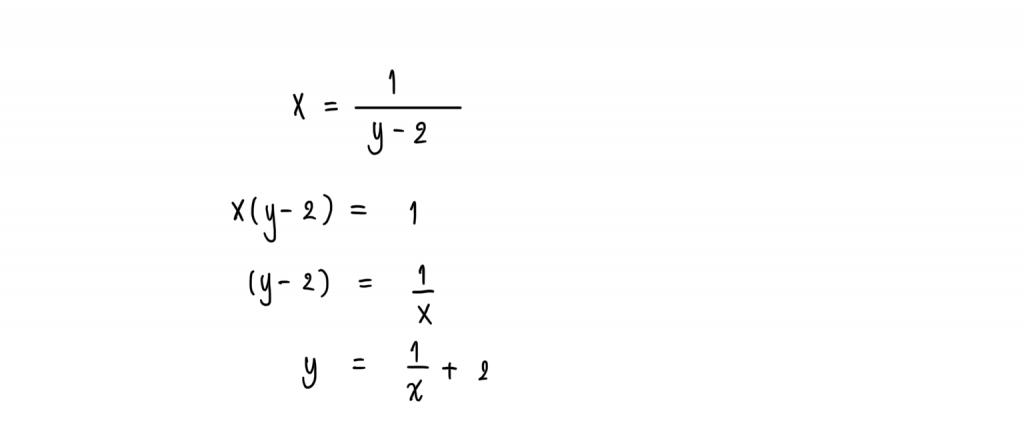 
ดังนั้น = เมื่อ x ≠ 0 (เพราะถ้า x =0จะหาค่าไม่ได้)
2.) f(x) =
ขั้นที่ 1 เปลี่ยน x เป็น y เปลี่ยน y เป็น x
จะได้ x =
ขั้นที่ 2 จัดรูปให้ y อยู่เดี่ยวๆ
จะได้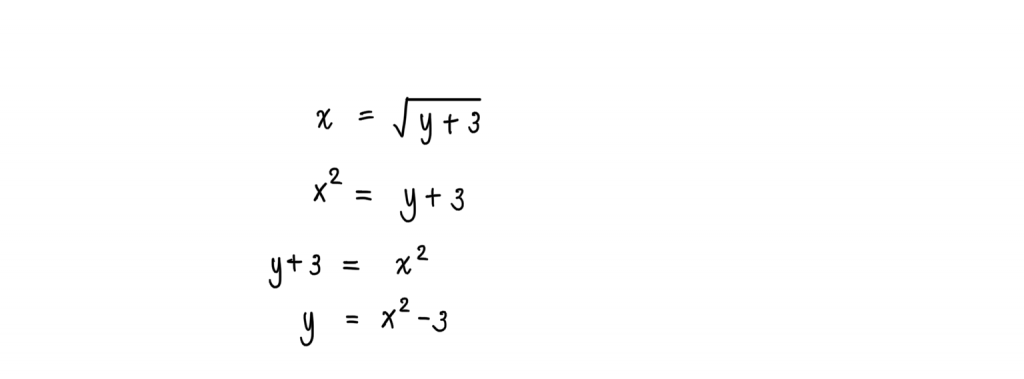 
ดังนั้น =
3.) f(x) =
ขั้นที่ 1 เปลี่ยน x เป็น y เปลี่ยน y เป็น x
จะได้ x =
ขั้นที่ 2 จัดรูปให้ y อยู่เดี่ยวๆ
จะได้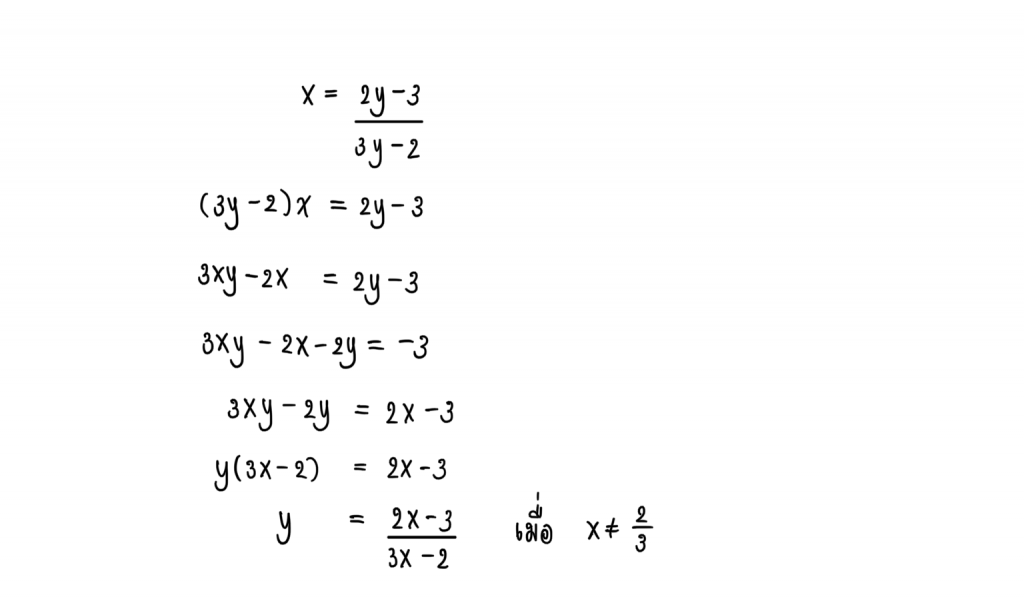 
ดังนั้น =
เมื่อ x ≠
ให้ f(x) = 3x + 5 จงหา
4.)
ขั้นตอนที่ 1 หา
จะได้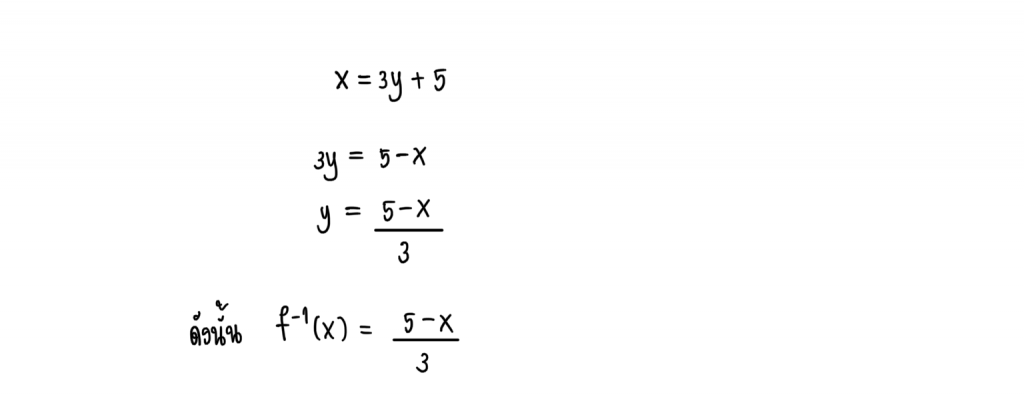 
ขั้นตอนที่ 2 แทนค่า x ด้วย 3
จะได้ =
5.)
ขั้นตอนที่ 1 หา
จะได้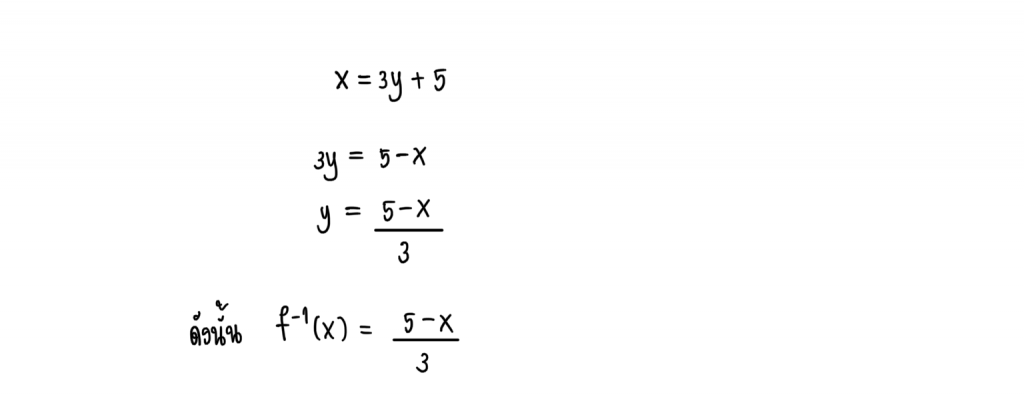
ขั้นตอนที่ 2 แทนค่า x ด้วย -1
จะได้ =
การตรวจสอบว่าตัวผกผันของ f เป็นฟังก์ชันหรือไม่
การตรวจสอบทำได้ 2 วิธี คือ
- หาตัวผกผันมาก่อนแล้วเช็คว่าตัวผกผันนั้นเป็นฟังก์ชันหรือไม่
- หาจากทฤษฎีบทต่อไปนี้
ตัวผกผันของ f เป็นฟังก์ชัน ก็ต่อเมื่อ f เป็นฟังก์ชันหนึ่งต่อหนึ่ง
ขยายความทฤษฎีบท
เรามีข้อความอยู่สองข้อความ ที่มีตัวเชื่อม ก็ต่อเมื่อขั้นกลางอยู่
ถ้าเรารู้ว่าฝั่งใดฝั่งหนึ่งจริง เราสามารถสรุปข้อความอีกฝั่งหนึ่งได้เลย
เช่น ถ้าเรารู้ว่า ตัวผกผันของ f เป็นฟังก์ชัน เราก็จะรู้ด้วยว่า f เป็นฟังก์ชัน
ในขณะเดียวกัน ถ้าเรารู้ว่า f เป็นฟังก์ชันหนึ่งต่อหนึ่ง เราก็จะรู้ว่า ตัวผกผันของ f เป็นฟังก์ชัน
แต่ ถ้าเรารู้ว่าข้อความฝั่งหนึ่งไม่จริง เราก็สามารถสรุปได้เช่นกันว่า ข้อความอีกฝั่งก็ไม่จริง
เช่น เรารู้ว่า ตัวผกผันของ f ไม่เป็นฟังก์ชัน เราสามารถสรุปได้เลยว่า f ไม่เป็นฟังก์ชันหนึ่งต่อหนึ่ง
ถ้าเรารู้ว่า f ไม่เป็นฟังก์ชันหนึ่งต่อหนึ่ง เราสามารถสรุปได้ว่า ตัวผกผันของ f ไม่เป็นฟังก์ชัน
ตัวอย่างการตรวจสอบ ฟังก์ชันผกผัน
ให้ f เป็นฟังก์ชัน ที่ f = {(x, y) : x, y ∈ และ y = 2x + 3}
วิธีทำ 1 จาก f = {(x, y) : x, y ∈ และ y = 2x + 3}
จะได้ว่า = {(y, x ) : y, x ∈
และ y = 2x + 3}
หรือเขียนได้อีกแบบคือ = {(x, y) : x, y ∈
และ x = 2y + 3} << ตรงสมการ เปลี่ยน x เป็น y เปลี่ยน y เป็น x
จะตรวจสอบว่า เป็นฟังก์ชันหรือไม่ โดยสมมติคู่อันดับมาสองคู่ ให้เป็น
ซึ่งทั้งสองคู่อันดับนี้ เป็นคู่อันดับใน
ดังนั้นเราสามารถแทน คู่อันดับทั้งสองไปในสมการ x = 2y + 3 ได้
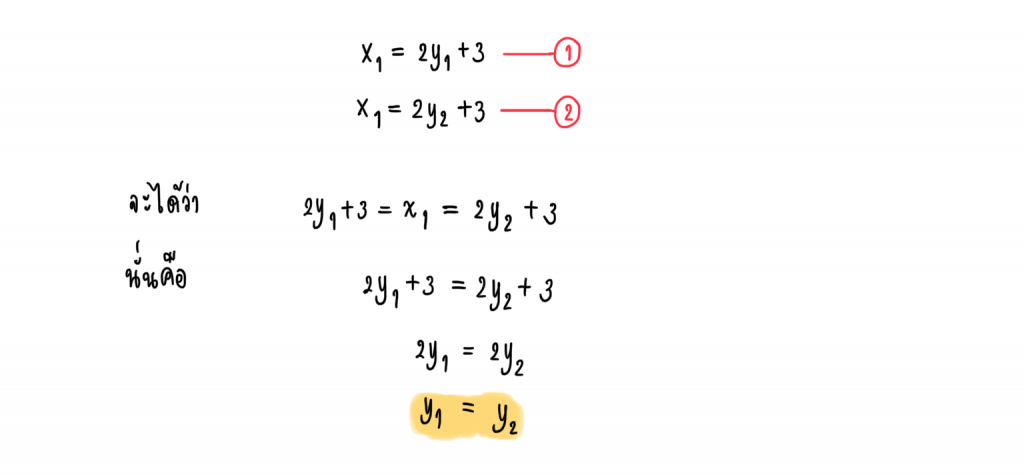
จากนิยามของฟังก์ชันจะได้ว่า เป็นฟังก์ชันเพราะ เมื่อสมาชิกตัวหน้าของคู่อันดับเหมือนกันสมาชิกตัวหลังก็เหมือนกันด้วย
วิธีที่ 2 จาก f = {(x, y) : x, y ∈ และ y = 2x + 3}
จะตรวจสอบว่า f เป็นฟังก์ชันหนึ่งต่อหนึ่งหรือไม่เพื่อนำมาสรุปการเป็นฟังก์ชันของ
สมมติให้ เป็นคู่อันดับใน f
ดังนั้นเราสามารถแทนคู่อันดับทั้งสองคู่อันดับในสมการ y = 2x + 3 ได้
ได้เป็น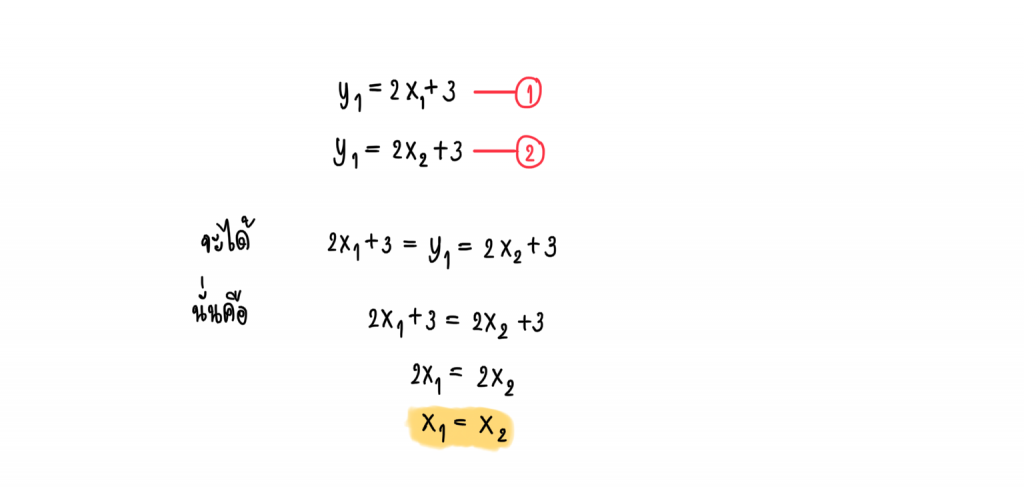 
จากนิยามของฟังก์ชันหนึ่งต่อหนึ่ง จะได้ว่า f เป็นฟังก์ชันหนึ่งต่อหนึ่ง เพราะเมื่อเราให้สมาชิกตัวหลังเท่ากันแล้วเราได้ว่าสมาชิกตัวหน้าก็เท่ากัน
และ จาก f เป็นฟังก์ชันหนึ่งต่อหนึ่งเลยทำให้สรุปได้ว่า เป็นฟังก์ชัน
จากวิธีทั้งสองวิธี น้องๆสามารถเลือกวิธีตรวจสอบที่ตัวเองถนัดได้เลย ได้คำตอบเหมือนกันจ้า
เนื้อหาที่ควรรู้เพื่อง่ายต่อการทำความเข้าใจ
ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง
