เซตคืออะไร?
เซต คือ คำที่ใช้เรียกกลุ่มของสิ่งต่างๆ
ทำไมต้องเรียนเซต
เซตมีประโยชน์ในเรื่องของการจำแนกสิ่งต่างๆออกเป็นกลุ่มๆ อีกทั้งยังแทรกอยู่ในเนื้อหาบทอื่นๆของคณิตศาสตร์ เราจึงจำเป็นต้องทำความเข้าใจเกี่ยวกับเซต เพื่อที่จะเรียนเนื้อหาบทอื่นๆได้ง่ายขึ้น
ความรู้เบื้องต้นเกี่ยวกับเซต
เซต คือคำที่ใช้เรียกกลุ่มของสิ่งต่างๆ เช่น เซตของสระในภาษาอังกฤษ คือ กลุ่มของสระในภาษาอังกฤษ a,e,i,o,u เป็นต้น
สมาชิกของเซต คือ สิ่งที่อยู่ในเซต เช่น เซตของสระในภาษาอังกฤษ สมาชิกของเซต คือ a,e,i,o,u
การเขียนเซต
การเขียนเซตจะเขียนได้ 2 วิธี
1.) เขียนแบบแจกแจงสมาชิก คือการเขียนสมาชิกไว้ในวงเล็บปีกกา “{ }”แล้วคั่นสมาชิกแต่ละตัวด้วย “,” เช่น
ให้ A แทนเซตของจำนวนนับที่น้อยกว่า 10
ดังนั้น A = {1,2,3,4,5,6,7,8,9}
2.) เขียนแบบบอกเงื่อนไข คือการกำหนดตัวแปรขึ้นมาแล้วใส่เงื่อนไขให้ตัวแปรนั้น เช่น
A = {x|x ∈ N และ x < 10} จากข้อความนี้ แปลได้ว่า A เท่ากับ x โดยที่ x เป็นสมาชิกของจำนวนนับและ x น้อยกว่า 10
“|” แทนคำว่า โดยที่ หรืออาจจะใช้ “:” แทนคำว่าโดยที่ก็ได้
ประเภทของเซต
1.) เซตว่าง (Empty set) คือเซตที่มีจำนวนสมาชิกเป็น 0 โดยจะใช้สัญลักษณ์ Ø หรือ { } แทน เซตว่าง
เช่น ให้ A แทนเซตของจำนวนเดือนที่มี 32 วัน เราจะเห็นว่าไม่มีเดือนไหนที่มี 32 วัน ดังนั้น A = Ø หรือ A = { }
2.) เซตจำกัด (Finite set) คือ เซตที่สามารถระบุจำนวนสมาชิกได้
เช่น เซตของของจำนวนนับที่น้อยกว่า 10 สามารถเขียนได้ดังนี้ {1,2,3,4,5,6,7,8,9} จะเห็นว่ามีจำนวนสมาชิกเท่ากับ 9
**เซตว่าง เป็นเซตจำกัด เนื่องจากมีจำนวนสมาชิกเท่ากับ 0**
3.) เซตอนันต์ (infinite set) คือ เซตที่ไม่สามารถระบุจำนวนสมาชิกได้ เช่น
เซตของจำนวนนับ {1,2,3,…} เป็นเซตอนันต์ เพราะเราไม่สามารถบอกได้ว่ามีจำนวนสมาชิกเท่าไหร่
เซตของจำนวนเต็ม {…,-3,-2,-1,0,1,2,3,…} เป็นเซตอนันต์
**{1,2,3,…} หมายถึง มีจำนวนอื่นต่อไปอีกเรื่อยๆ
ตัวอย่าง
1.)
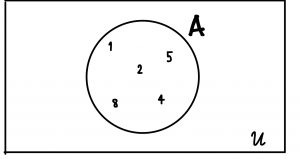
A = {1,2,4,5,8}
จากรูปจะได้ว่า
>> สมาชิกของ A ประกอบด้วย 1,2,4,5,8
>> จำนวนสมาชิกของ A เท่ากับ 5
>> A เป็นเซตจำกัด
2.)
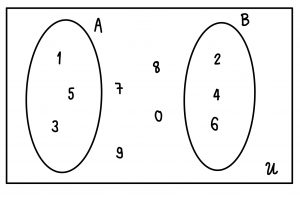
A = {1,3,5} B = {2,4,6}
จากรูป สามารถบอกได้ว่า
>> 1,3,5 เป็นสมาชิกของ A แต่ไม่เป็นสมาชิกของ B
>> 2,4,6 เป็นสมาชิกของ B แต่ไม่เป็นสมาชิกของ A
>> 0,7,8,9 ไม่เป็นสมาชิก ของ A และไม่เป็นสมาชิกของ B
>> A และ B เป็นเซตจำกัด
>> 0,1,2,3,4,5,6,7,8,9 เป็นสมาชิก ของ U
โดยที่ U คือเอกภพสัมพัทธ์
3.)ให้ B เป็นเซตของจำนวนเต็มคู่ที่มากกว่า 0
จะได้ว่า B = {2,4,6,8,…} จะเห็นว่าเราไม่สามารถระบุจำนวนสมาชิกของเซต B ได้ ดังนั้น B เป็นเซตอนันต์