การสร้างตารางค่าความจริงเป็นการทำความเข้าใจว่าประพจน์จะสามารถเป็นจริงหรือเท็จได้กี่กรณี ถ้าเป็นการบรรยายว่าตัวเชื่อมแต่ละตัวเป็นจริงกรณีไหนและเท็จกรณีไหนอาจจะทำให้น้องๆมองภาพไม่ค่อยออก การทำตารางจะทำให้เห็นภาพง่ายขึ้น เราไปดูเนื้อหาการสร้างตารางค่าความจริงกันเลยค่ะ
การสร้างตารางค่าความจริง
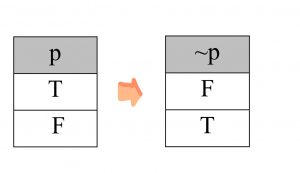
กรณีที่มีประพจน์ 1 ประพจน์ จะมีค่าความจริงที่เป็นไปได้ 2 กรณี ดังนี้
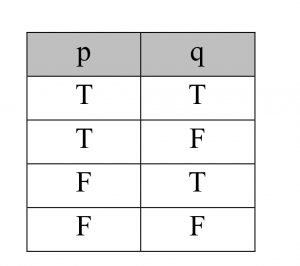
กรณีที่มีประพจน์ 2 ประพจน์ จะมีค่าความจริงที่เป็นไปได้ 4 กรณี ดังนี้
กรณีที่มีประพจน์ 3 ประพจน์ จะมีค่าความจริงที่เป็นไปได้ 8 กรณี ดังนี้
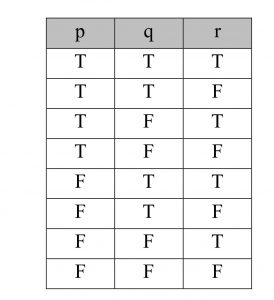
จากทั้ง 3 กรณีแรก เราจะได้ว่า
กรณีที่มีประพจน์ a ประพจน์ จะมีค่าความจริงที่เป็นไปได้ 2ª กรณี
การสร้างตารางค่าความจริงของประพจน์ที่เชื่อมด้วย “หรือ”
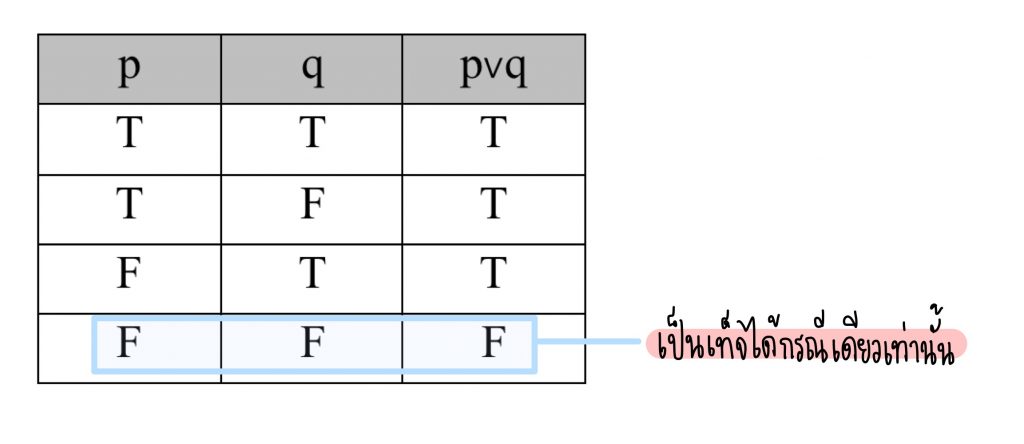
กรณี “หรือ” ถ้ามีตัวใดตัวหนึ่งเป็นจริง ประพจน์ p∨q จะเป็นจริงทันที
เช่น ก. 3+2 = 5 หรือ 3>7
สร้างตารางค่าความจริงได้ดังนี้
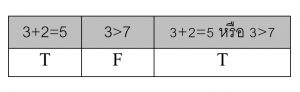
ดังนั้น ประพจน์ 3+2 =5 หรือ 3>7 มีค่าความจริงเป็นจริง (T)
ข. หินเป็นสิ่งมีชีวิต หรือ เชียงใหม่อยู่ภาคใต้ของประเทศไทย
สร้างตารางค่าความจริงได้ ดังนี้

ดังนั้น ประพจน์ หินเป็นสิ่งมีชีวิตหรือเชียงใหม่อยู่ภาคใต้ของประเทศไทย มีค่าความจริงเป็นเท็จ(F)
การสร้างตารางค่าความจริงของประพจน์ที่เชื่อมด้วย “และ”
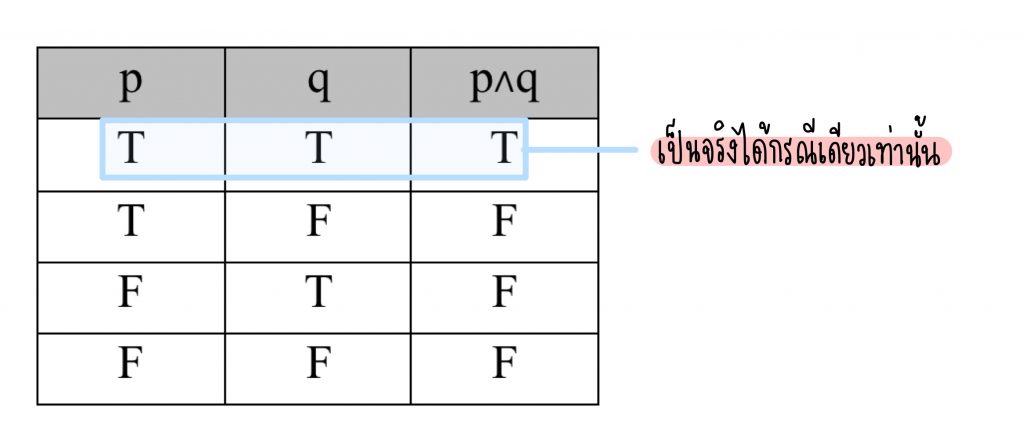
เช่น ก. จำนวนนับมีค่ามากกว่า 0 และ 1>0
สร้างตารางค่าความจริงได้ ดังนี้

ดังนั้น ประพจน์จำนวนนับมีค่ามากกว่า0 และ 1>0 มีค่าความจริงเป็นจริง
ข.) 2 หาร 20 ลงตัว และ 2 เป็นจำนวนคี่
สร้างตารางค่าความจริงได้ ดังนี้
ดังนั้น ประพจน์ 2 หาร 20ลงตัว และ 2 เป็นจำนวนคี่ มีค่าความจริงเป็นเท็จ
การสร้างตารางค่าความจริงของประพจน์ที่เชื่อมด้วย “ถ้า…แล้ว…”
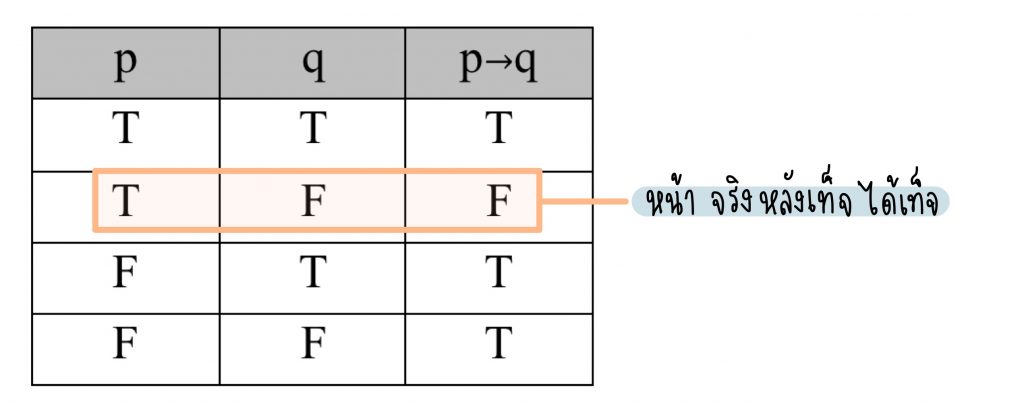
เช่น ก. ถ้า 2 เป็นจำนวนคี่ แล้ว ½ = 0.5
สามารถสร้างตารางค่าความจริงได้ ดังนี้

ดังนั้น ประพจน์ ถ้า 2 เป็นจำนวนคี่ แล้ว ½ = 0.5 มีค่าความจริงเป็นจริง
ข. 1<2 แล้ว -1>2
สามารถสร้างตารางค่าความจริงได้ ดังนี้

ดังนั้น ประพจน์ 1<2 แล้ว -1>2 มีค่าความจริงเป็นเท็จ
การสร้างตารางค่าความจริงของประพจน์ที่เชื่อมด้วย “ก็ต่อเมื่อ”
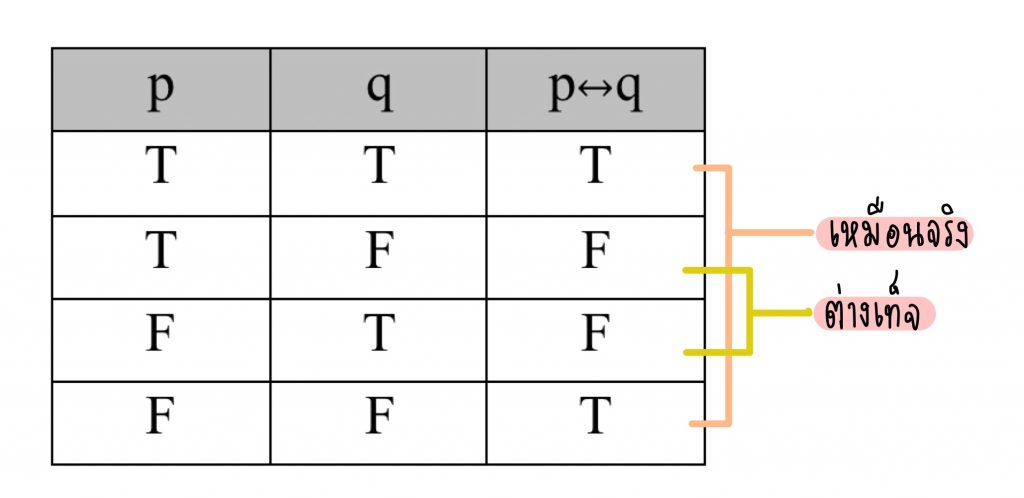
ตัวอย่างการสร้างตารางค่าความจริง
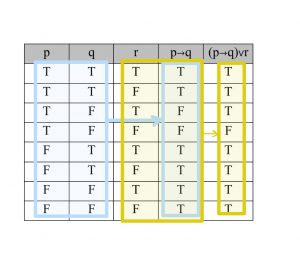
1.) สร้างตารางค่าความจริงของประพจน์ (p→q)∨r
วิธีทำ
- ทำในวงเล็บก่อน จะได้ค่าความจริง p→q ตามตาราง
- จากนั้นนำค่าความจริงที่ได้ใน ช่อง p→q ไปเชื่อมกับ r จะได้ค่าความจริงตามตารางช่อง (p→q)∨r
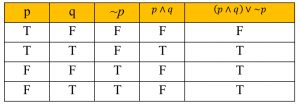
2.) สร้างตารางค่าความจริงของประพจน์ (p∧q)∨∼p
วิธีทำ
- ทำจากข้างในวงเล็บ คือพิจารณา (p∧q)
- พอได้ค่าความจริงมาแล้วก็มาพิจารณา (p∧q)∨∼p ได้ค่าความจริงดังตาราง
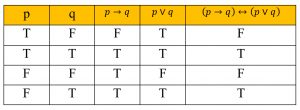
3.) จงสร้างตารางค่าความจริงของประพจน์ (p→q)↔(p∨q)
วิธีทำ
- อาจจะเริ่มพิจารณาจาก (p→q) แล้วไปพิจารณา (p∨q)
- พอได้ค่าความจริงของทั้งสองประพจน์แล้ว เราจะพิจารณา (p→q)↔(p∨q) แล้วจะได้ตารางค่าความจริง ดังตาราง