การดำเนินการของฟังก์ชัน

การดำเนินการของฟังก์ชัน ประกอบไปด้วย การบวก การลบ การคูณ และการหารของฟังก์ชัน ซึ่งเมื่อเราดำเนินการที่กล่าวมาข้างต้นกับฟังก์ชันแล้วจะทำให้เกิดฟังก์ชันใหม่ขึ้นมา เขียนแทนด้วย f + g, f – g, fg ,   ตามลำดับ โดยที่

(f + g)(x) = f(x) + g(x)

(f – g)(x) = f(x) – g(x)

(fg)(x)    = f(x)g(x)

โดเมนของ f + g, f – g, fg คือ โดยที่ ≠

(x)  =   โดยที่ g(x) ≠ 0 และ โดเมน คือ ลบเซตของ x โดยที่ x อยู่ในโดเมนของ g ที่ทำให้ g(x) = 0

 

เช่น

กำหนดให้ f(x) = 2x + 3  และ g(x) = x² – 9

จะเห็นว่า และ

(f + g)(x) = f(x) + g(x) = (2x + 3) + (x² – 9) = x² + 2x -6

(f – g)(x) = f(x) – g(x) = (2x + 3) – (x² – 9) = -x² + 2x + 12

(fg)(x)    = f(x)g(x) = (2x + 3)(x² – 9) = 2x³ + 3x² – 18x -27

(x)  =   = โดยที่ x ≠ ±3

 

ตัวอย่างโจทย์ปัญหาการดำเนินการของฟังก์ชัน

 

1.) ให้ f(x) = x² + 2 และ g(x) = 2x จงหา (f + g)(1) และ (f – g)(4)

วิธีทำ 

จากโจทย์ จะได้ว่า  และ   ดังนั้นจะได้ว่า =

พิจารณา (f + g)(x) = f(x) + g(x) = x² + 2 + 2x

แทนค่า x = 1 จะได้ว่า (f + g)(1) = (1)² + 2 + 2(1) = 5

พิจารณา (f – g)(x) = f(x) – g(x) = x² + 2 – 2x

แทนค่า x = 4 จะได้ว่า (f – g)(4) = (4)² + 2 – 2(4) = 16 +2 – 8 = 10

ดังนั้น  (f + g)(1) = 5 และ (f – g)(4) = 10

 

2.) f(x) =   และ g(x) =   หา (fg)(2), (fg)(4) และ (fg)(6)

วิธีทำ หาโดเมนของ (fg)(x) จะได้

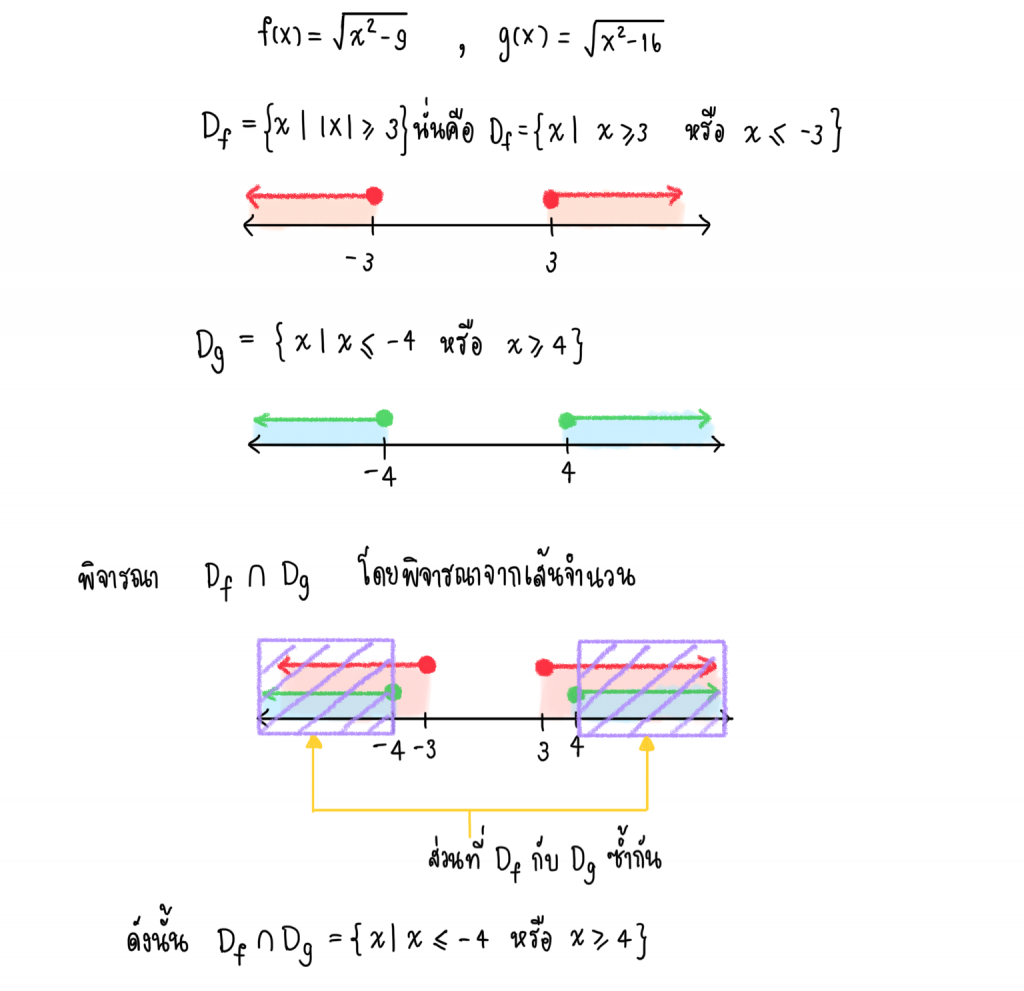
พิจารณา (fg)(x) = f(x)g(x) = ()()

พิจารณาที่ x = 2 จะได้ว่า (fg)(2) หาค่าไม่ได้ เนื่องจาก 2 ∉

ที่ x = 4 จะได้ว่า (fg)(4) =

ที่ x = 6 จะได้ว่า (fg)(6) =