ตัวคูณร่วมน้อย (ค.ร.น.)
น้องๆ ทราบหรือไม่ว่า การหาตัวคูณร่วมน้อย (ค.ร.น.) ของจำนวนนับตั้งแต่สองจำนวนขึ้นไปนั้น เป็นการหาตัวตั้งร่วมหรือพหุคูณร่วมที่มีค่าน้อยที่สุดของจำนวนนับเหล่านั้น บทความนี้ได้รวบรวม ตัวอย่าง ค.ร.น. พร้อมทั้งแสดงวิธีทำอย่างละเอียด โดยมีวิธี การหา ค.ร.น. ทั้งหมด 3 วิธี ดังนี้
- การหา ค.ร.น. โดยการหาผลคูณร่วม
- การหา ค.ร.น. โดยการแยกตัวประกอบ
- การหา ค.ร.น. โดยการหาร (หารสั้น)
ก่อนอื่นที่จะไปเรียนรู้วิธี การหา ค.ร.น. ทั้ง 3 แบบนั้น น้องๆมาทำความรู้จักกับตัวคูณร่วมน้อย(ค.ร.น.) กันก่อนนะคะ
ตัวคูณร่วมน้อย(ค.ร.น.) ของจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป หมายถึง ตัวตั้งร่วมหรือพหุคูณร่วมที่มีค่าน้อยที่สุดของจำนวนนับเหล่านั้น
ก่อนที่จะไปเรียนรู้วิธี การหา ค.ร.น. วิธีแรกนั้น น้องๆจำเป็นต้องศึกษาและแยกแยะความแตกต่างระหว่างการหาตัวประกอบและพหุคูณของจำนวนนับใดๆ
น้องๆ ลองท่องสูตรคูณแม่ 2 หน่อยค่ะ จะได้ ตัวเลขที่เรียงกันในรูปแบบด้านล่าง
2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 , 22 , 24 , …
สังเกตได้ว่าจำนวนซึ่งเป็นสูตรคูณของแม่ 2 แต่ละจำนวนนั้น คือ พหุคูณของ 2 และเขียนว่า “ พหุคูณของ 2 ” ดังนี้
2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 , 22 , 24 , … เป็นพหุคูณของ 2
สังเกตพหุคูณของ 2 ว่าจำนวนใดที่สามารถหารทุกจำนวนได้ลงตัว จะได้ว่า 2 เป็นจำนวนที่หารพหุคูณของ 2 ได้ลงตัวทุกจำนวน สรุปได้ว่า พหูคูณของ 2 คือ จำนวนที่มี 2 เป็นตัวประกอบ
ในทำนองเดียวกัน ถ้าท่องสูตรคูณแม่ 3 และ 4 สังเกตว่ามีลักษณะเดียวกันกับสูตรคูณของแม่ 2
3 , 6 , 9 , 12 , 15 , 18 , 21 , 24 , 27 , 30 , 33 , 36 … เป็นพหุคูณของ 3
4 , 8 , 12 , 16 , 20 , 24 , 28 , 32 , 36 , 40 , 44 , 48 … เป็นพหุคูณของ 4
เมื่อน้องๆรู้จักพหุคูณของจำนวนแต่ละจำนวนแล้ว ต่อไปมาทำความรู้จักพหุคูณร่วม และตัวประกอบของจำนวนนับใดๆ โดยศึกษาจากโจทย์ต่อไปนี้
- ตัวประกอบของ 3 คือ 1 และ 3 พหุคูณของ 3 คือ 3, 6, 9, 12, …
- ตัวประกอบของ 4 คือ 1, 2 และ 4 พหุคูณของ 4 คือ 4, 8, 16, 20, …
- ตัวประกอบของ 5 คือ 1 และ 5 พหุคูณของ 5 คือ 5, 10, 15, 20, …
เมื่อศึกษาครบทั้ง 3 ข้อแล้ว สามารถสรุปความหมายของ ตัวตั้งร่วมหรือพหุคูณร่วมของจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป ซึ่งหมายถึง จำนวนนับใด ๆ ที่หารด้วยจำนวนนับนั้นลงตัวทุกจำนวน
พหุคูณร่วมของจำนวนนับที่มีค่าน้อยที่สุด เรียกว่า ตัวคูณร่วมที่น้อยที่สุด หรือ ค.ร.น. ต่อไปมาดูนิยามเกี่ยวกับ ค.ร.น. กันนะคะ
ลำดับถัดไปจะนำน้องๆ ไปศึกษาวิธี การหา ค.ร.น. ทั้ง 3 วิธี ถ้าพร้อมแล้วมาเริ่มวิธีแรกกันเลยนะคะ
วิธีที่ 1 การหา ค.ร.น. โดยการหาผลคูณร่วม
หลักการ
- หาตัวตั้งหรือพหุคูณของจำนวนนับที่ต้องการหา ค.ร.น.
- พิจารณาตัวตั้งร่วมหรือพหุคูณร่วมที่มีค่าน้อยที่สุด
- ค.ร.น. คือ ตัวตั้งร่วมหรือพหุคูณร่วมที่มีค่าน้อยที่สุด
เมื่อศึกษาหลักการหา ค.ร.น. โดยการหาผลคูณร่วม เรียบร้อยแล้ว น้องๆมาศึกษาตัวอย่างได้เลยคะ
ตัวอย่างที่ 1 จงหา ค.ร.น. ของ 2 และ 3
วิธีทำ พหุคูณของ 2 คือ 2, 4, 6, 8, 10, 12, 14, 16, 18, …
พหุคูณของ 3 คือ 3, 6, 9, 12, 15, 18, 21, 24, …
เรียก 6, 12, 18, … เป็นพหุคูณร่วมของ 2 และ 3
พหุคูณที่น้อยที่สุดของ 2 และ 3 เรียกว่า ตัวคูณร่วมที่น้อยที่สุด ซึ่งเขียนย่อๆ ว่า ค.ร.น.
ดังนั้น ค.ร.น. ของ 2 และ 3 คือ 6
ตัวอย่างที่ 2 จงหา ค.ร.น. ของ 2, 3 และ 4
วิธีทำ พหุคูณของ 2 คือ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, …
พหุคูณของ 3 คือ 3, 6, 9, 12, 15, 18, 21, 24, 27, …
พหุคูณของ 4 คือ 4, 8, 12, 16, 20, 24, 28, …
เพราะฉะนั้น พหุคูณร่วมของ 2, 3 และ 4 คือ 12 และ 24
นั่นคือ 12 เป็นพหุคูณร่วมที่น้อยที่สุดของ 2, 3 และ 4
ดังนั้น ค.ร.น. ของ 2, 3 และ 4 คือ 12
การหา ค.ร.น. โดยใช้วิธีที่ 1 ง่ายมากเลยใช่มั้ยค่ะ ต่อไปน้องๆ มาศึกษาวิธี การหา ค.ร.น. โดยการแยกตัวประกอบ ได้เลยคะ
วิธีที่ 2 การหา ค.ร.น. โดยการแยกตัวประกอบ
หลักการ
- แยกตัวประกอบทั้งหมดของจำนวนนับที่ต้องการหา ค.ร.น.
- พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมของจำนวนนับที่จะหา ค.ร.น.
- พิจารณาตัวประกอบเฉพาะเดี่ยว ๆ
- นำตัวประกอบเฉพาะที่ได้จากข้อ 2. ทั้งหมด และข้อ 3. ทั้งหมด มาคูณกัน
- ค.ร.น. คือ ผลคูณในข้อ 4.
ตัวอย่างที่ 3 จงหา ค.ร.น. ของ 24 และ 32
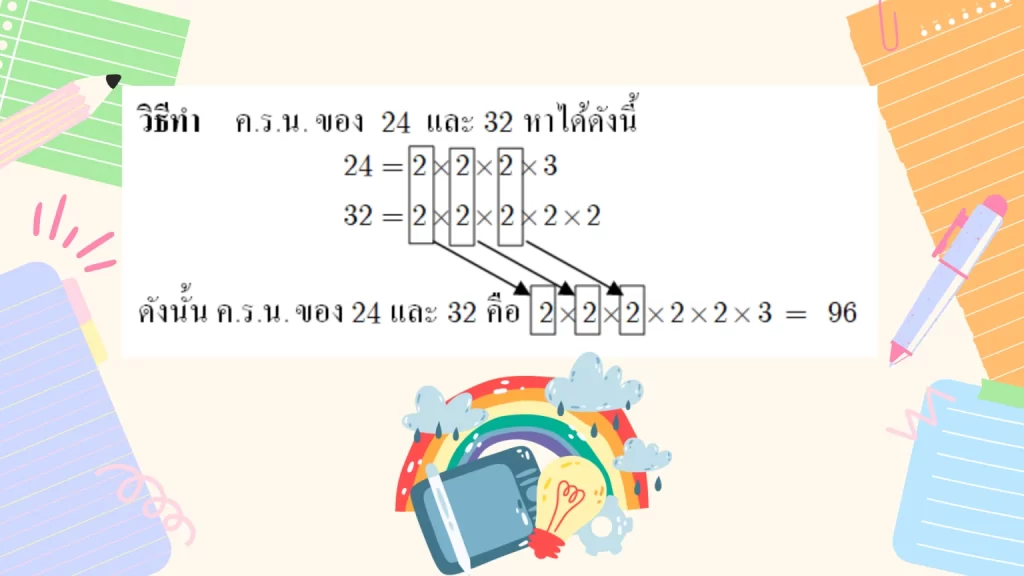
ตัวอย่างที่ 4 จงหา ค.ร.น. ของ 6, 10 และ 12
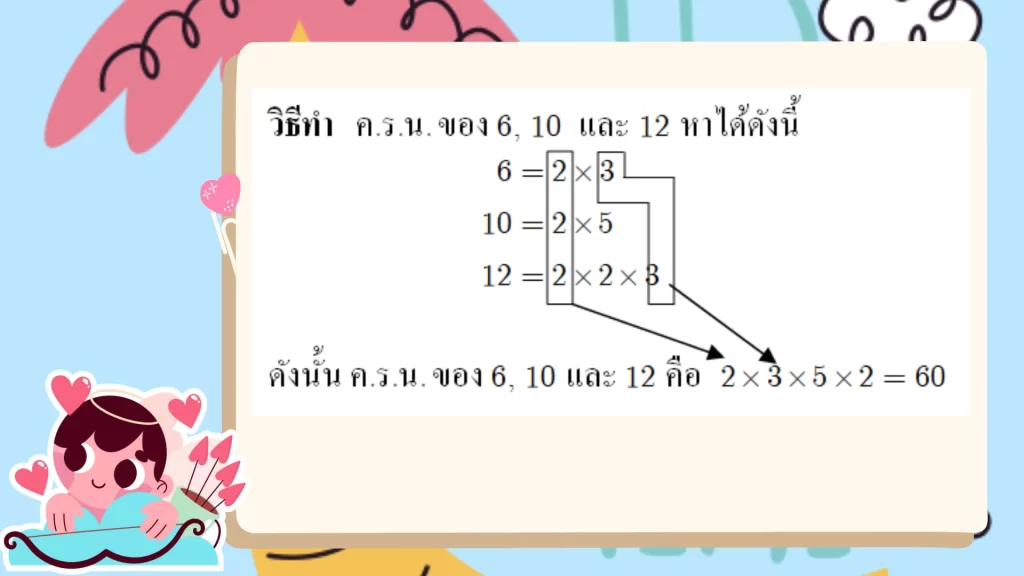
หมายเหตุ : จำนวนนับที่นำมาหา ค.ร.น. ถ้ามี 3 จำนวน ให้นำตัวซ้ำกัน 3 ตัวมา 1 ตัว และซ้ำกัน 2 ตัวมา 1 ตัว มาคูณกัน และคูณกับตัวที่เหลือที่ไม่ได้ซ้ำ ดังตัวอย่างข้างต้น
จะดีกว่ามั้ยคะ ถ้ามีวิธีการที่จะสามารถหา ค.ร.น. ได้รวดเร็วยิ่งขึ้น แต่ทั้งนี้ทั้งนั้นขึ้นอยู่กับความถนัดของแต่ละบุคคลนะคะ น้องๆ ลองศึกษาวิธีสุดท้ายได้โดยใช้วิธีที่ 1 ง่ายมากเลยใช่มั้ยค่ะ ต่อไปน้องๆ มาศึกษาวิธี การหา ค.ร.น. โดยการแยกตัวประกอบ ได้เลยคะ
วิธีที่ 3 การหา ค.ร.น. โดยการหาร (หารสั้น)
หลักการ
- ในแต่ละขั้นตอนของการหาร จะต้องเลือกตัวหาร โดยเลือกจากจำนวนเฉพาะที่เป็นตัวประกอบร่วมอย่างน้อยสองจำนวน ซึ่งอาจมีหลายจำนวน ให้เลือกจำนวนใดไปหารก่อนก็ได้
- นำตัวหารที่ได้จากข้อ 1. มาหาร
- หารต่อไปเรื่อย ๆ จนกระทั่งไม่มีจำนวนเฉพาะที่เป็นตัวประกอบร่วมของสองจำนวนใด ๆ
- ค.ร.น. คือ ผลคูณของจำนวนเฉพาะที่นำไปหารในแต่ละขั้นตอน และจำนวนที่เหลือจากการหารทั้งหมด
ตัวอย่างที่ 5 จงหา ค.ร.น. ของ 18, 24 และ 48
วิธีทำ 2) 18 24 48
3) 9 12 24
2) 3 4 8
2) 3 2 4
3 1 2
ดังนั้น ค.ร.น. ของ 18, 24 และ 48 คือ 2 x 3 x 2 x 2 x 3 x 1 x 2 = 144
ตัวอย่างที่ 6 จงหา ค.ร.น. ของ 30, 18 และ 20
วิธีทำ 2 )30 18 20
5 )15 9 10
3 ) 3 9 2
1 3 2
ดังนั้น ค.ร.น. ของ 30, 18 และ 20 คือ 2 x 5 x 3 x 1 x 3 x 2 = 180
ตัวอย่างที่ 7 จงหา ค.ร.น. ของ 40, 48 และ 18
วิธีทำ 2 )40 48 18
2 )20 24 9
3 )10 12 9
2 )10 4 3
5 2 3
ดังนั้น ค.ร.น. ของ 40, 48 และ 18 คือ 2 x 2 x 3 x 2 x 5 x 2 x 3 = 720
ตัวอย่างเพิ่มเติม
ตัวอย่างที่ 8 จงหา ค.ร.น. ของ 13 และ 29
วิธีทำ เนื่องจาก 13 เป็นจำนวนเฉพาะ และ 13 หาร 29 ไม่ลงตัว
จะได้ว่า พหุคูณร่วมที่น้อยที่สุดของ 13 หาร 29 คือ 13 x 29 = 377
ดังนั้น ค.ร.น. ของ 13 และ 29 คือ 377
ตัวอย่างที่ 9 จงหา ค.ร.น. ของ 53 และ 69
วิธีทำ เนื่องจาก 53 เป็นจำนวนเฉพาะ และ 53 หาร 69 ไม่ลงตัว
จะได้ว่า พหุคูณร่วมที่น้อยที่สุดของ 53 หาร 69 คือ 53 x 69 = 3,657
ดังนั้น ค.ร.น. ของ 53 และ 69 คือ 3,657
เมื่อน้องๆเรียนรู้เรื่อง ตัวคูณร่วมน้อย (ค.ร.น.) จาก ตัวอย่าง ค.ร.น. หลายๆตัวอย่าง จะเห็นได้ชัดว่า การหา ค.ร.น. ไม่ได้เป็นเรื่องยากอย่างที่คิด ลำดับต่อไปที่น้องๆต้องเรียนรู้คือ โจทย์ปัญหาเกี่ยวกับ ห.ร.ม. และ ค.ร.น. ซึ่งจะเป็นการฝึกน้องๆได้การวิเคราะห์โจทย์และเลือกใช้วิธีการแก้ปัญหาของโจทย์แต่ละข้อได้อย่างรวดเร็วและแม่นยำ
คลิปวิดีโอ การหา ค.ร.น.
คลิปวิดีโอนี้ได้รวบรวมวิธีการหา ตัวคูณร่วมน้อย (ค.ร.น.) ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค การหา ค.ร.น. รวมถึงการอธิบาย ตัวอย่าง ค.ร.น. และสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย

















