ความยาวรอบรูปเเละพื้นที่ของวงกลม

phanuphong

คณิตศาสตร์ ป.6, ความยาวรอบรูปวงกลม, พื้นที่วงกลม, วงกลม

Add LINE friends for one click to find article.

ความยาวรอบรูปเเละพื้นที่ของวงกลม

ความยาวรอบรูปของวงกลม หรือเรียกว่า ความยาวเส้นรอบวงของวงกลม คือ ความยาวของเส้นรอบวงกลมสามารถคำนวณได้ ดังนี้

$C = 2\pi r$

โดย: C คือ ความยาวของเส้นรอบวง (หน่วยเป็น เมตร, เซนติเมตร, มิลิเมตร เป็นต้น)

π คือ อัตราส่วนระหว่างเส้นรอบวงกับรัศมี มีค่าประมาณ 22/7 หรือ 3.14

r คือ รัศมีของวงกลม (หน่วยเป็น เมตร, เซนติเมตร, มิลิเมตร เป็นต้น)

พื้นที่ของวงกลม คือ พื้นที่ทั้งหมดที่อยู่ภายในขอบเขตของเส้นรอบวง ซึ่งสามารถคำนวณได้ดังนี้

$A = \pi r^{2}$

โดย: A คือ พื้นที่ของวงกลม (หน่วยเป็น เมตร, เซนติเมตร, มิลิเมตร เป็นต้น)

π คือ อัตราส่วนระหว่างเส้นรอบวงกับรัศมี มีค่าประมาณ 22/7 หรือ 3.14

r คือ รัศมีของวงกลม (หน่วยเป็น เมตร, เซนติเมตร, มิลิเมตร เป็นต้น)

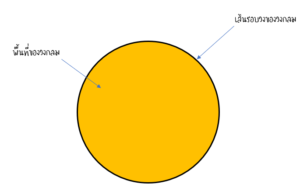
ตัวอย่างโจทย์ความยาวรอบรูปเเละพื้นที่ของวงกลม

ตัวอย่างที่ 1 จงหาความยาวของเส้นรอบวงของวงกลมต่อไปนี้ (กำหนดให้ π = 22/7)

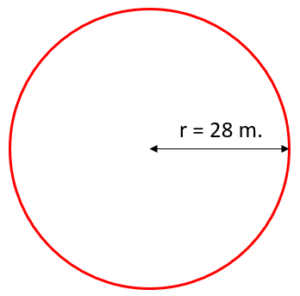
วิธีทำ
2πr = 2 x (22/7) x 28 (ตัด 28 กับ 7)
= 2 x 22 x 4
= 176 เมตร

ตอบ เส้นรอบวงยาว 176 เมตร

ตัวอย่างที่ 2 จงหาความยาวรอบสนามเด็กเล่นของโรงเรียนเเมวน้ำวิทยา เเละพื้นที่ของสนามเด็กเล่น (กำหนดให้ π = 3.14 )

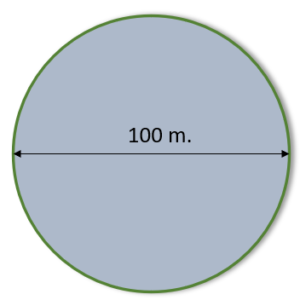วิธีทำ จากรูปจะสังเกตได้ว่าโจทย์ให้เส้นผ่านศูนย์กลางมา ซึ่งรัศมีจะมีขนาดเป็นครึ่งหนึ่งของเส้นผ่านศูนย์กลาง
ดังนั้น รัศมี = 50 เมตร
ความยาวรอบวงของวงกลมมีค่า
2πr = 2 x 3.14 x 50
= 314 เมตร

พื้นที่ของวงกลม = $\pi r^{2}$

= 3.14 x 50 x 50

= 7850 ตารางเมตร

ตอบ ความยาวรอบสนามเด็กเล่นมีค่า 314 m. เเละมีพื้นที่ 7850 ตารางเมตร

ตัวอย่างที่ 3 วงกลมวงหนึ่งมีเส้นรอบวงยาว 94.2 มิลลิเมตร วงกลมนี้จะมีรัศมียาวเท่าใด เเละมีพื้นที่เท่าใด (กำหนดให้ π = 3.14)

ความยาวเส้นรอบวง = 2πr

94.2 = 2 x 3.14 x r

94.2 = 6.28 x r

ย้ายข้าง 6.28 ไปหา 94.2 เพื่อหาค่า r

94.2/6.28 = r

ดังนั้น r = 15 มิลลิเมตร

พื้นที่ของวงกลม = $\pi r^{2}$

= 3.14 x 15 x 15

= 706.5 ตารางมิลลิเมตร

ตอบ รัศมีของวงกลมยาว 15 มิลลิเมตร เเละมีพื้นที่ 706.5 ตารางมิลลิเมตร

ตัวอย่างที่ 4 จงหาความยาวของเส้นรอบวงเเละพื้นที่ของวงกลมที่อยู่เเนบชิดในสี่เหลี่ยมจตุรัสที่มีพื้นที่ภายในสี่เหลี่ยมจตุรัสเท่ากับ 100 ตารางเซนติเมตร (กำหนดให้ π = 3.14)

วิธีทำ สร้างรูปวงกลมที่อยู่ในสี่เหลี่ยมขึ้นมาได้ดังนี้

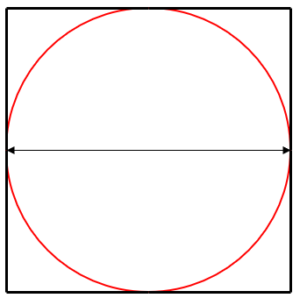
จากภาพที่สร้างขึ้นจะเห็นได้ว่าความยาวเส้นผ่านศูนย์กลางของวงกลมมีขนาดเท่ากับความยาวด้านของสี่เหลี่ยมจตุรัส

ดังนั้น พื้นที่ของสี่เหลี่ยมจตุรัส = ความยาวด้าน x ความยาวด้าน

100 ตร.ซม. = d x d (กำหนดให้ d = ความยาวด้านของสี่เหลี่ยม)
100 ตร.ซม. = $d^{2}$

จะเห็นได้ว่าพื้นที่ของสี่เหลี่ยมจตุรัสมีค่าเท่ากับ 100 ตร.ซม. ซึ่ง 100 เท่ากับ 10 x 10
ดังนั้น ความยาวด้านของสี่เหลี่ยมจตุรัส = 10 เซนติเมตร
เเสดงว่าความยาวเส้นผ่านศูนย์กลางของวงกลม = 10 เซนติเมตร
เเละรัศมีของวงกลม = 5 เซนติเมตร

ความยาวเส้นรอบวงของวงกลม = 2πr

= 2 x 3.14 x 5

= 31.4 เซนติเมตร

พื้นที่ของวงกลม = $\pi r^{2}$

= 3.14 x 5 x 5

= 78.5 ตารางเซนติเมตร

ตอบ ความยาวเส้นรอบวงของวงกลมมีค่า 31.4 เซนติเมตร เเละพื้นที่ 78.5 ตารางเซนติเมตร

หากน้อง ๆ สามารถคำนวณความยาวรอบรูปเเละพื้นที่ของวงกลมได้เเล้ว น้อง ๆ สามารถนำไปประยุกต์ใช้ในชีวิตประจำวันได้หลากหลายในอนาคต น้องสามารถศึกษาการหา ความยาวรอบรูปเเละพื้นที่วงกลม เพิ่มเติมได้ในคลิปวิดีโอด้านล่าง

คลิปวิดีโอ ความยาวรอบรูปเเละพื้นที่วงกลม

คลิปวิดีโอนี้ได้รวบรวมวิธีหา ความยาวรอบรูปเเละพื้นที่วงกลม ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยความรู้ เเละเทคนิครวมถึงการอธิบาย ตัวอย่าง เเละสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

โดเมนของความสัมพันธ์

โดเมนของความสัมพันธ์ โดเมนของความสัมพันธ์ r คือ สมาชิกตัวหน้าของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหน้า เช่น = {(2, 2), (3, 4), (8, 9)} จะได้ว่า = {2, 3, 8}

กลอนสุภาพ แต่งอย่างไรให้ไพเราะ

กลอนสุภาพ เป็นคำประพันธ์ที่หลาย ๆ คนคงจะรู้จักกันดีเพราะพบเจอในวรรณคดีได้ง่าย ใช้กันอย่างแผ่หลาย บทเรียนในวันนี้จะพาน้อง ๆ ทุกคนมาสวมบทนักกวี ฝึกแต่งกลอนสุภาพกันอย่างง่าย ๆ จะมีวิธีและรูปฉันทลักษณ์อย่างไร ไปดูกันเลยค่ะ ความรู้ทั่วไปเที่ยวกับกลอนสุภาพ กลอนสุภาพ หมายถึง กลอนเพลงยาว บางครั้งเรียก กลอนแปด กลอนตลาด กลอนสุภาพ เป็นกลอนประเภทหนึ่งที่เรียบเรียงเข้าเป็นคณะ ใช้ถ้อยคำและทำนองเรียบ ๆ

อิเหนา ตอน ศึกกะหมังกุหนิง เรียนรู้ตัวบทและคุณค่าในเรื่อง

จากที่ได้เรียนรู้ประวัติความเป็นมาและเรื่องย่อของอิเหนากันไปแล้ว บทเรียนภาษาไทยในวันนี้เราจะยังอยู่กับอิเหนากันนะคะ เพราะนอกจากที่มาและเรื่องย่อแล้ว วรรณคดีเรื่องนี้ก็ยังมีเรื่องอื่นให้น่าสนใจและน่าศึกษาเช่นกัน ถ้าพร้อมแล้วเราไปศึกษาตัวบทและคุณค่าที่แฝงอยู่ในเรื่อง อิเหนา ตอน ศึกกะหมังกุหนิง กันเลยค่ะ ตัวบทเด่น ๆ ในอิเหนา ตอน ศึกกะหมังกุหนิง บทที่ 1 ถอดความ เป็นตอนที่ท้าวกะหมังกุหนิงให้ราชทูตนำสาส์นไปมอบให้ท้าวดาหาเพื่อสู่ขอบุษบาให้วิหยาสะกำ โดยบทนี้เป็นเนื้อหาส่วนหนึ่งที่ท้าวกะหมังกุหนิงเขียนถึงท้าวดาหา โดยเปรียบว่าตนเป็นเหมือนรองเท้าที่จะอยู่เคียงกับท้าวดาหา ดังนั้นจึงจะขอสู่ขอพระธิดาให้กับวิหยาสะกำ

Passive Modals คืออะไร

สวัสดีค่านักเรียนชั้นม.4 ที่น่ารักทุกคน วันนี้เราจะไปดู ” Passive Modals“ ที่ใช้บ่อยพร้อมเทคนิคการใช้งานง่ายๆกันค่า Let’s go! ไปลุยกันเลยเด้อ ทบทวนสักหน่อย ก่อนอื่นเราจะต้องทบทวนเรื่อง Modal verbs หรือ Modal Auxiliaries กันก่อนจร้า แล้วจากนั้นเราจะไปลงลึกเรื่อง Passive voice หรือโครงสร้างประธานถูกกระทำที่คุ้นหูกันหากใครที่ลืมแล้วก็ไม่เป็นไรน๊า มาเริ่มใหม่ทั้งหมดกันเลยจร้า กลุ่มของ