การแยกตัวประกอบ
การแยกตัวประกอบ ของจำนวนนับใด หมายถึง การเขียนจำนวนนับนั้นในรูปการคูณของ ตัวประกอบเฉพาะ ซึ่งในบทความนี้ได้นำเสนอวิธีการ รวมถึง โจทย์การแยกตัวประกอบ ไว้มากมาย น้องๆสามารถศึกษาเรียนรู้ได้ดวยตนเองโดยที่มีวิธีการแยกตัวประกอบ 2 วิธี ดังนี้
- การแยกตัวประกอบ โดยการคูณ
- การแยกตัวประกอบ โดยการหาร (หารสั้น)
ก่อนอื่นน้องๆมาทบทวน ความหมายของตัวประกอบและจำนวนเฉพาะ กันก่อนนะคะ
จำนวนเฉพาะ คือ จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียง 2 ตัว คือ 1 และตัวมันเอง
ตัวประกอบ ของจำนวนนับใด ๆ คือ จำนวนนับที่หารจำนวนนับนั้นได้ลงตัว
แล้วน้องๆ ทราบหรือไม่ว่า ตัวประกอบเฉพาะ คืออะไร ถ้ายังไม่ทราบ แล้วรู้หรือไม่ว่าตัวประกอบทั้งหมดของ 28 มีจำนวนใดบ้าง
ตัวประกอบทั้งหมดของ 28 คือ 1, 2, 4, 7, 14, 28 จะเห็นได้ชัดว่า จำนวนเฉพาะจากตัวประกอบทั้งหมดของ 28 คือ 2 และ 7 เราเรียก 2 และ 7 ว่า ตัวประกอบเฉพาะ
ต่อไปมาดูตัวอย่าง ตัวประกอบ และ ตัวประกอบเฉพาะ กันนะคะ
ตัวอย่างที่ 1 จงหาตัวประกอบและตัวประกอบเฉพาะของจำนวนต่อไปนี้
- 10
- 36
วิธีทำ 1. ตัวประกอบของ 10 คือ 1, 2, 5, 10
ตัวประกอบเฉพาะของ 10 คือ 2, 5
2. ตัวประกอบของ 36 คือ 1, 2, 3, 4, 6, 9, 12, 18, 36
ตัวประกอบเฉพาะของ 36 คือ 2, 3
จากตัวอย่างที่ผ่านมา สามารถสรุปความหมายของตัวประกอบเฉพาะ ได้ว่า ตัวประกอบเฉพาะ คือ ตัวประกอบที่เป็นจำนวนเฉพาะของจำนวนนับใด ๆ
เมื่อทำความรู้จักกับ ตัวประกอบเฉพาะ แล้ว ต่อไปมาดูวิธีการแยกตัวประกอบทั้ง 2 วิธี กันนะคะ เริ่มที่วิธีแรกกันเลยค่ะ
วิธีที่ 1 การแยกตัวประกอบ โดยการคูณ
วิธีการแยกตัวประกอบโดยการคูณ หรือการเขียนแผนภาพ เริ่มโดยการแยกออกเป็นผลคูณทีละสองจำนวน ในการแยกตัวประกอบ ของจำนวนนับที่มีตัวประกอบหลาย ๆ จำนวน เราอาจหาตัวประกอบทีละสองตัวหลาย ๆ ขั้น จนขั้นสุดท้ายได้ตัวประกอบทุกตัวเป็นตัวประกอบเฉพาะ
ตัวอย่างที่ 2 จงแยกตัวประกอบของ 50 และ 72
วิธีทำ 50 = 2 x 25
= 2 x 5 x 5
72 = 2 x 36
= 2 x 2 x 18
= 2 x 2 x 2 x 9
= 2 x 2 x 2 x 3 x 3
ดังนั้น 50 = 2 x 5 x 5 และ 72 = 2 x 2 x 2 x 3 x 3
นอกจากการแยกตัวประกอบโดยการคูณ ยังมีอีกวิธีที่หนึ่งทำคล้าย ๆ กันคือ การแยกตัวประกอบการเขียนแผนภาพ ดังตัวอย่าง ต่อไปนี้
ตัวอย่างที่ 3 จงแยกตัวประกอบของ 60
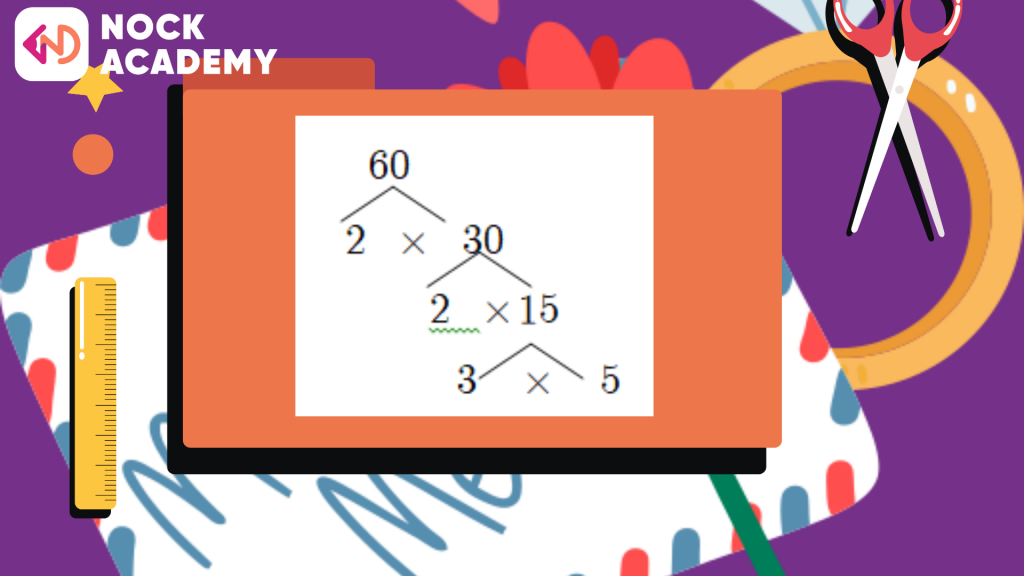ดังนั้น 60 = 2 x 2 x 3 x 5
ตัวอย่างที่ 4 จงแยกตัวประกอบของ 160
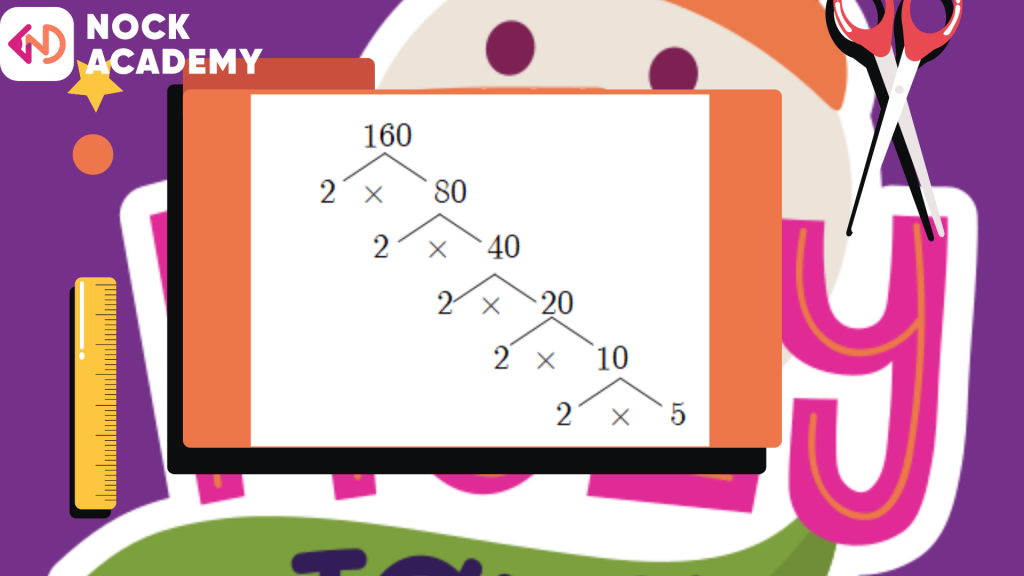
ดังนั้น 160 = 2 x 2 x 2 x 2 x 2 x 5
วิธีการแยกตัวประกอบ โดยการเขียนแผนภาพ เป็นวิธีที่ทำได้ง่ายและรวดเร็ว แต่ถ้าตัวเลขเยอะๆ อาจจะทำให้น้องๆคิดตัวเลขในการแยกตัวประกอบได้ช้า ลำดับต่อไปจึงขอนำเสนอวิธี การแยกตัวประกอบ โดยการหารสั้น
วิธีที่ 2 การแยกตัวประกอบ โดยการหาร (หารสั้น)
วิธีตั้งหาร โดยใช้จำนวนเฉพาะไปหารจำนวนนับที่เป็นตัวตั้งเรื่อย ๆ จนไม่สามารถหารได้ เมื่อนำตัวหารทุกตัวมาคูณกันจะมีค่าเท่ากับจำนวนนับที่กำหนดให้ ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 5 จงแยกตัวประกอบของ 36
วิธีทำ
2 ) 36
2 ) 18
3 ) 9
3
ดังนั้น 36 = 2 x 2 x 3 x 3
ตัวอย่างที่ 6 จงแยกตัวประกอบของ 462
วิธีทำ
2 ) 462
3 ) 231
7 ) 77
11
ดังนั้น 462 = 2 x 3 x 5 x 7 x 11
ตัวอย่างที่ 7 จงแยกตัวประกอบของ 110
วิธีทำ
2 ) 110
5 ) 55
11
ดังนั้น 110 = 2 x 5 x 11
ตัวอย่างที่ 8 จงแยกตัวประกอบของ 80
วิธีทำ
2 ) 80
2 ) 40
2 ) 20
2 ) 10
5
ดังนั้น 80 = 2 x 2 x 2 x 2 x 5
เปรียบเทียบการแยกตัวประกอบ โดยการคูณและการเขียนแผนภาพ
ตัวอย่าง การแยกตัวประกอบ ต่อไปนี้ จะแสดงให้เห็นความแตกต่างอย่างชัดเจน ระหว่างการแยกตัวประกอบโดยการหาร และการแยกตัวประกอบโดยการเขียนแผนภาพ ซึ่งได้รวบรวม โจทย์การแยกตัวประกอบ ไว้หลากหลายโจทย์ เมื่อน้องๆเจอโจทย์การแยกตัวประกอบ จะทำให้น้องๆเลือกวิธีการและทำออกมาได้อย่างถูกต้อง
ตัวอย่างที่ 9 จงแยกตัวประกอบของ 234
ตัวอย่างที่ 10 จงแยกตัวประกอบของ 268
ตัวอย่างที่ 11 จงแยกตัวประกอบของ 290
ตั้งแต่ตัวอย่างที่ 9 ถึง ตัวอย่างที่ 11 น้องๆสังเกตหรือไม่คะ ไม่ว่าจะใช้วิธีการใดในการแยกตัวประกอบ ผลสุดท้ายแล้ว ในการแยกตัวประกอบคำตอบจะได้เท่ากันเสมอ
เมื่อน้องได้เรียนรู้เรื่อง การแยกตัวประกอบ ทั้ง 2 วิธี คือ วิธีการคูณ และ การหาร จำนวนที่นำมาแยกตัวประกอบจะต้องเป็น ตัวประกอบเฉพาะ ซึ่งจาก โจทย์การแยกตัวประกอบ หลายๆข้อ จะเห็นได้ชัดว่า สามารถหาคำตอบได้ง่ายและรวดเร็ว เรื่องต่อไปที่น้องๆต้องเรียนรู้คือการหา ตัวหารร่วมมาก (ห.ร.ม.) ซึ่งจะเป็นการฝึกน้องๆได้มีวิธีการหา ห.ร.ม. แต่ละข้อได้อย่างรวดเร็วและแม่นยำ
คลิปวิดีโอ การแยกตัวประกอบ
คลิปวิดีโอนี้ได้รวบรวมวิธี การแยกตัวประกอบ ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค รวมถึงการอธิบาย โจทย์การแยกตัวประกอบ และสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย
