บทความนี้ได้รวบรวมความรู้เรื่อง สถิติ (เส้นโค้งความถี่)  ซึ่งก่อนที่จะเรียนเรื่องนี้ น้องๆจะต้องมีความรู้ในเรื่อง    ค่ากลางของข้อมูล และการวัดการกระจายของข้อมูล สามารถศึกษาเพิ่มเติมได้ที่  ⇒⇒ สถิติ (ค่ากลางของข้อมูล/การกระจายของข้อมูล) ⇐⇐

เส้นโค้งของความถี่ จะมีอยู่ 3 แบบ คือ เส้นโค้งปกติ เส้นโค้งเบ้ขวา และเส้นโค้งเบ้ซ้าย ซึ่งจะมีความสัมพันธ์กับค่ากลางของข้อมูล  ได้แก่ ค่าเฉลี่ยเลขคณิต (μ)   มัธยฐาน (Med) และฐานนิยม (Mode)  อีกทั้งยังมีความสัมพันธ์กับการกระจายของข้อมูลอีกด้วย

เส้นโค้งปกติหรือรูประฆัง

เส้นโค้งปกติหรือรูประฆัง เป็นเส้นโค้งของความถี่ของข้อมูลที่มีค่าเฉลี่ยเลขคณิต  มัธยฐาน และฐานนิยมเท่ากัน  หรืออยู่ที่จุดเดียวกันคือจุดที่มีความถี่สูงสุด  ดังรูป ซึ่งจะเกี่ยวข้องกับ สถิติ (เส้นโค้งความถี่)

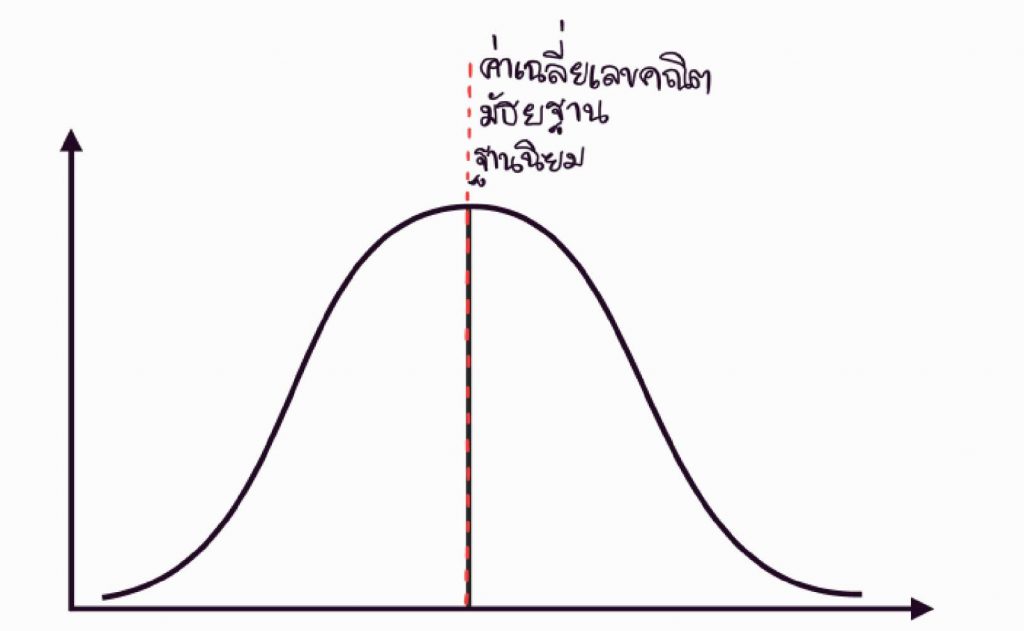
ค่าเฉลี่ยเลขคณิต = มัธยฐาน = ฐานนิยม

เส้นโค้งเบ้ทางขวาหรือทางบวก

เส้นโค้งเบ้ทางขวาหรือทางบวก เป็นเส้นโค้งของความถี่ของข้อมูลที่มีค่ากลางเรียงจากน้อยไปหามาก ฐานนิยม  มัธยฐาน  และค่าเฉลี่ยเลขคณิต  ดังรูป ซึ่งจะเกี่ยวข้องกับ สถิติ (เส้นโค้งความถี่)

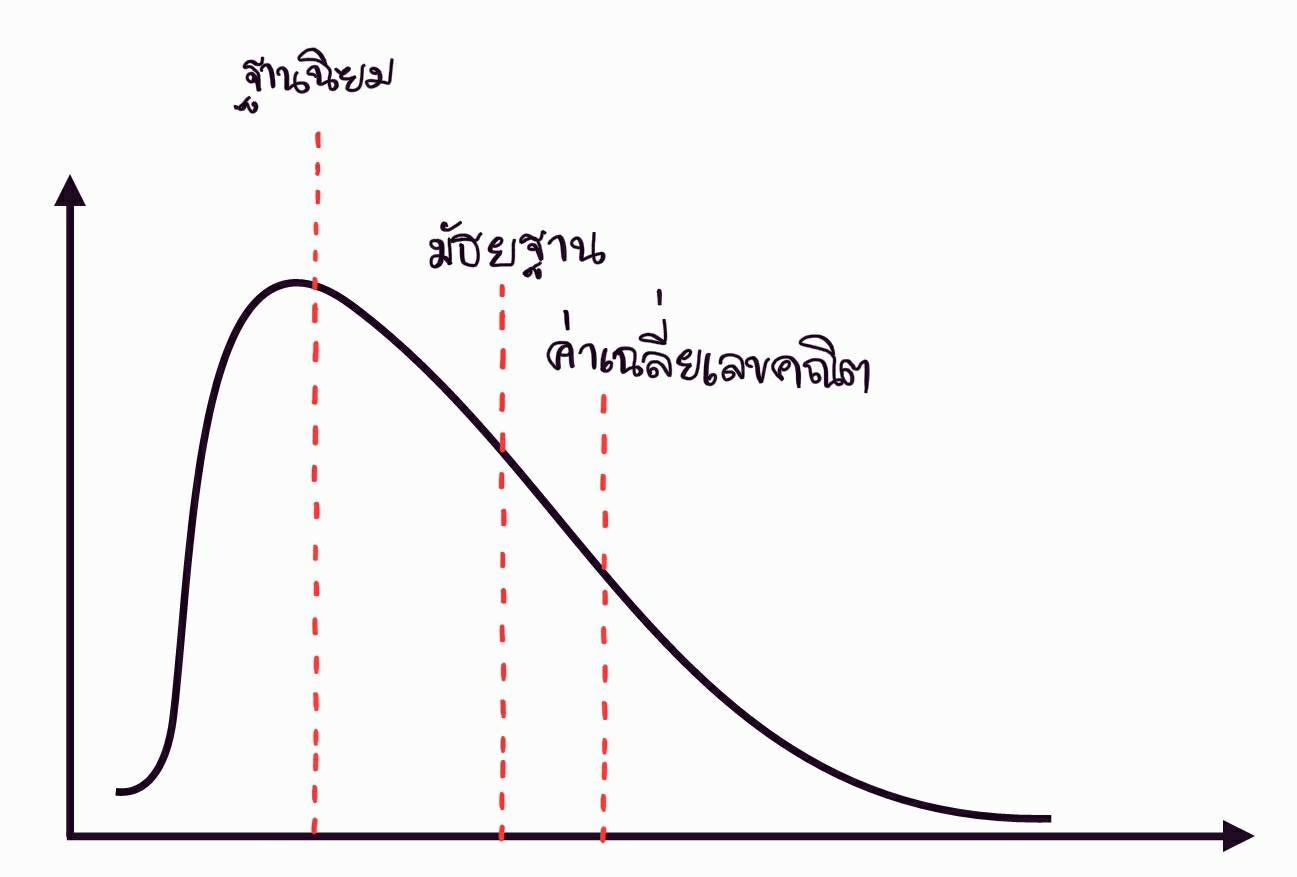
ฐานนิยม  <  มัธยฐาน  <  ค่าเฉลี่ยเลขคณิต

เส้นโค้งเบ้ทางซ้ายหรือทางลบ

เส้นโค้งเบ้ทางซ้ายหรือทางลบ เป็นเส้นโค้งของความถี่ของข้อมูลที่มีค่ากลางเรียงจากน้อยไปหามาก   ค่าเฉลี่ยเลขคณิต  มัธยฐาน  และฐานนิยม  ดังรูป ซึ่งจะเกี่ยวข้องกับ สถิติ (เส้นโค้งความถี่)

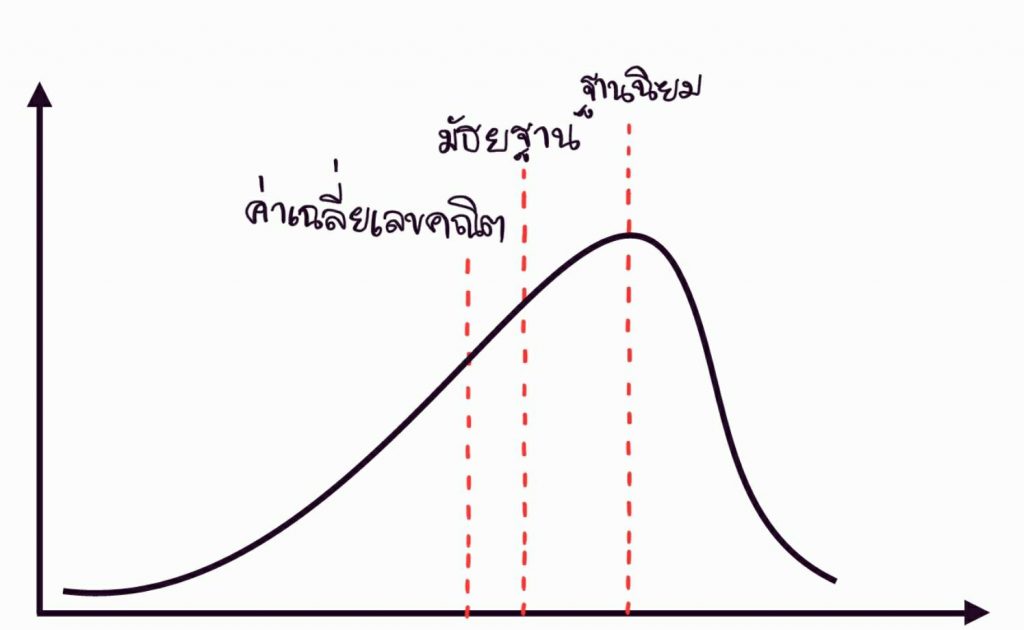
ค่าเฉลี่ยเลขคณิต  <  มัธยฐาน  <  ฐานนิยม

สรุป

• เส้นโค้งปกติ ⇒ ค่าเฉลี่ยเลขคณิต = มัธยฐาน = ฐานนิยม
• เส้นโค้งเบ้ทางขวา ⇒ ฐานนิยม  <  มัธยฐาน  <  ค่าเฉลี่ยเลขคณิต (ค่าเฉลี่ยเลขคณิตมากที่สุด)
• เส้นโค้งเบ้ทางซ้าย ⇒ ค่าเฉลี่ยเลขคณิต  <  มัธยฐาน  <  ฐานนิยม (ฐานนิยมมากที่สุด)

การกระจายของข้อมูลเส้นโค้งปกติ

สำหรับการกระจายของข้อมูลนั้น  เมื่อเขียนเป็น เส้นโค้งความถี่  ซึ่งเป็นโค้งปกติ ข้อมูลชุดใดมีการกระจายมาก  เส้นโค้งปกติจะมีความโด่งน้อยหรือค่อนข้างแบน  แต่ถ้าข้อมูลใดมีการกระจายน้อย  เส้นโค้งปกติจะมีความโด่งมาก  ดังรูป

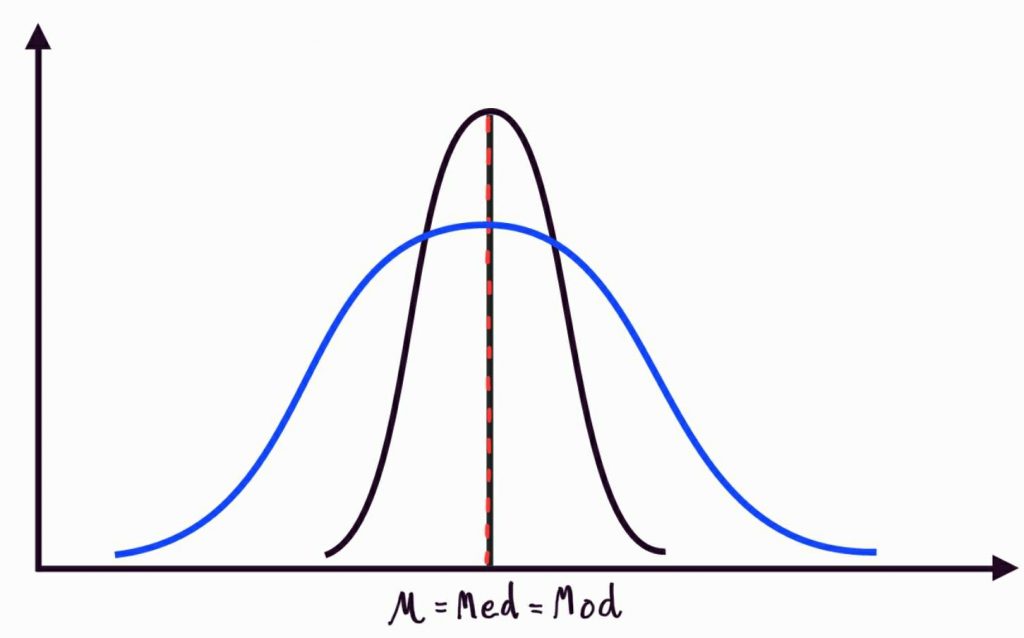
เส้นโค้งที่มีค่าเฉลี่ยเลขคณิตเท่ากัน แต่การกระจายต่างกัน

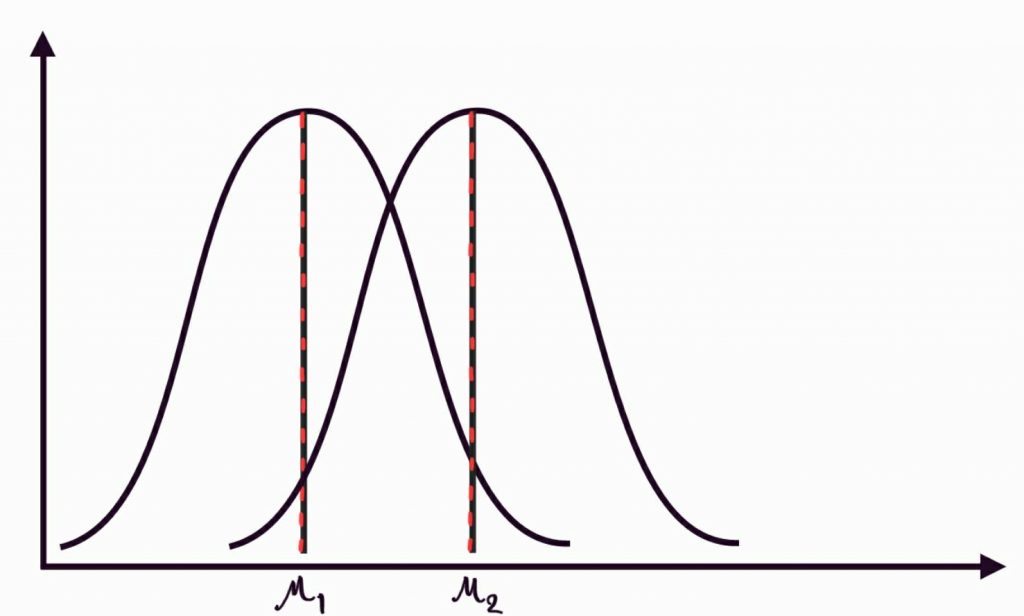
เส้นโค้งที่มีค่าเฉลี่ยเลขคณิตต่างกัน แต่การกระจายเท่ากัน

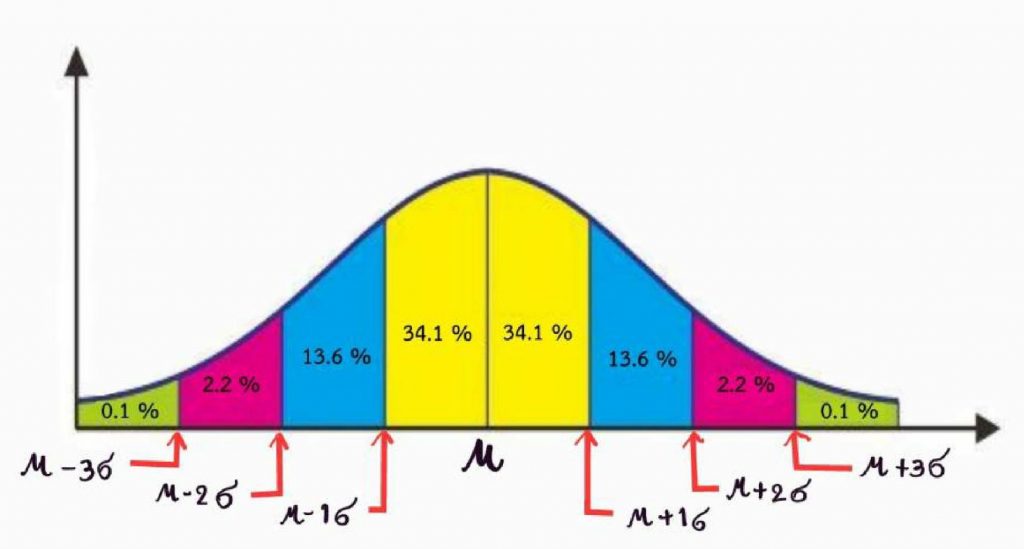
µ  คือ ค่าเฉลี่ยเลขคณิต (µ อ่านว่า มิว)

σ คือ ส่วนเบี่ยงเบนมาตรฐาน (σ อ่านว่า ซิกมา)

โดยที่ พื้นที่ใต้เส้นโค้งปกติจะเป็นดังรูปด้านบนเสมอ คือ 0.1%, 2.2%, 13.6% และ 34.1% ซึ่งพื้นที่ใต้เส้นโค้งปกติครึ่งหนึ่ง จาก µ ไปทางซ้าย หรือจาก µ ไปทางขวา จะมีพื้นที่ใต้เส้นโค้งเท่ากับ 50%

พิจารณาข้อความที่กำหนดให้ต่อไปนี้

กำหนดให้ µ = 30, σ = 4 จงหา μ – 1σ ,  μ – 2σ ,  μ – 3σ ,  μ + 1σ , μ + 2σ , μ + 3σ  และเติมลงในเส้นโค้งปกติ

หา μ – 1σ = 30 – 1(4) = 30 – 4 = 26

หา μ – 2σ = 30 – 2(4) = 30 – 8 = 22

หา μ – 3σ = 30 – 3(4) = 30 – 12 = 18

หา μ + 1σ = 30 + 1(4) = 30 + 4 = 34

หา μ + 2σ = 30 + 2(4) = 30 + 8 = 38

หา μ + 3σ = 30 + 3(4) = 30 + 12 = 42

เขียนเส้นโค้งปกติ ได้ดังนี้

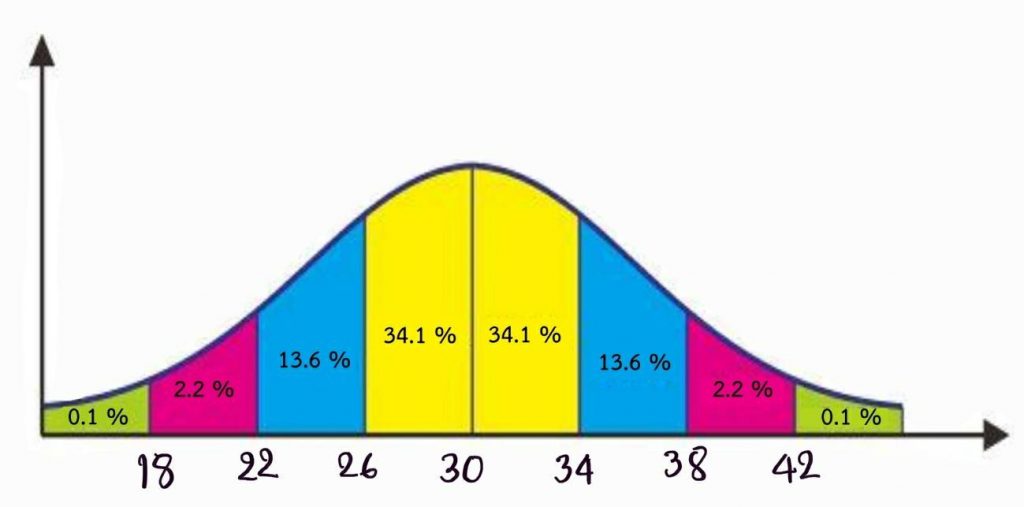
ตัวอย่างที่ 1

ตัวอย่างที่ 1  ในการตรวจสอบอายุการใช้งานของแบตเตอรี่มือถือยี่ห้อหนึ่งต่อการชาร์จไฟหนึ่งครั้ง พบว่ามีการแจกแจงปกติ มีค่าเฉลี่ยเลขคณิตเท่ากับ 100 ชั่วโมง และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 12 ชั่วโมง  จงหาค่าของข้อมูล

1)  แบตเตอรี่มือถือที่มีอายุการใช้งานระหว่าง 112 – 124 ชั่วโมงมีกี่เปอร์เซ็นต์

2)  แบตเตอรี่มือถือที่มีอายุการใช้งานน้อยกว่า 88 ชั่วโมงมีกี่เปอร์เซ็นต์

3)  แบตเตอรี่มือถือที่มีอายุการใช้งานระหว่าง  88 – 112 ชั่วโมงมีกี่เปอร์เซ็นต์

วิธีทำ     เนื่องจากแบตเตอรี่มือถือมีการแจกแจงปกติค่าเฉลี่ยเลขคณิต เท่ากับ 100 ชั่วโมง  ส่วนเบี่ยงเบนมาตรฐาน เท่ากับ 12 ชั่วโมง

อธิบายเพิ่มเติม : μ = 100, σ = 12 (เนื่องจากเส้นโค้งปกติเราจะเขียน μ = 100 ไว้ตรงกลาง ตามรูปด้ายล่าง)

หา μ – 1σ = 100 – 1(12) =100 – 12 = 88

หา μ – 2σ = 100 – 2(12) =100 – 24 = 76

หา μ – 3σ = 100 – 3(12) =100 – 36 = 64

หา μ + 1σ = 100 + 1(12) =100 + 12 = 112

หา μ + 2σ = 100 + 2(12) =100 + 24 = 124

หา μ + 3σ = 100 + 3(12) =100 + 36 = 136

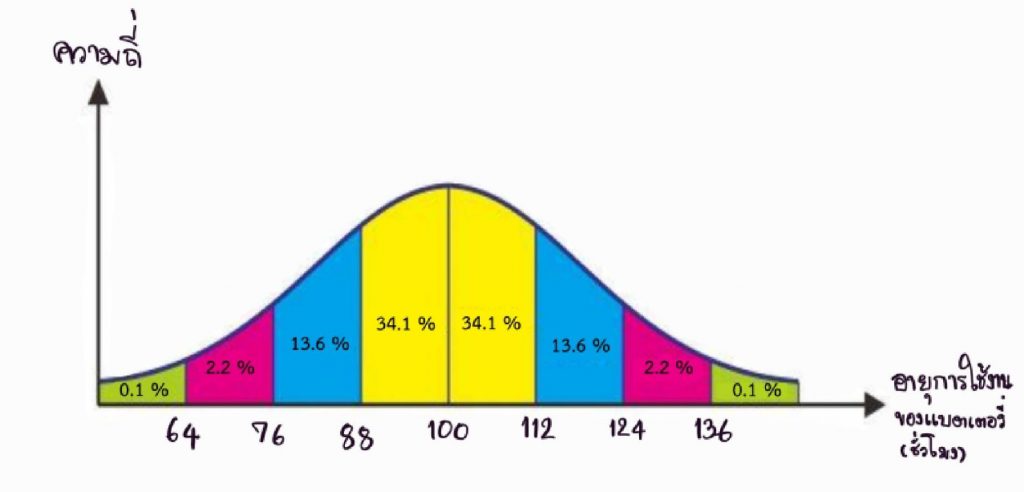
1)  แบตเตอรี่มือถือที่มีอายุการใช้งานระหว่าง 112 – 124 ชั่วโมง มี 13.6 %

2)  แบตเตอรี่มือถือที่มีอายุการใช้งานน้อยกว่า 88 ชั่วโมงมี 50% – 34.1% = 15.9% หรือ 0.1% + 2.2% + 13.6% = 15.9%

3)  แบตเตอรี่มือถือที่มีอายุการใช้งานระหว่าง  88 – 112 ชั่วโมงมี 34.1% + 34.1% = 68.2%

ตัวอย่างที่ 2

ตัวอย่างที่ 2  ในการแข่งขันตอบคำถามคณิตศาสตร์ระดับประเทศระดับชั้นมัธยมศึกษาปีที่ 3 มีนักเรียนเข้าร่วมแข่งขัน 1,200 คน ค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบเป็น 49 และ 7 คะแนน ตามลำดับ จงหา

1)  นักเรียนที่สอบได้คะแนนน้อยกว่า 56 คะแนน คิดเป็นกี่เปอร์เซ็นต์และมีประมาณกี่คน

2)  นักเรียนที่สอบได้คะแนนระหว่าง 35 และ 56 คะแนน คิดเป็นกี่เปอร์เซ็นต์และมีประมาณกี่คน

3)  นักเรียนที่สอบได้คะแนนมากกว่า 42 คะแนน คิดเป็นกี่เปอร์เซ็นต์และมีประมาณกี่คน

วิธีทำ     เนื่องจากค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบเป็น 45 และ 7คะแนน ตามลำดับ

อธิบายเพิ่มเติม : μ = 49, σ = 7 (เนื่องจากเส้นโค้งปกติเราจะเขียน μ = 49 ไว้ตรงกลาง ตามรูปด้ายล่าง)

หา μ – 1σ = 49 – 1(7) = 49 – 7 = 42

หา μ – 2σ = 49 – 2(7) = 49 – 14 = 35

หา μ – 3σ = 49 – 3(7) = 49 – 21 = 28

หา μ + 1σ = 49 + 1(7) = 49 + 7 = 56

หา μ + 2σ = 49 + 2(7) = 49 + 14 = 63

หา μ + 3σ = 49 + 3(7) = 49 + 21 = 70

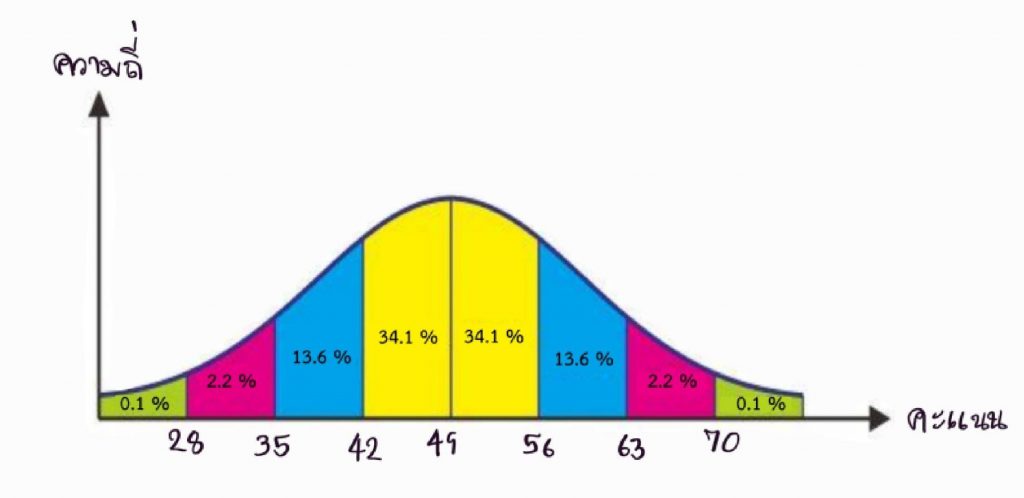
1)  นักเรียนที่สอบได้คะแนนน้อยกว่า 56 คะแนน คิดเป็น 50% + 34.1% = 84.1%  มีประมาณ    x 1,200 ≈ 1,010  คน

2)  นักเรียนที่สอบได้คะแนนระหว่าง 35 และ 56 คะแนน คิดเป็น 13.6% + 34.1% + 34.1%  = 81.8%

และมีประมาณ   x 1,200 ≈ 982  คน

3)  นักเรียนที่สอบได้คะแนนมากกว่า 42 คะแนน คิดเป็น 34.1% + 50% = 84.1% มีประมาณ    x 1,200 ≈ 1,010  คน

เมื่อน้องๆเรียนรู้เรื่อง สถิติ (เส้นโค้งความถี่) จะทำให้น้องๆสามารถตอบเขียนเส้นโค้งปกติและตอบคำถามได้ถูกต้อง โดยสามารถนำความรู้ที่ได้จากการเรียนเรื่องเส้นโค้งความถี่ มาประยุกต์ใช้ในการแก้โจทย์ปัญหาและหาคำตอบได้อย่างถูกต้อง

วิดีโอ เส้นโค้งปกติ

        คลิปวิดีโอนี้ได้รวบรวม วิธีแก้ปัญหาโดยใช้เส้นโค้งปกติ และนอกจากนี้ยังได้แนะนำให้รู้จักกับเส้นโค้งเบ้ขวา และเส้นโค้งเบ้ซ้าย ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค ที่จะทำให้น้องๆมองวิชาคณิตศาสตร์เป็นเรื่องง่าย