ฟังก์ชันตรีโกณมิติของมุม

ฟังก์ชันตรีโกณมิติของมุม จะเกี่ยวข้องกับมุมที่มีหน่วยเป็นองศา (degree) และมุมที่มัหน่วยเป็นเรเดียน (radian)

ในบทความนี้จะกล่าวถึงมุมทั้งหน่วยองศาและเรเดียน มุมฉาก การเปลี่ยนหน่วยของมุม สมบัติของฟังก์ชันตรีโกณมิติ และสามเหลี่ยมมุมฉาก

ก่อนที่จะเริ่มเข้าสู่เนื้อหา พี่อยากให้น้องๆได้รู้พื้นฐานเกี่ยวกับฟังก์ชันตรีโกณมิติเพื่อที่จะได้เข้าใจเนื้อหาในบทความนี้มากขึ้น

• การวัดความยาวส่วนโค้ง
• ค่าของฟังก์ชันไซน์และโคไซน์
• ฟังก์ชันตรีโกณมิติอื่นๆ

หลังจากที่ไปทบทวนความรู้มาแล้วเรามาเริ่มเนื้อหาใหม่กันเลยค่ะ

หน่วยของมุม

1.) องศา (degree) คือหน่วยของมุมในระนาบ 2 มิติ โดยที่

1 มุมฉาก = 90°

1°            = 60′ (ลิปดา)

1′            = 60″ (ฟิลิปดา)

มุมฉากที่น้องๆคุ้นกัน ก็คือ สามเหลี่ยมมุมฉาก

2.) เรเดียน (radian) คือหน่วยวัดมุมบนระนาบ 2 มิติ

มุม 1 เรเดียน คือขนาดของมุมที่วัดจากจุดศูนย์กลางของวงกลมที่กางออกตามส่วนโค้ง ซึ่งความยาวส่วนโค้งมีความยาวเท่ากับรัศมีของวงกลมพอดี

 

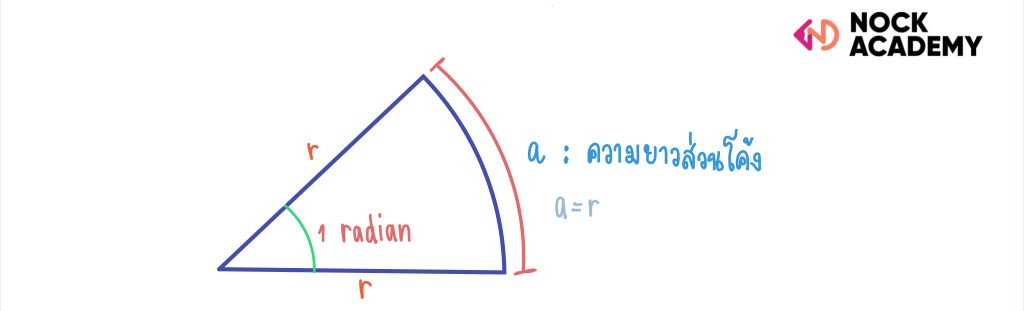
ดังนั้น มุม θ =

 

 

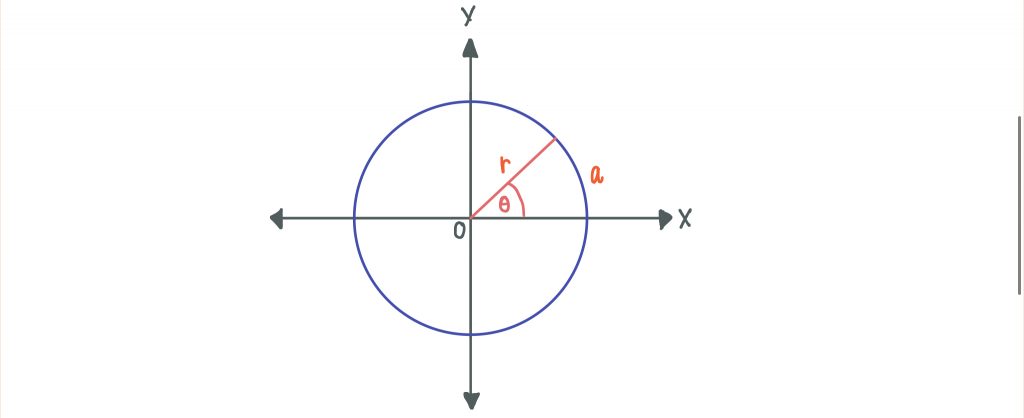
ดังนั้นถ้าเราหมุนรัศมีครบ 1 รอบ จะได้ว่า นั่นคือ θ = เรเดียน

จากนั้นเรามาพิจารณามุมฉาก (90°) ซึ่ง

ดังนั้น 90° =     ⇒    180° =

ตัวอย่างการเปลี่ยนหน่วยของมุม

• 5 เรเดียน เปลี่ยนเป็นองศา

จาก = 180° ดังนั้น 5 = 5(180) = 900°

• เรเดียน เปลี่ยนเป็นองศา

จะได้  = = 240°

• 780° เปลี่ยนเป็นเรเดียน

ใช้วิธีเทียบสัดส่วน คือ

180° =

780° = =

• -330° เปลี่ยนเป็นเรเดียน

จะได้ =

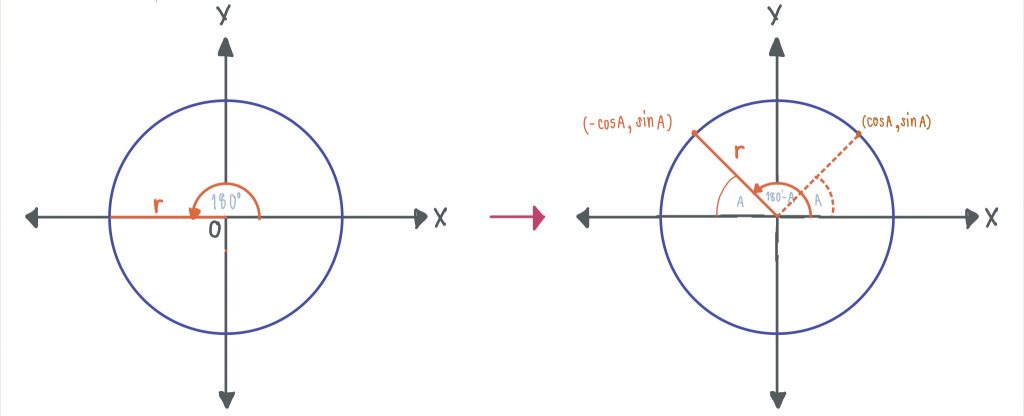
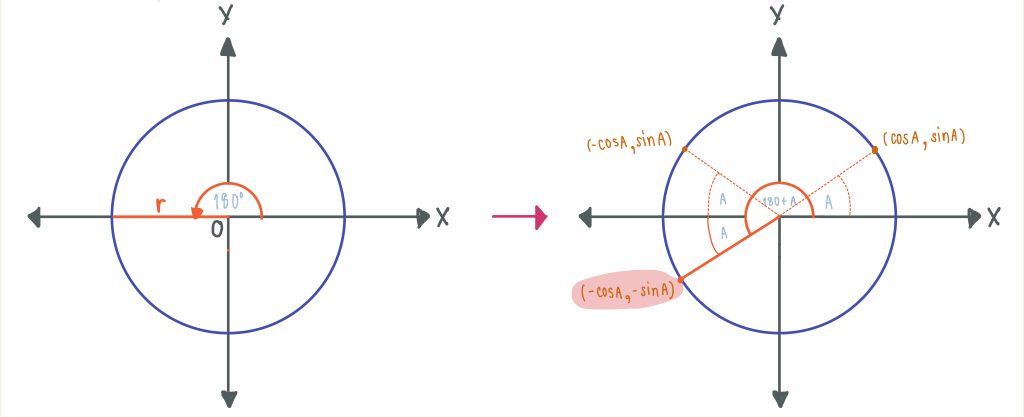
ฟังก์ชันตรีโกณมิติของมุม 180° ± A, 360±A และ (-A) เมื่อ 0 < A < 90°

sin(180° – A) = sinA                      cosec(180° – A) = cosecA

cos(180° – A) = -cosA                   sec(180° – A) = -secA

tan(180° – A) = -tanA                   cot(180° – A) = -cotA

————————————————————————————————

sin(180° + A) = -sinA                      cosec(180° + A) = -cosecA

cos(180° + A) = -cosA                   sec(180° + A) = -secA

tan(180° + A) = tanA                   cot(180° + A) = cotA

————————————————————————————————

sin(360° + A) = sinA                      cosec(360° + A) = cosecA

cos(360° + A) = cosA                   sec(360° + A) = secA

tan(360° + A) = tanA                   cot(360° + A) = cot

————————————————————————————————

sin(360° – A) = -sinA                      cosec(360° – A) = -cosecA

cos(360° – A) = cosA                      sec(360° – A) = secA

tan(360° – A) = -tanA                   cot(360° – A) = -cot
————————————————————————————————
sin(-A) = -sinA                             cosec(-A) = -cosecA

cos(-A) = cosA                             sec(-A) = secA

tan(-A) = -tanA                           cot(-A) = -cotA

ฟังก์ชันตรีโกณมิติของมุม ของรูปสามเหลี่ยมมุมฉาก

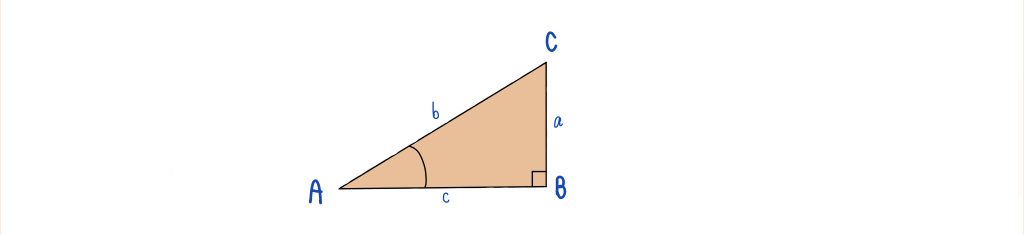
A, B และ C เป็นมุมของสามเหลี่ยม

ในรูปนี้จะพิจารณามุม A

a แทนความยาวด้านตรงข้ามมุม A ⇒ ข้าม

b แทนความยาวด้านประชิดมุม A ⇒ ชิด

c แทนความยาวด้านตรงข้ามมุมฉาก ⇒ ฉาก

จากรูปจะได้ว่า

sinA = ข้าม/ฉาก =

cosA = ชิด/ฉาก =

tanA = ข้าม/ชิด =

 

ตัวอย่าง

ให้ cosθ =  และ ≤ θ ≤

ขั้นแรกเราจะพิจารณาเงื่อนไขที่โจทย์ให้มา นั่นก็คือ ≤ θ ≤

ซึ่งจากเงื่อนไขนี้สามารถบอกได้ว่าเรากำลังพิจารณาค่าของฟังก์ชันตรีโกณที่อยู่ใน ควอดรันต์ที่ 2

ดังนั้น sinθ, cosecθ มีค่าเป็นบวก tanθ, cotθ และ secθ มีค่าเป็นลบ

จาก cosθ =  = ชิด/ฉาก เราจะวาดรูปได้ดังนี้

หา a โดยใช้ทฤษฎีบทพีทาโกรัส

c² = a² + b²

25 = a² + 9

a² = 16

a = ±4

จาก a คือความยาว ดังนั้น a = 4

ดังนั้น sinθ =

tanθ =

cotθ =

secθ =

cosecθ =

การหาขนาดของมุมจากรูปสามเหลี่ยมมุมฉาก

ถ้าเรามีรูปสามเหลี่ยมที่บอกความยาวด้านมา เราสามารถหามุมได้โดยใช้ข้อมูลเหล่านั้นช่วย

เช่น

1)

จากรูปจะเห็นว่าบอกความความยาวด้านชิดมุมA และด้านตรงข้ามมุมฉาก

นั่นคือ รู้ชิด รู้ฉาก  ดังนั้นเราจะหามุมจากฟังก์ชันcos

cosA = =  =

ดังนั้น A = 45°

2)

จากรูป เรารู้ความยาวด้านชิดมุมA และด้านตรงข้ามมุมA

ดังนั้นจะหาโดยใช้ tanA = =

ดังนั้น A = 60°

มุมอื่นๆที่ควรรู้

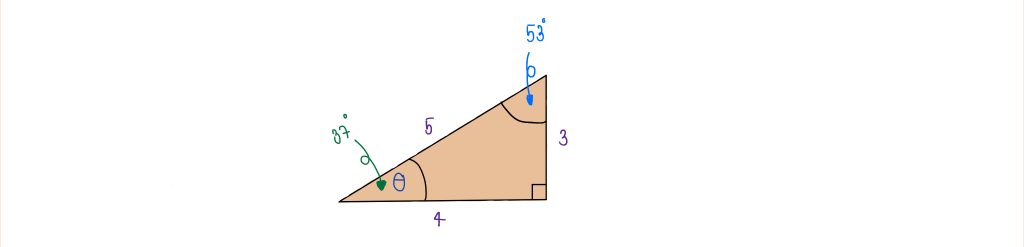
มุม A = 35 จะได้ sin35° =  และ cos35° =

มุมA = 53 จะได้ sin53° = และ cos53° =

วิดีโอเพิ่มเติม