ความน่าจะเป็นกับการตัดสินใจ

บทความนี้ได้รวบรวมความรู้เรื่อง ความน่าจะเป็นกับการตัดสินใจ สำหรับบางเหตุการณ์ความรู้เรื่องความน่าจะเป็นเพียงอย่างเดียว  อาจไม่เพียงพอที่จะช่วยตัดสินใจได้  จำเป็นจะต้องหาองค์ประกอบอื่นมาช่วยในการตัดสินใจด้วย  นั่นคือผลตอบแทนของการเกิดเหตุการณ์นั้น ซึ่งก่อนที่จะเรียนเรื่องนี้ น้องๆจะต้องมีความรู้ในเรื่อง ความน่าจะเป็นของเหตุการณ์ สามารถศึกษาเพิ่มเติมได้ที่  ⇒⇒ ความน่าจะเป็นของเหตุการณ์ ⇐⇐

ผลตอบแทนของเหตุการณ์อาจหมายถึง ผลตอบแทนที่ได้หรือผลตอบแทนที่เสีย  เช่น  ในการเล่นแทงหัวก้อย  ถ้าออกหัว พีชจะได้เงิน 2 บาท และถ้าออกก้อย พอลจะต้องเสียเงิน 3 บาท เงิน 2 บาทที่พอลจะได้รับเป็นผลตอบแทนที่ได้  แทนด้วย +2  และเงิน 3 บาทที่พีชจะต้องเสียเป็นผลตอบแทนที่เสีย  แทนด้วย -3

ค่าคาดหมาย  หมายถึง การนำความน่าจะเป็นของเหตุการณ์และผลตอบแทนของการเกิดเหตุการณ์นั้นมาพิจารณาประกอบกันในทางสถิติ ซึ่งหาได้จาก ผลรวมของผลคูณระหว่างความน่าจะเป็นของเหตุการณ์กับผลตอบแทนของเหตุการณ์

ตัวอย่างที่ 1 

ตัวอย่างที่ 1   ในงานเลี้ยงแห่งหนึ่งอานนท์และธีรเทพนั่งโต๊ะเดียวกัน ในระหว่างนั่งรออาหารนั้น  อานนท์หยิบเหรียญบาทออกมาสองเหรียญ  แล้วท้าพนันธีรเทพโดยมีกติกาว่า  ให้อานนท์โยนเหรียญ 2 เหรียญ  พร้อมกัน 1 ครั้ง ถ้าเหรียญที่โยนออกก้อยทั้งคู่แล้วอานนท์จะจ่ายให้ธีรเทพ 5 บาท แต่ถ้าเหรียญออกเป็นอย่างอื่นธีรเทพต้องจ่ายให้อานนท์ 3 บาท  ถ้ามีการพนันโยนเหรียญกันแบบนี้ไปเรื่อย ๆ หลาย ๆ ครั้ง  จงหาค่าคาดหมายที่ธีรเทพจะได้เงินในครั้งนี้  และคิดว่าใครจะได้เงินมากกว่ากัน

วิธีทำ     ในการโยนเหรียญบาทที่เที่ยงตรง 2 เหรียญพร้อมกัน 1 ครั้ง  ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้มี 4 แบบ คือ HH, TT, HT หรือ TH

ความน่าจะเป็นของเหตุการณ์ที่เหรียญออกก้อยทั้งคู่ เท่ากับ 

ความน่าจะเป็นของเหตุการณ์ที่เหรียญไม่ออกก้อยทั้งคู่ เท่ากับ 

เนื่องจากแต่ละครั้งที่อานนท์โยนเหรียญ ถ้าเหรียญที่โยนออกเป็น TT อานนท์จะจ่ายเงินให้ธีรเทพ 5 บาท

ดังนั้น ผลตอบแทนของเหตุการณ์เป็นการที่ธีรเทพได้เงิน 5 บาท จึงแทนด้วย +5

เนื่องจากแต่ละครั้งที่โยนเหรียญ ถ้าเหรียญที่โยนไม่ออก TT ธีรเทพต้องจ่ายเงินให้อานนท์ 3 บาท

ดังนั้น ผลตอบแทนของเหตุการณ์เป็นการที่ธีรเทพเสียเงิน 3 บาท จึงแทนด้วย -3

การพนันโยนเหรียญหนึ่งครั้งค่าคาดหมายของธีรเทพ เป็นดังนี้

ค่าคาดหมาย =  (ผลตอบแทนที่ได้ × ความน่าจะเป็นของเหตุการณ์ที่เหรียญออกก้อยทั้งคู่)                                                          + (ผลตอบแทนที่เสีย × ความน่าจะเป็นของเหตุการณ์ที่เหรียญไม่ออกก้อยทั้งคู่)

    = (5 × ¹⁄₄) + (-3 × ³⁄₄)

    = ⁵⁄₄ + (-9⁄₄)

    = -⁴⁄₄

    = -1

นั่นคือ ค่าคาดหมายของธีรเทพ เท่ากับ -1 บาท

แสดงว่า ถ้ามีการพนันโยนเหรียญกันแบบนี้ไปเรื่อย ๆ หลาย ๆ ครั้ง โดยเฉลี่ยธีรเทพเสียเงินครั้งละ 1 บาท หรือกล่าวได้ว่า อานนท์ได้เงินมากกว่าธีรเทพ

ตัวอย่างที่ 2

ตัวอย่างที่ 2   จากตัวอย่างที่ 1 ถ้าการพนันโยนเหรียญสองเหรียญ เปลี่ยนกติกาเป็นดังนี้ให้อานนท์โยนเหรียญ 2 เหรียญพร้อมกัน 1 ครั้ง ถ้าเหรียญที่โยนออกหัวทั้งคู่ แล้วธีรเทพจะจ่ายเงินให้อานนท์ 3 บาท แต่ถ้าเหรียญออกอย่างอื่น อานนท์ต้องจ่ายให้ธีรเทพ 1 บาท ถ้าโยนเหรียญไปเรื่อย ๆ หลาย ๆ ครั้งใครจะได้เงินมากกว่ากัน

วิธีทำ     การพนันโยนเหรียญหนึ่งครั้ง จะมีค่าคาดหมายของธีรเทพเปลี่ยนแปลงเป็นดังนี้

ค่าคาดหมาย = (ผลตอบแทนที่ได้ × ความน่าจะเป็นของเหตุการณ์ที่เหรียญออกหัวทั้งคู่)                                                            + (ผลตอบแทนที่เสีย × ความน่าจะเป็นของเหตุการณ์ที่เหรียญไม่ออกหัวทั้งคู่)

    = (1 × ³⁄₄) + (-3 × ¹⁄₄)

    = ³⁄₄ + (⁻³⁄₄)

    = 0

นั่นคือ ค่าคาดหมายของธีรเทพเท่ากับ 0 บาท

แสดงว่า  ถ้ามีการพนันโยนเหรียญกันแบบนี้ไปเรื่อย ๆ หลาย ๆ ครั้ง โดยเฉลี่ยทั้งอานนท์และธีรเทพจะเสมอตัว ไม่มีใครได้เงินมากกว่ากัน

ตัวอย่างที่ 3 

ตัวอย่างที่ 3   ในรายการเกมเศรษฐี  ลลิตาต้องตอบคำถามข้อสุดท้ายมี 4 ตัวเลือก หากตอบถูกจะได้เงิน 100,000 บาท ตอบผิดจะได้เงิน 5,000 บาท ถ้าไม่ตอบจะได้เงิน 10,000 บาท ลลิตาใช้ตัวช่วยหมดแล้ว และไม่ทราบคำตอบเลย  ถ้านักเรียนเป็นลลิตานักเรียนจะตอบคำถามหรือหยุดเล่น

วิธีทำ     ในการตอบคำถาม 4 ตัวเลือก 1 ข้อ จะมีข้อถูก 1 ข้อและข้อผิด 3 ข้อ

ความน่าจะเป็นของเหตุการณ์ที่จะตอบถูก  เท่ากับ 

ความน่าจะเป็นของเหตุการณ์ที่จะตอบผิด  เท่ากับ

เนื่องจาก ถ้าลลิตาตอบถูกลลิตาจะได้เงิน 100,000 บาท

ดังนั้น ผลตอบแทนของเหตุการณ์ที่ลลิตาได้เงิน 100,000 บาท จึงแทนด้วย +100000

เนื่องจาก ถ้าลลิตาตอบผิดลลิตาจะเสียเงิน 5,000 บาท

ดังนั้น ผลตอบแทนของเหตุการณ์ที่ลลิตาเสียเงิน 5000 บาท จึงแทนด้วย -5000

เนื่องจาก ถ้าลลิตาไม่ตอบลลิตาจะได้เงิน 10,000 บาท

ดังนั้น ผลตอบแทนของเหตุการณ์ที่ลลิตาได้เงิน 10,000 บาท จึงแทนด้วย +10000

การตอบคำถามข้อสุดท้าย ค่าคาดหมายของลลิตา เป็นดังนี้

ค่าคาดหมาย  = (ผลตอบแทนที่ได้ × ความน่าจะเป็นของเหตุการณ์ที่จะตอบคำถามถูก)                                                              + (ผลตอบแทนที่เสีย × ความน่าจะเป็นของเหตุการณ์ที่ตอบคำถามผิด)

    = (100,000 × ¹⁄₄) + (-5,000 × ³⁄₄)

    = ¹⁰⁰⁰⁰⁰⁄₄ + (⁻¹⁵⁰⁰⁰⁄₄)

    = ⁸⁵⁰⁰⁰⁄₄

    = 21,250

นั่นคือ ค่าคาดหมายของลลิตา เท่ากับ 21,250 บาท

แสดงว่า ลลิตาควรเล่นต่อไป

ตัวอย่างที่ 4 

ตัวอย่างที่ 4  แป้นวงกลมปาเป้าผู้เล่นจะเสียค่าเล่นครั้งละ  20 บาท  โดยมีรางวัล  ดังนี้

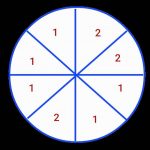
ถ้าปาโดนหมายเลข 1 จะไม่ได้รับเงิน

ถ้าปาโดนหมายเลข 2 จะได้รับเงิน 100 บาท

ถ้าพิมพ์เล่นแป้นวงกลมปาเป้า จงหาว่าแต่ละครั้งที่พิมพ์เล่นมีค่าคาดหมายที่จะได้รับเงินเป็นเท่าใด

วิธีทำ     จำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมดเท่ากับ 8

จำนวนเหตุการณ์ที่จะปาเป้าโดนหมายเลข  1 เท่ากับ 6

ความน่าจะเป็นที่พิมพ์จะปาเป้าโดนหมายเลข 1 เท่ากับ ⁶⁄₈ = ³⁄₄

จำนวนเหตุการณ์ที่จะปาเป้าโดนหมายเลข 2 เท่ากับ 2

ความน่าจะเป็นที่พิมพ์จะปาเป้าโดนหมายเลข 2 เท่ากับ ²⁄₈ = ¹⁄₄

ผลตอบแทนที่ได้เท่ากับ 100

ผลตอบแทนที่เสียเท่ากับ -20

ค่าคาดหมาย  = (ผลรวมของผลคูณระหว่างความน่าจะเป็นของเหตุการณ์กับผลตอบแทนของเหตุการณ์)

    = (¹⁄₄ × 100) + (³⁄₄ × (-20)) 

                         = ¹⁰⁰⁄₄ – ⁶⁰⁄₄

                            = 25 – 15

     = 10

               ดังนั้น พิมพ์เล่นแป้นวงกลมปาเป้า พิมพ์มีค่าคาดหมายที่จะได้รับเงิน เท่ากับ 10

ตัวอย่างที่ 5

ตัวอย่างที่ 5  ในการจัดงานวัดแห่งหนึ่ง  พ่อค้าได้นำวงล้อเสี่ยงโชคเพื่อการกุศล มีตัวเลข 1 – 8 เรียงกันตามช่องที่แบ่งเท่ากันบนแป้นวงกลม  และมีลูกศรชี้ช่องตัวเลข ดังรูป มาให้ลูกค้าหมุนเสี่ยงโชค  โดยมีกติกาว่า ถ้าลูกค้าหมุนเสี่ยงโชคหนึ่งครั้ง ถ้าลูกศรชี้ที่ตัวเลข 2 หรือ 4 แล้ว ทางพ่อค้าจะจ่ายเงินให้ลูกค้า 100 บาท และแต่ละครั้งที่หมุนวงล้อ ลูกค้าต้องจ่ายเงินซื้อตั๋วหนึ่งใบราคา 50 บาท ถ้ามดดำซื้อตั๋วหมุนวงล้อเสี่ยงโชคหนึ่งใบ จงตอบคำถามต่อไปนี้

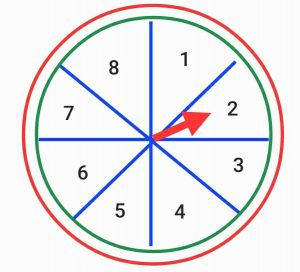
1) ความน่าจะเป็นของเหตุการณ์ที่มดดำจะได้รับรางวัลเป็นเท่าไร

2) ความน่าจะเป็นของเหตุการณ์ที่มดดำจะไม่ได้รับรางวัลเป็นเท่าไร

3) การหมุนวงล้อเสี่ยงโชคหนึ่งครั้ง ค่าคาดหมายที่มดดำจะได้เงินเป็นเท่าไร และหมายความว่าอย่างไร จงอธิบาย

วิธีทำ    1) ความน่าจะเป็นของเหตุการณ์ที่มดดำจะได้รับรางวัลเป็นเท่าไร

ในการหมุนวงล้อเสี่ยงโชคหนึ่งครั้ง  ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้มี 8 แบบ คือ 1, 2, 3, 4, 5, 6, 7 , 8

ความน่าจะเป็นของเหตุการณ์ที่มดดำจะได้รับรางวัล  เท่ากับ ²⁄₈  หรือ ¹⁄₄ 

     2) ความน่าจะเป็นของเหตุการณ์ที่มดดำจะไม่ได้รับรางวัลเป็นเท่าไร

     ความน่าจะเป็นของเหตุการณ์ที่มดดำจะไม่ได้รับรางวัล  เท่ากับ ⁶⁄₈  หรือ ³⁄₄

     3) การหมุนวงล้อเสี่ยงโชคหนึ่งครั้ง ค่าคาดหมายที่มดดำจะได้เงินเป็นเท่าไร และหมายความว่าอย่างไรจงอธิบาย

               เนื่องจาก ถ้ามดดำหมุนเสี่ยงโชคชี้ที่ตัวเลข 2 หรือ 4 มดดำจะได้เงิน 100 บาท

     ดังนั้น ผลตอบแทนของเหตุการณ์ที่มดดำได้เงิน 100 บาท จึงแทนด้วย +100

     เนื่องจาก ถ้ามดดำหมุนเสี่ยงโชคชี้ที่ตัวเลข 1, 3, 5,6,7 และ 8 มดดำไม่ต้องเสียเงิน

     ดังนั้น ผลตอบแทนของเหตุการณ์ที่มดดำไม่ต้องเสียเงิน จึงแทนด้วย 0

               ค่าคาดหมาย = (ผลตอบแทนที่ได้ × ความน่าจะเป็นของเหตุการณ์ที่ได้รับรางวัล)

                                          + (ผลตอบแทนที่เสีย × ความน่าจะเป็นของเหตุการณ์ที่ไม่ได้รับรางวัล)

                  = (100 × ¹⁄₄) + (0 × ³⁄₄) 

                  = ¹⁰⁰⁄₄

                                            = 25

     ดังนั้น ค่าคาดหมายของมดดำ เท่ากับ 25 บาท

     เนื่องจากในการซื้อตั๋วหมุนวงล้อเสี่ยงโชค 1 ใบ ราคา 50 บาท มีค่าคาดหมายที่จะได้เงิน 25 บาท     แสดงว่ามดดำเสียเปรียบอยู่ 50 – 25 = 25 บาท

     นั่นคือ ถ้ามดดำซื้อตั๋วหมุนวงล้อเสี่ยงโชคหลาย ๆ ใบ โดยเฉลี่ยแล้วแต่ละใบมดดำจะเสียเปรียบ หรือพ่อค้าได้กำไร

เมื่อน้องๆเรียนรู้เรื่อง ความน่าจะเป็นกับการตัดสินใจ จะทำให้น้องๆสามารถนำความรู้ไปใช้ในการตัดสินใจในเหตุการณ์ต่างๆ ได้เป็นอย่างดี

วิดีโอ ความน่าจะเป็นกับการตัดสินใจ