การแก้สมการกำลังสอง
การแก้สมการกำลังสอง สามารถทำได้โดยการ แยกตัวประกอบพหุนามกำลังสอง และใช้สูตร เราแก้สมการเพื่อหาคำตอบหรือหาค่าของตัวแปร
ในบทความนี้พี่จะพูดถึงสมการกำลังสองตัวแปรเดียว ซึ่งอยู่ในรูป ax² + bx + c = 0 โดยที่ a, b, c เป็นค่าคงตัว และ a ≠ 0
ตัวอย่างสมการกำลังสองตัวแปรเดียว
1.) x² + 3x +5 = 0
จะได้ว่า a = 1 , b = 3, c = 5
2.) 2x² + 5x + 1 = 0
จะได้ว่า a = 2 , b = 5 , c = 1
3.) x² + 7x = 3
เมื่อ บวกด้วย บวกเข้าด้วย -3 ทั้งสองข้างของสมการ จะได้ x² + 7x + (-3)= 3+(-3) ดังนั้น x² + 7x – 3 = 0
จะได้ว่า a = 1, b = 2, c = -3
การแก้สมการกำลังสองโดยการแยกตัวประกอบ
สมมติว่าแยกตัวประกอบพหุนามได้เป็น (x + d)(x + e) = 0 เราสามารถสรุปได้ว่า x + d = 0 หรือ x + e = 0 โดยที่ d และ e เป็นค่าคงตัว
สมการกำลังสองจะมีจำนวนคำตอบได้ไม่เกิน 2 คำตอบ
เช่น
(x – 5)(x + 2) = 0 ดังนั้น x -5 = 0 ⇒ x = 5 หรือ x +2 = 0 ⇒ x = -2
(2x + 3)(3x + 6) = 0 ดังนั้น 2x +3 = 0 ⇒ x = หรือ x + 2 = 0 ⇒ x = -2
ทำไมถึงรู้ว่า ในวงเล็บเท่ากับ 0 ???
ลองพิจารณา (x – 5)(x + 2) = 0
ให้ a แทน x – 5
b แทน x + 2
จะได้ว่า ab = 0 เราลองคิดง่ายๆเลย จำนวนที่คูณกันแล้วจะได้ 0 ต้องมีตัวใดตัวหนึ่งเป็น 0 แสดงว่าไม่ a ก็ b ต้องเท่ากับ 0 หรืออาจจะเป็น 0 ทั้ง a และ b
ดังนั้นเราจึงได้ว่า ab = 0 แล้ว a = 0 หรือ b = 0
นั่นคือ x – 5 = 0 หรือ x + 2 = 0
การใช้สูตร การแก้สมการกำลังสอง
ให้ ax² + bx + c = 0 โดยที่ a, b, c เป็นค่าคงตัว และ a ≠ 0
สูตรที่เราจะใช้ในการแก้สมการกำลังคือ
ข้อดีของการใช้สูตรเราสามารถรู้ได้ว่า สมการนั้นมีจำนวนคำตอบเท่าใด โดยพิจารณา
> 0 แสดงว่าสมการมี 2 คำตอบ
= 0 แสดงว่าสมการมี 1 คำตอบ
< 0 แสดงว่าไม่มีคำตอบของสมการที่เป็นจำนวนจริง (หมายความว่ามีคำตอบแต่คำตอบนั้นไม่ใช่จำนวนจริง)
เราสามารถตรวจคำตอบของสมการได้ โดยการนำคำตอบที่ได้ แทนค่าลงไปใน x ถ้าสมการเป็นจริงแสดงว่า “คำตอบถูกต้อง”
ตัวอย่าง
x² + 3x +5 = 0
เนื่องจาก = -11 ซึ่งน้อยกว่า 0 ดังนั้น x ไม่มีคำตอบในจำนวนจริง
ตัวอย่าง
1.) x² + 3x -10 = 0
วิธีทำ 
2.) 10x² – 7x -12 = 0
วิธีทำ 
3.) x² + 3x +3 = 0
วิธีทำ

4.) (x -2)² = 0
วิธีทำ

5.) พิจารณาสมการต่อไปนี้ว่ามีกี่คำตอบ
5.1) x² + 9x + 1 = 0
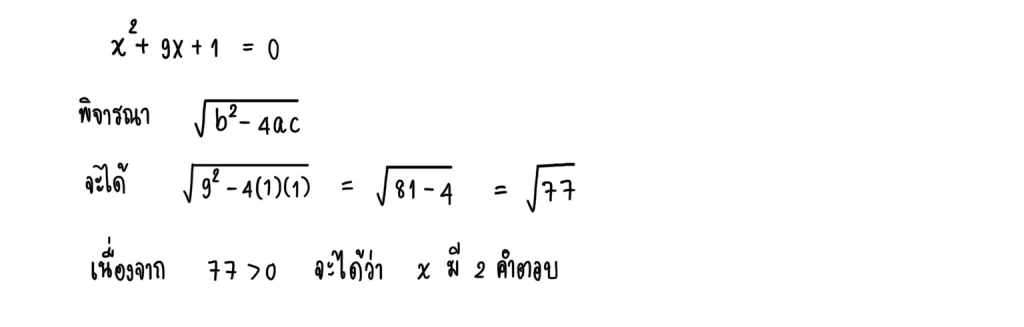
5.2) x² + 10x + 25 = 0
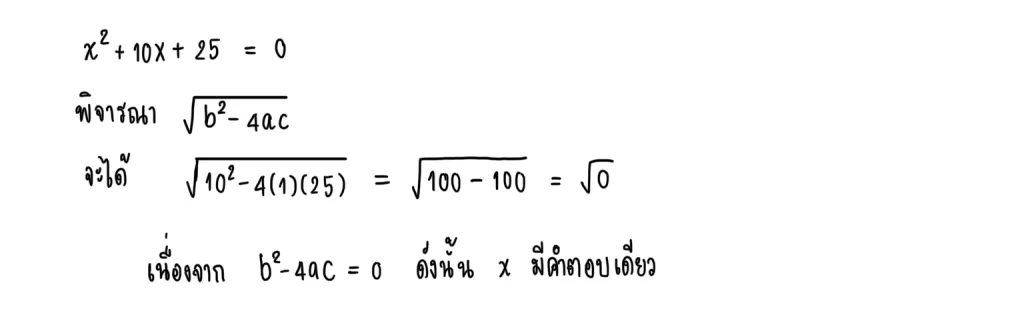
5.3) x² + 2x + 10 = 0
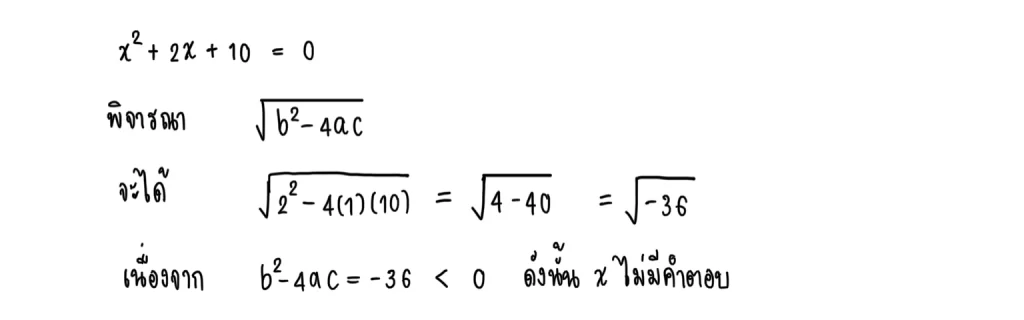
วีดิโอการแก้สมการกำลังสอง