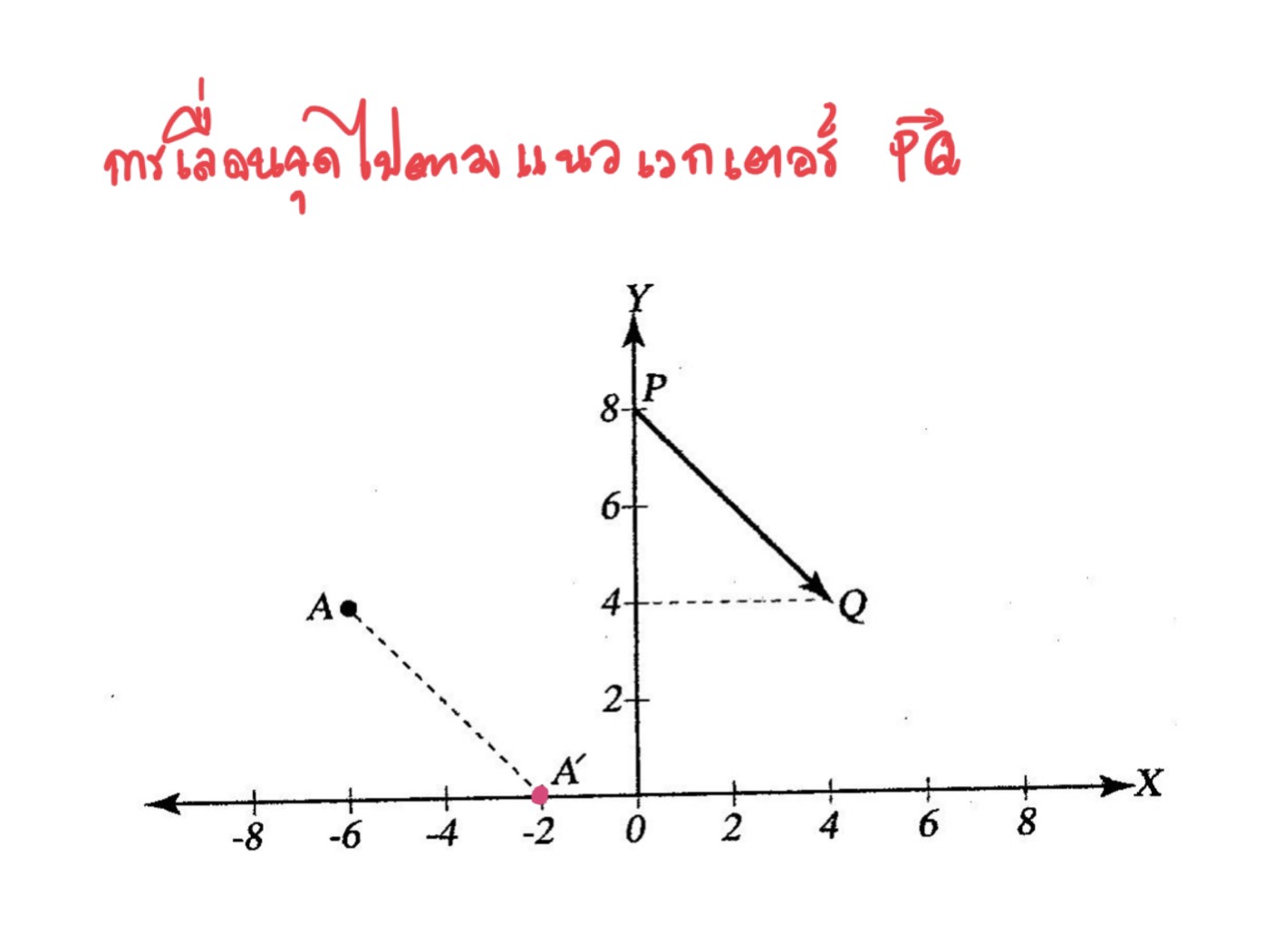
การเลื่อนขนาน

สำหรับการแปลงทางเรขาคณิตในบทนี้จะกล่าวถึงการแปลงที่จะได้ภาพที่มีรูปร่างเหมือนกันและขนาดเดียวกันกับรูปต้นแบบเสมอ โดยใช้การเลื่อนขนาน

tucksaga

การเลื่อนขนาน, คณิตศาสตร์, คณิตศาสตร์ ม.2, ม.2, เลื่อนขนาน ม.2

Add LINE friends for one click to find article.

การแปลงทางเรขาคณิตในบทความนีจะกล่าวถึงการเคลื่อนไหวของรูปเรขาคณิตแบบการเลื่อนขนาน (Translation) โดยมีรูปเรขาคณิตทั้ง จุด เส้น และรูปร่าง ซึ่งมักจะพบบ่อยในชีวิตประจำวัน

รูปแบบการเลื่อนขนาน

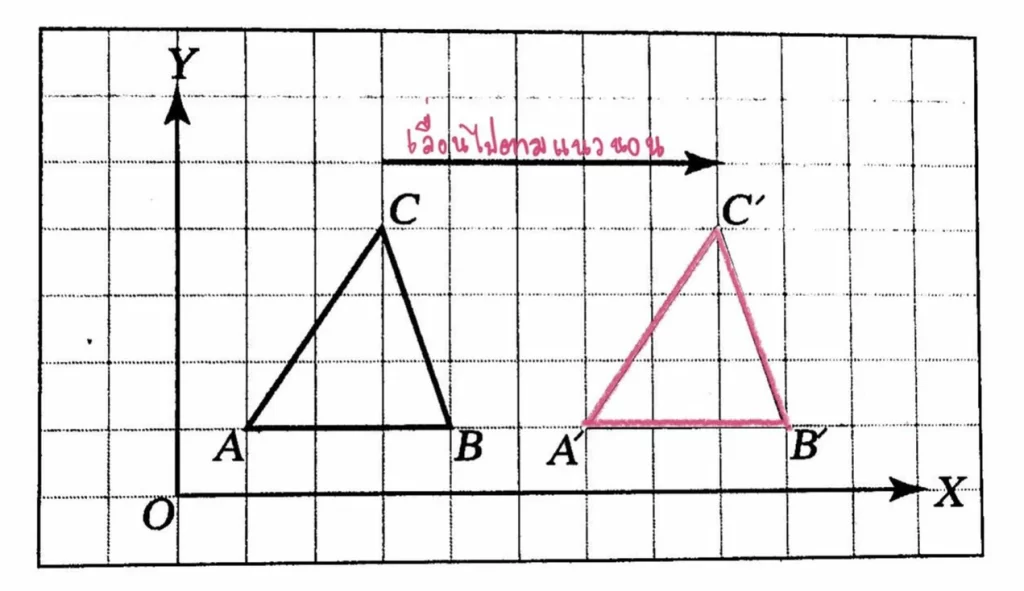
พิจารณารูป สามเหลี่ยม ABC บนระนาบจำนวนและ สามเหลี่ยมA’B’C ‘เป็นภาพของ สามเหลี่ยม ABC ที่เกิดการเลื่อนไปตามแนวนอน

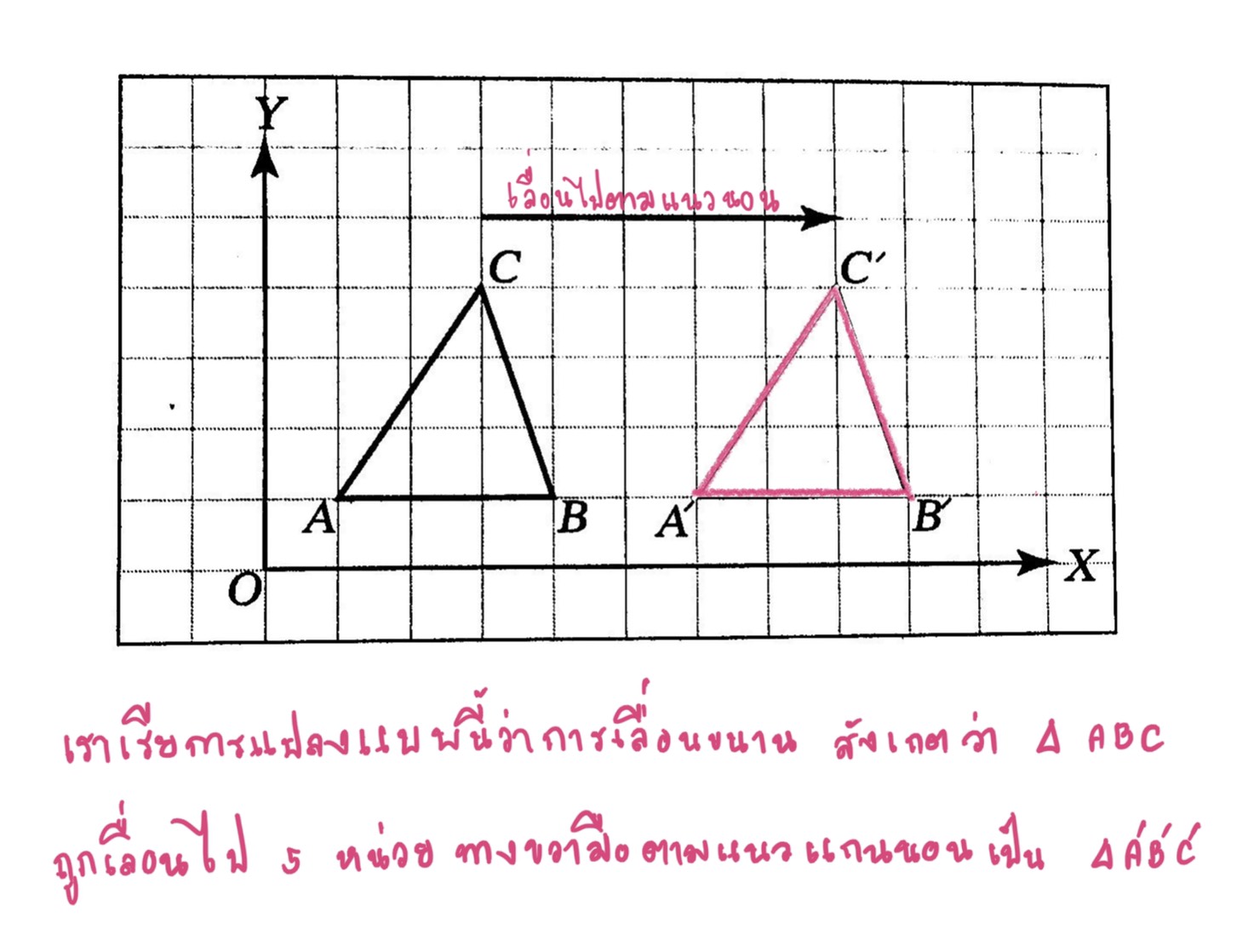
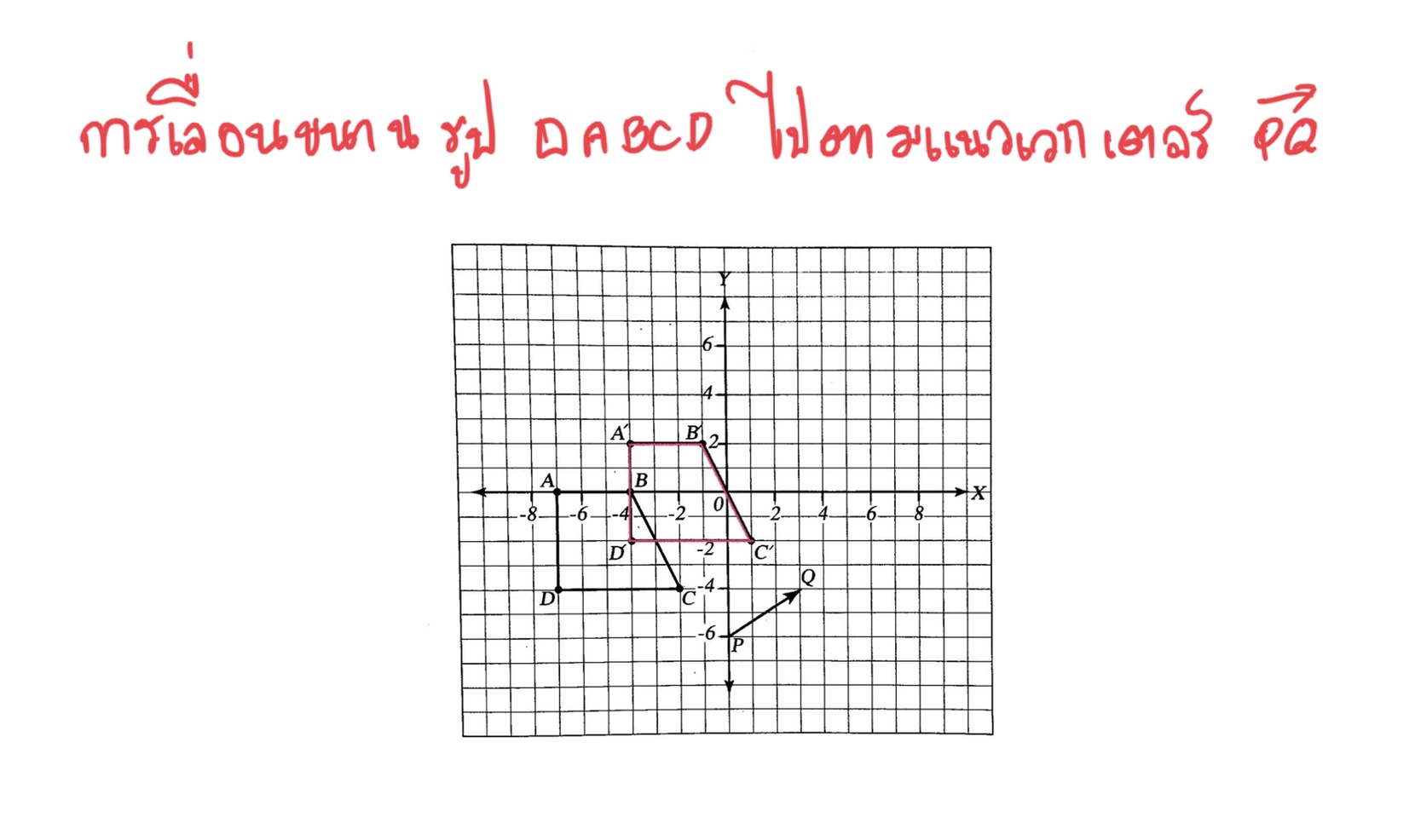
และรูปต่อไปเป็นการเลื่อนขนานไป 4 หน่วย ขึ้นไปตามแนวแกนตั้ง

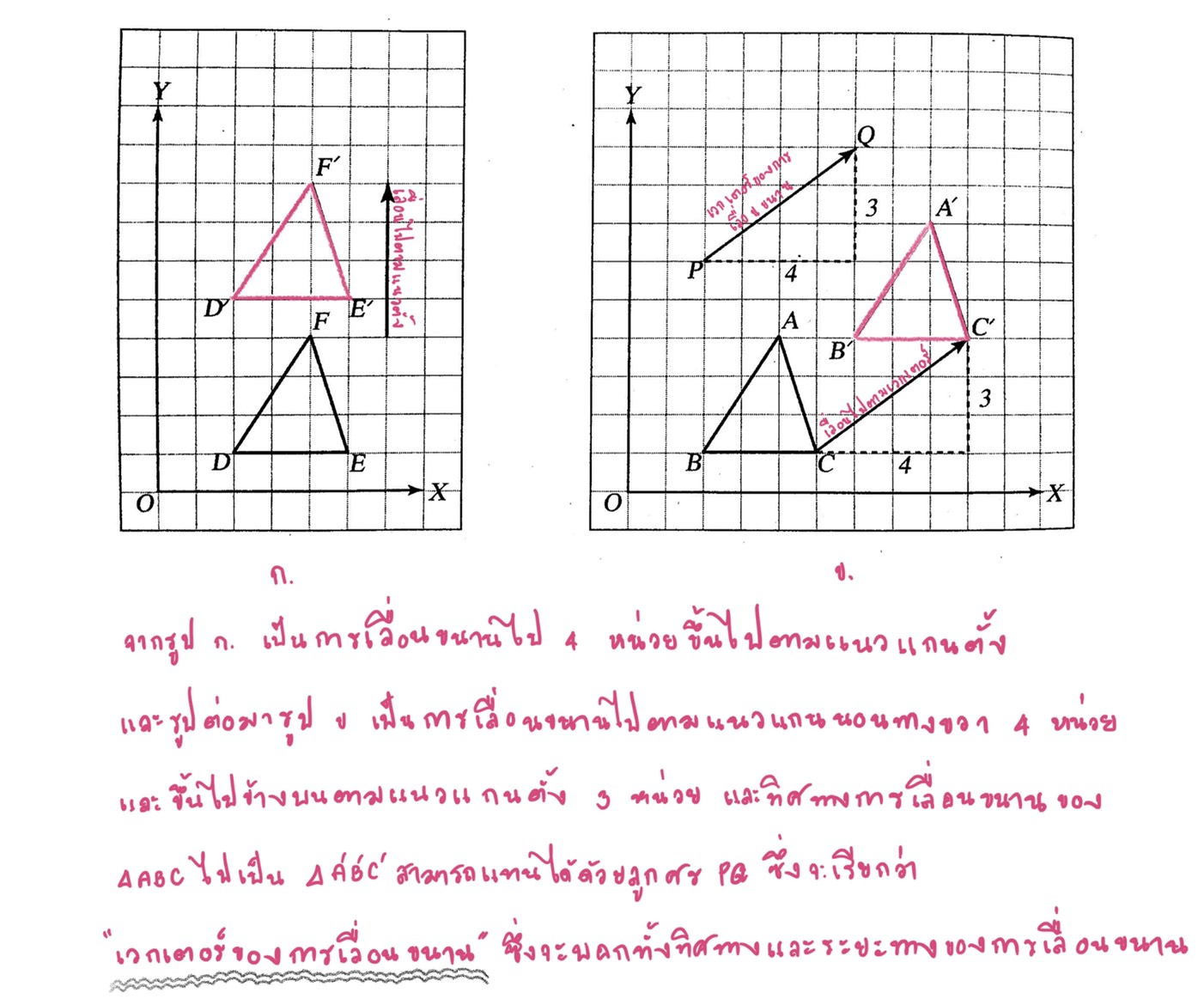
สมบัติของการเลื่อนขนาน

สามารถเลื่อนรูปต้นแบบทับภาพที่ได้จากการเลื่อนขนานได้สนิทโดยไม่ต้องพลิกรูปสมบัติของการเลื่อนขนานหรือกล่าวได้ว่ารูปต้นแบบและภาพที่ได้จากการเลื่อนขนานจะเท่ากันทุกประการ
ส่วนของเส้นตรงบนรูปต้นแบบและภาพที่ได้จากการเลื่อนขนานของส่วนของเส้นตรงนั้นจะขนานกัน

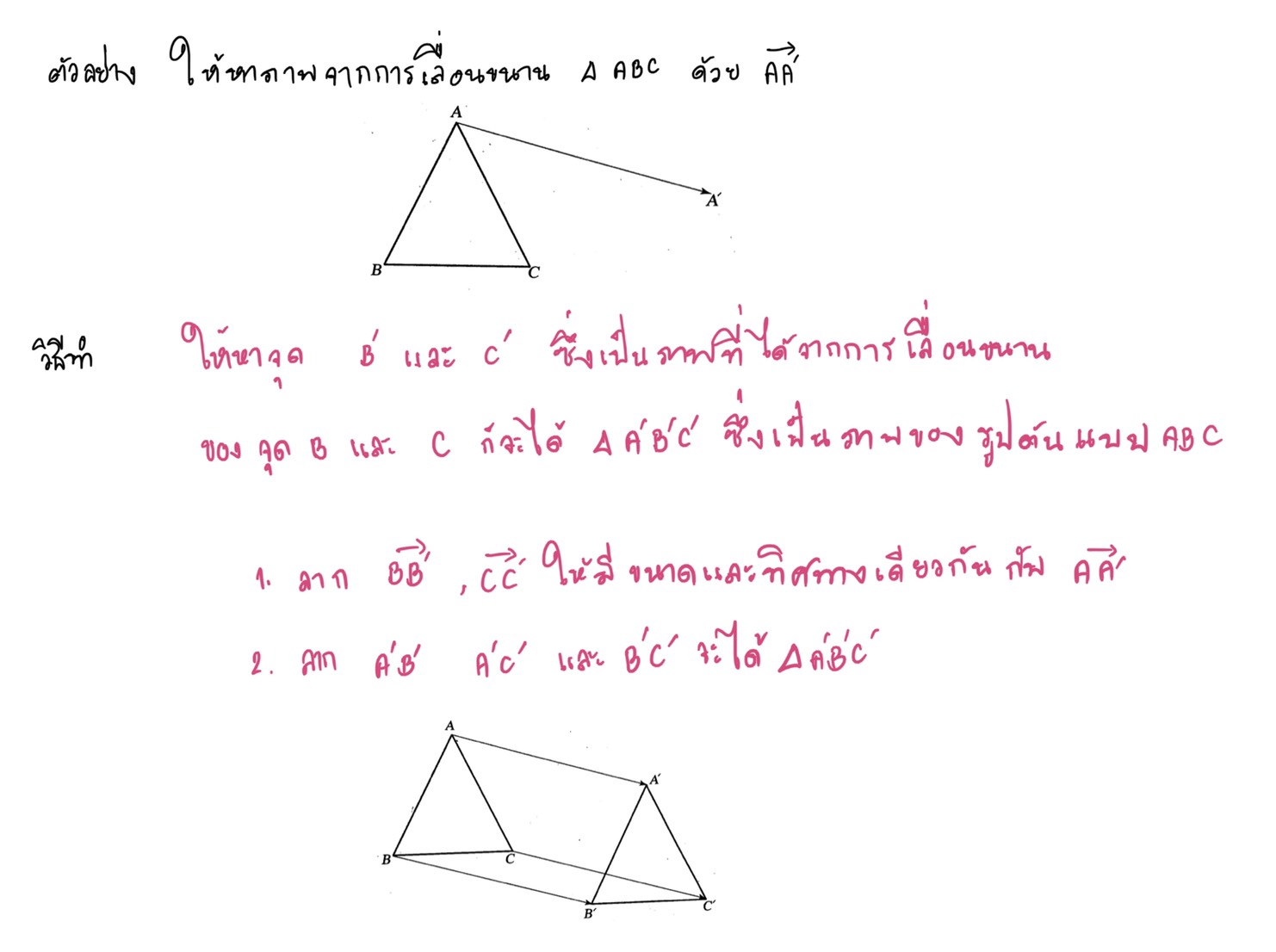
จากตัวอย่างจะเห็นว่าเมื่อกำหนดรูปต้นแบบและเวกเตอร์ของการเลื่อนขนานมาให้เราสามารถหาภาพที่ได้จากการเลื่อนขนานได้และในทางกลับกันถ้ากำหนดรูปต้นแบบและภาพที่ได้จากการเลื่อนขนานมาให้ต้องสามารถหาเวกเตอร์ของการเลื่อนขนานได้เช่น สามเหลี่ยมABC เลื่อนขนานไปเป็น A’B’C’ ดังรูป

คลิปตัวอย่างเรื่องการเลื่อนขนาน

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

โวหารภาพพจน์ กลวิธีการสร้างจินตภาพที่ลึกซึ้งและสวยงาม

การสร้างจินตภาพอย่างการใช้ โวหารภาพพจน์ เป็นกลวิธีในการใช้ภาษาอีกอย่างหนึ่ง เลือกใช้ถ้อยคำเพื่อให้ผู้อ่านเห็นภาพ หรืออาจเรียกว่าเป็นการแทนภาพนั่นเอง น้อง ๆ คงจะพบเรื่องของโวหารภาพพจน์ได้บ่อย ๆ เวลาเรียนเรื่องวรรณคดี บทเรียนในวันนี้เลยจะพาไปทำความรู้จักกับภาพพจน์ต่าง ๆ ให้มากขึ้นว่ามีอะไรบ้าง ถ้าพร้อมแล้วไปดูพร้อมกันเลยค่ะ ความหมายของภาพพจน์ ภาพพจน์ คือถ้อยคำที่เป็นสำนวนโวหารทำให้นึกเห็นภาพ ถ้อยคำที่เรียบเรียงอย่างมีชั้นเชิงเป็นโวหาร มีเจตนาให้มีประสิทธิผลต่อความคิด เป็นกลวิธีทางภาษาที่มุ่งให้เกิดความรู้ความเข้าใจจินตนาการ เน้นให้เกิดอรรถรสและสุนทรีย์ในการสื่อสารที่ลึกซึ้งกว่าการบอกเล่าแบบตรงไปตรงมา

ศิลาจารึก วรรณคดีเชิงประวัติศาสตร์ที่สำคัญของคนไทย

ศิลาจารึก เป็นวรรณคดีเชิงประวัติศาสตร์ บทเรียนภาษาไทยในวันนี้จะพาน้อง ๆ ย้อนอดีตไปในสมัยสุโขทัยเพื่อเรียนรู้ประวัติความเป็นมาของศิลาจารึก ที่เป็นการบันทึกเรื่องราวต่าง ๆ บนแผ่นดิน ถ้าอยากรู้แล้วว่าแผ่นหินที่ว่านี่มีประวัติความเป็นมาอย่างไร ก็ไปเรียนรู้พร้อม ๆ กันเลยค่ะ ศิลาจารึกหลักที่ 1 ประวัติความเป็นมา ศิลาจารึกหลักที่ 1 จารึกโดยพ่อขุนรามคำแหง ใช้อักษรไทย สุโขทัย หรือ ลายสือไทย

การใช้คำสันธาน (Conjunctions) เช่น and/ but/ or/ before/ after and etc.

สวัสดีค่ะนักเรียนชั้นม.2 ที่รักทุกคนวันนี้เราจะไปเรียนรู้กันเรื่อง “การใช้คำสันธาน (Conjunctions) เช่น and/ but/ or/ before/ after and etc.” กันนะคะ ถ้าพร้อมแล้วก็ไปลุยกันโลด คำสันธาน(Conjunctions)คืออะไร คำสันธาน (Conjunctions) คือ คำที่ใช้เชื่อมระหว่างประโยคต่อประโยค คำต่อคำ หรือระหว่างกริยาต่อกริยา และอื่นๆ เช่น and/

Signal Words ที่จะช่วยให้อ่านและเขียนภาษาอังกฤษได้ดียิ่งขึ้น

สวัสดีน้องๆ ม. 3 ทุกคนนะครับ วันนี้เราจะมาทำความรู้จักกับ Signal Words ในภาษาอังกฤษกันครับ ถ้าพร้อมแล้วไปดูกันเลย

กาพย์พระไชยสุริยา ศึกษาตัวบทที่น่าสนใจและคุณค่าที่อยู่ในเรื่อง

กาพย์พระไชยสุริยา กาพย์พระไชยสุริยาเป็นวรรณคดีที่ทรงคุณค่า เป็นแบบเรียนภาษาไทยที่มีมาแต่โบราณ นอกจากนี้ยังสอนเรื่องราวต่าง ๆ อีกมากมาก หลังจากที่ได้เรียนรู้เกี่ยวกับประวัติความเป็นมา ลักษณะคำประพันธ์และเนื้อเรื่องกันไปแล้ว เรื่องต่อไปที่น้อง ๆ จะได้เรียนรู้ก็คือตัวบทเด่น ๆ ที่น่าสนใจในเรื่องกาพย์พระไชยสุริยาค่ะ เรามาดูกันดีกว่านะคะว่าในกาพย์พระไชยสุริยาจะมีตัวบทไหนเด่น ๆ และมีคุณค่าอย่างไรบ้าง ตัวบทที่น่าสนใจในกาพย์พระไชยสุริยา ลักษณะคำประพันธ์ : กาพย์สุรางคนางค์ 28

การใช้ Verb Be

สวัสดีค่ะนักเรียนชั้นม.1 ที่รักทุกคน วันนี้เราจะไปเรียนรู้เรื่อง การใช้ Verb Be กันนะคะ พร้อมแล้วก็ไปลุยกันเลยจ้า Let’s go! ความหมาย Verb be ในที่นี้จะแปลว่า Verb to be นะคะ แปลว่า เป็น อยู่ คือ ซึ่งหลัง verb to

การเลื่อนขนาน

สารบัญ