การประยุกต์ของการแปลงทางเรขาคณิตเป็นการเปลี่ยนตำแหน่งของรูปเรขาคณิต โดยลักษณะและขนาดของรูปยังคงเดิม โดยใช้การสะท้อนเช่นเดียวกัยการที่เราไปยืนหน้ากระจก
ความหมายของการสะท้อน
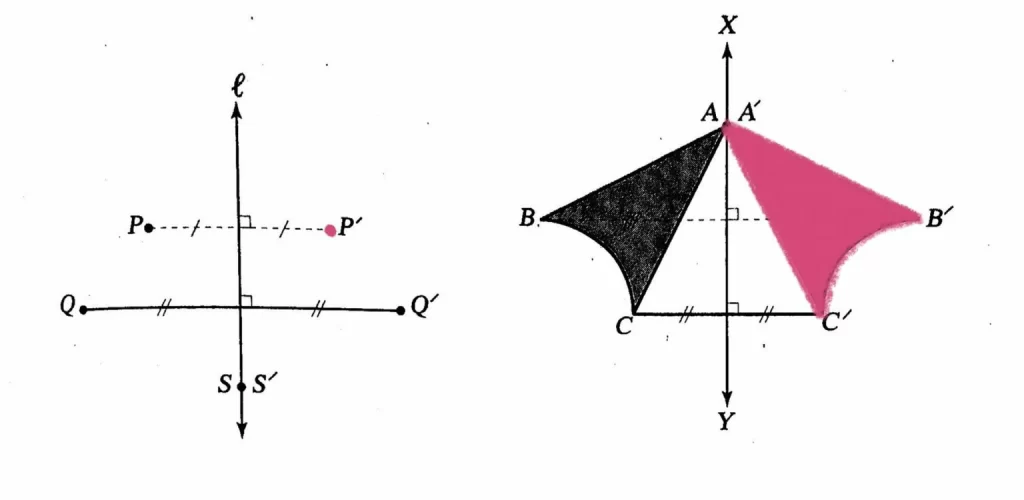
การสะท้อนบนระนาบเป็นการแปลงทางเรขาคณิตที่มีเส้นตรง l เป็นเส้นสะท้อนแต่ละจุด P บนระนาบจะมีจุด P´ เป็นภาพที่ได้จากการสะท้อนจุด P โดยที่
- ถ้าจุด P ไม่อยู่บนเส้นตรง l แล้วเส้นตรง l จะแบ่งครึ่งและตั้งฉากกับส่วนของเส้นตรง PP´
- ถ้าจุด P อยู่บนเส้นตรง l แล้วจุด P และ P´ เป็นจุดเดียวกัน
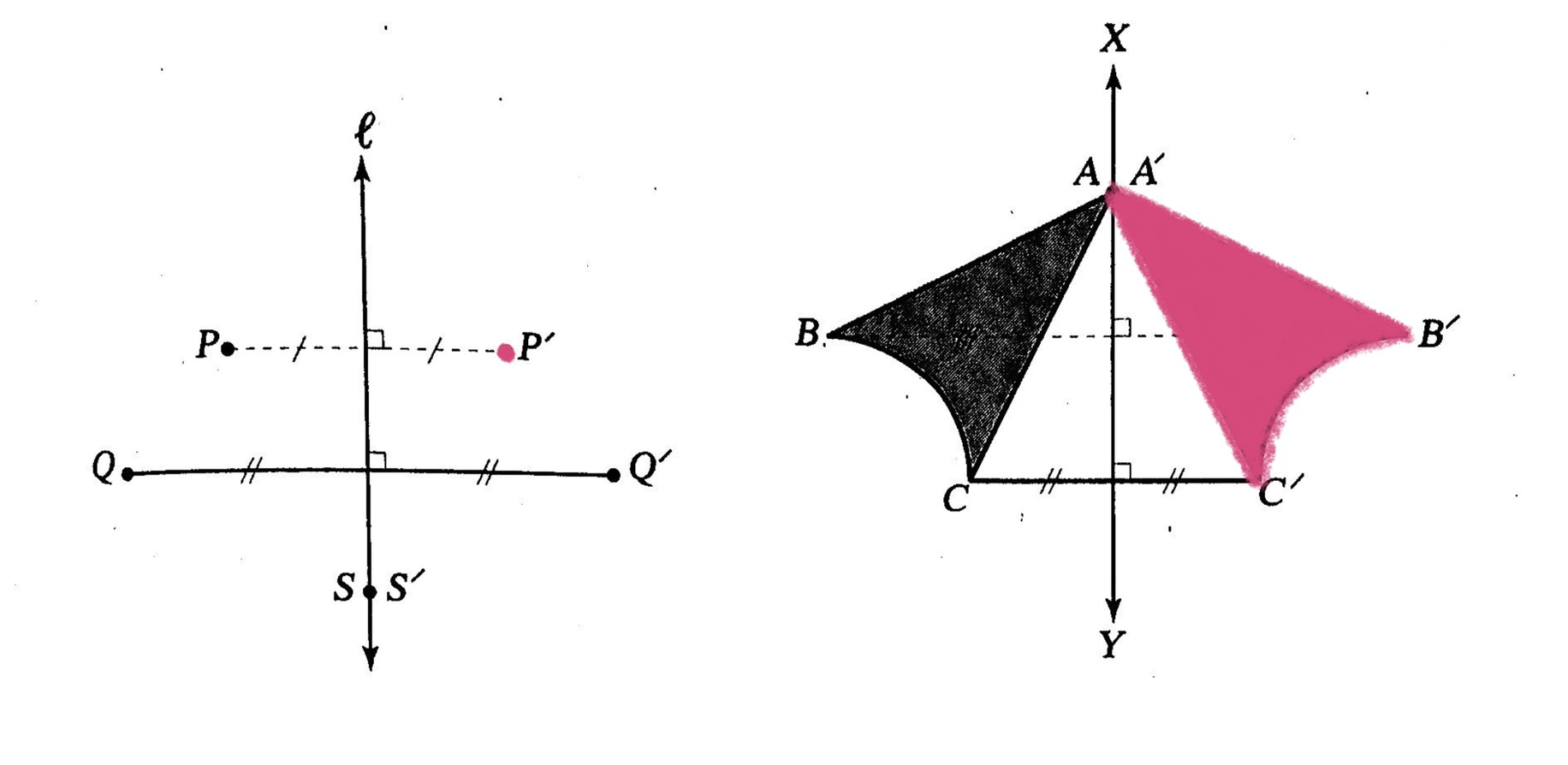
สมบัติการสะท้อน
- สามารถเลื่อนรูปต้นแบบทับภาพที่ได้จากการสะท้อนได้สนิทโดยต้องพลิกรูปหรือกล่าวว่ารูปต้นแบบและภาพที่ได้จากการสะท้อนเท่ากันทุกประการ
- ส่วนของเส้นตรงบนรูปต้นแบบและภาพที่ได้จากการสะท้อนของส่วนของเส้นตรงนั้นไม่จำเป็นต้องขนานกันทุกคู่
- ส่วนของเส้นตรงที่เชื่อมจุดแต่ละจุดบนรูปต้นแบบกับจุดที่สมนัยกันบนภาพที่ได้จากการสะท้อนจะขนานกันและไม่จำเป็นต้องยาวเท่ากัน
การหาภาพที่ได้จากการสะท้อนเมื่อกำหนดรูปต้นแบบและเส้นสะท้อนมาให้
กำหนดให้ รูปสี่เหลี่ยม ABCD เป็นรูปต้นแบบและ เส้นตรงXY เป็นเส้นสะท้อนจงหาภาพที่ได้จากการสะท้อนของรูปสี่เหลี่ยม ABCD
วิธีสร้าง
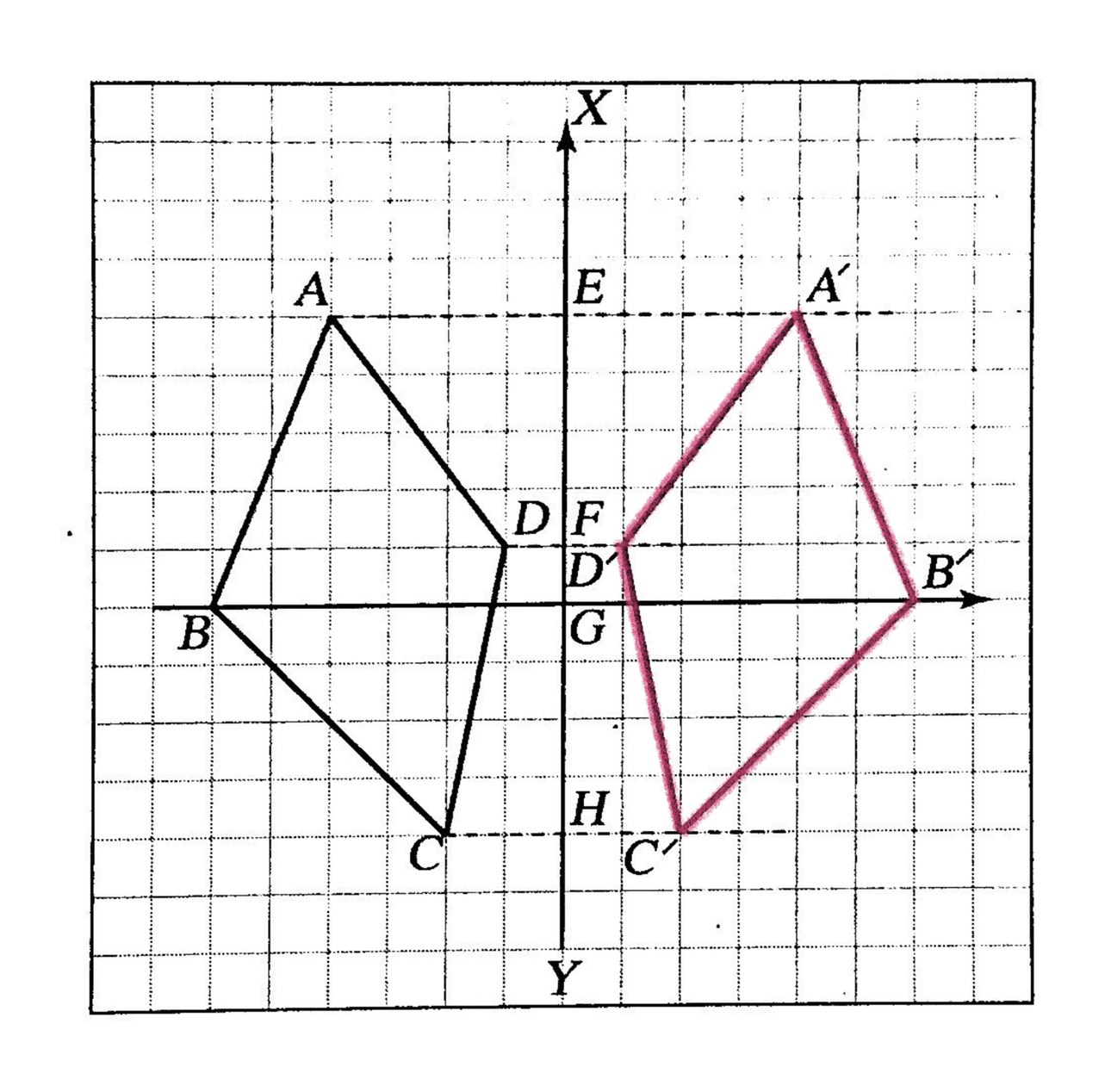

การหาเส้นสะท้อนเมื่อกำหนดรูปต้นแบบและภาพที่ได้จากการสะท้อน
กำหนดให้ สามเหลี่ยม A’B’C’ เป็นภาพที่ได้จากการสะท้อน สามเหลี่ยมABC ดังรูป
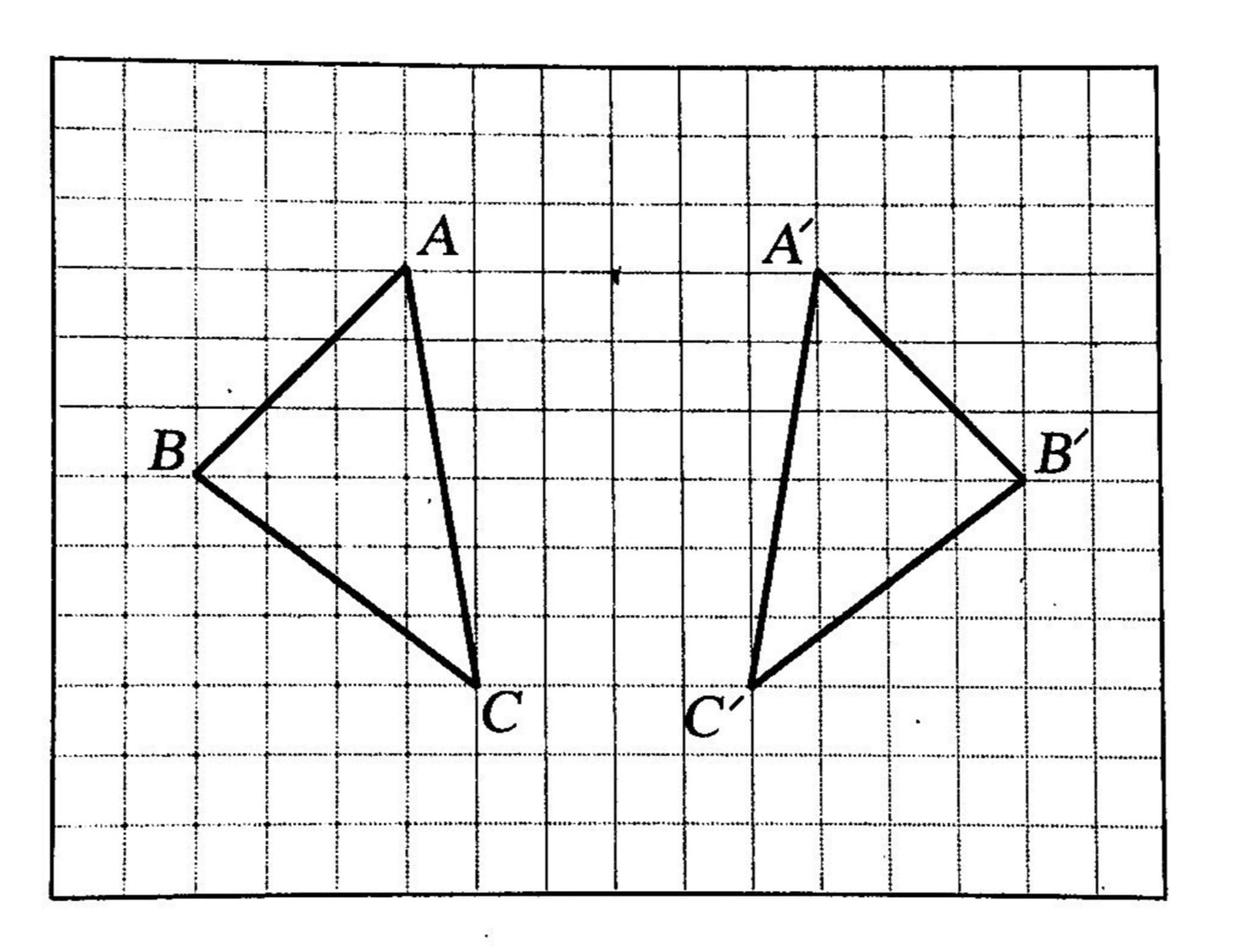
แนวคิด การหาเส้นสะท้อนที่มีสามเหลี่ยมA’B’C’ เป็นภาพที่ได้จากการสะท้อนทำได้โดยลากส่วนของเส้นตรงเชื่อมระหว่างจุดที่สมนัยกับคู่ใดคู่หนึ่งของ สามเหลี่ยมABC และ สามเหลี่ยมA’B’C เช่น อาจจะลาก AA’ , BB’ หรือ CC’ ก็ได้
แล้วลากเส้นแบ่งครึ่งและตั้งฉากกับ AA’ จะได้เส้นสะท้อนตามต้องการดังรูป
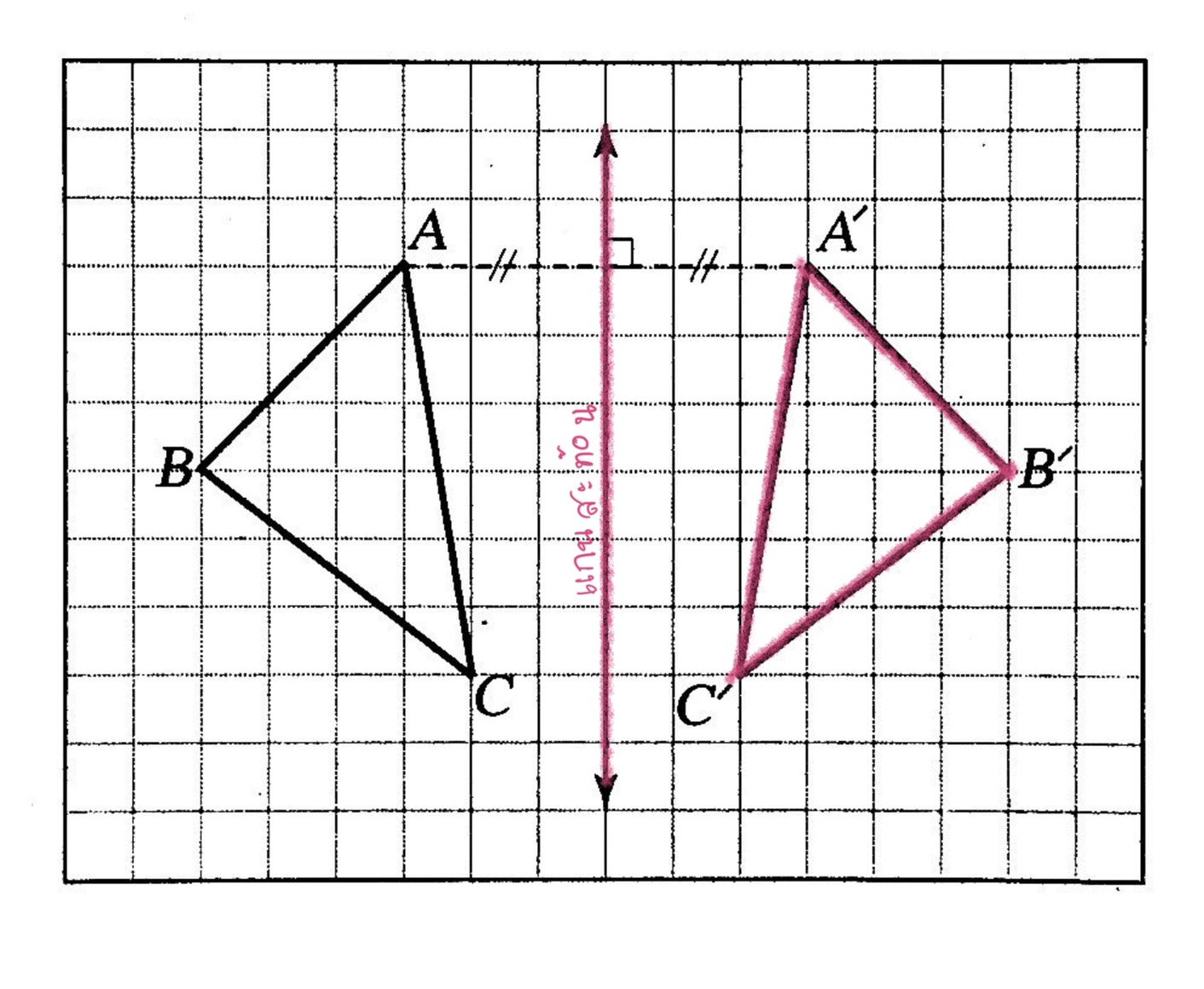
การหาภาพจากการสะท้อนที่แกน X และแกน Y
กำหนดให้ สามเหลี่ยมABC และต้องการหาภาพจากการสะท้อนที่แกน X และสะท้อนที่แกน Y
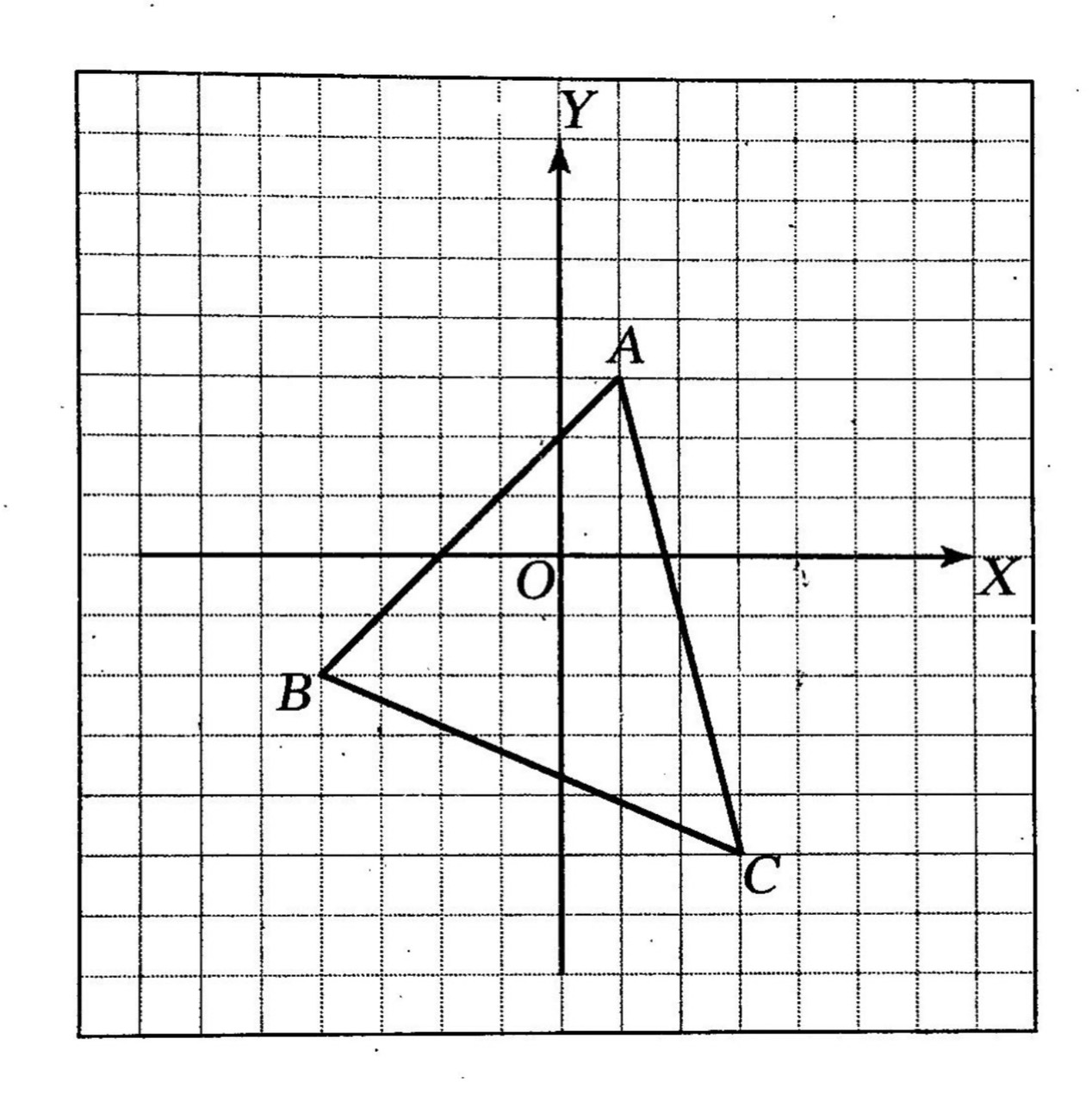
แนวคิด การหาภาพจากการสะท้อนที่แกน X
จากรูป สามเหลี่ยมABC มีแกน X เป็นเส้นสะท้อนจะมีจุด A’, B’ และ C’ เป็นภาพที่ได้จากการสะท้อนจุด A, B และ C ตามลำดับ ซึ่งพิกัดของจุดแต่ละคู่ที่สมนัยกันจะมีพิกัดที่หนึ่งเป็นจำนวนเดียวกันเพราะอยู่ด้านเดียวกันและห่างจากแกน Y เป็นระยะที่เท่ากันและมีพิกัดที่สองเป็นจำนวนตรงข้ามกันเพราะอยู่คนละด้านของแกน X เป็นระยะทางที่เท่ากันและภาพที่ได้มีลักษณะดังรูป
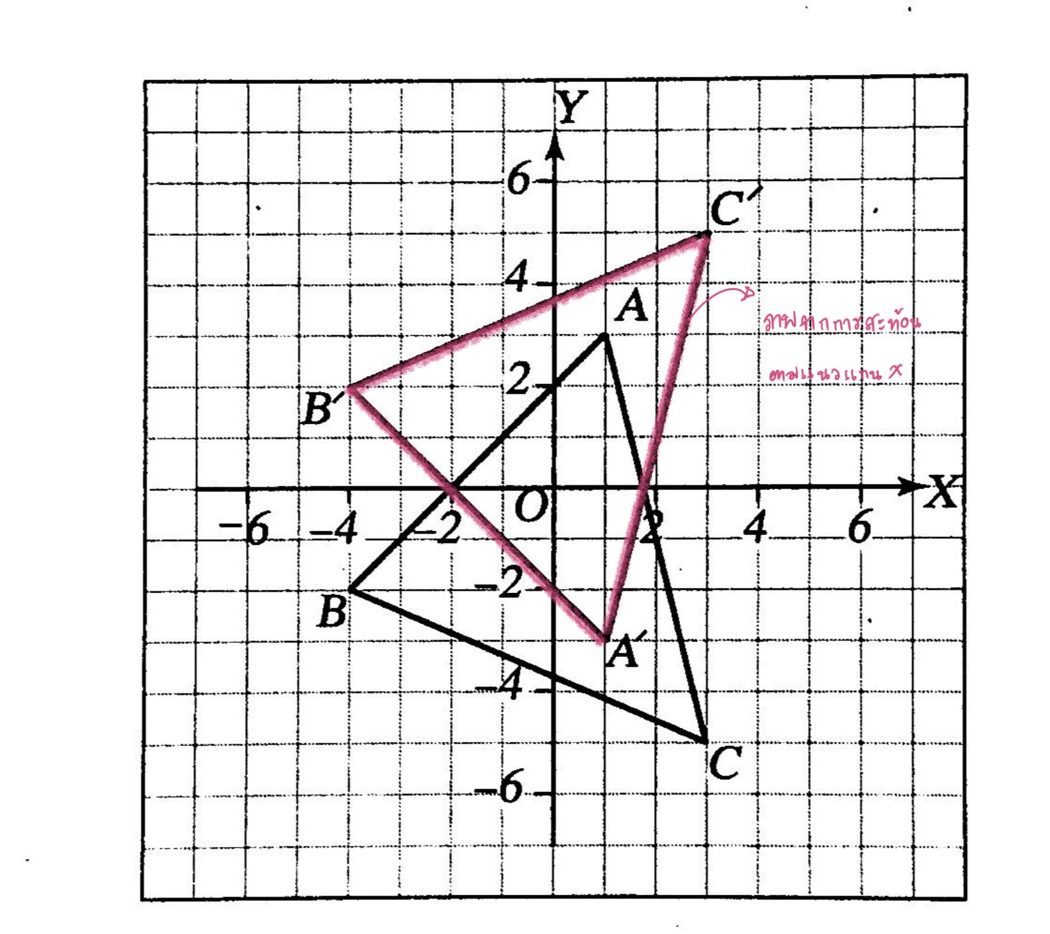
การหาพิกัดของจุด A’ , B’ และ C’ หาได้โดยพิจารณาพิกัดของ A, B, C
คือ A (1, 3) → A ‘(1, -3)
B (-4, -2) → B’ (-4. 2)
C (3. -5) → C ‘(3.5)
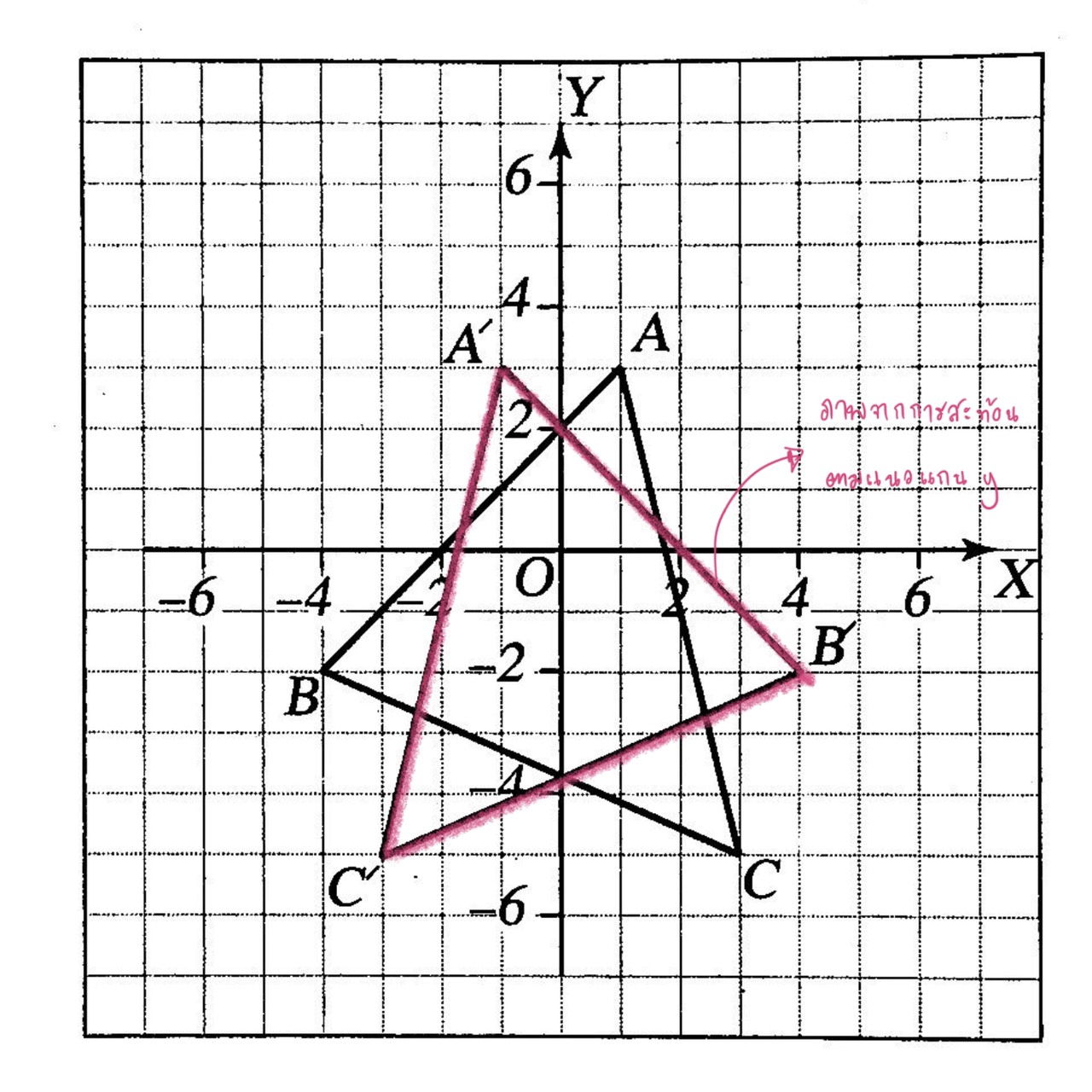
การหาภาพจากการสะท้อนที่แกน Y
ทำได้โดยการพิจารณาพิกัดของ A’ , B’ และ C’ จากพิกัดของ A, B และ C ดังนี้
A (1, 3) → A ‘(-1, 3)
B (-4, -2) → B’ (4. -2)
C (3. -5) → C'(-3, -5)
การหาภาพที่สะท้อนกับเส้นสะท้อนที่ขนานกับแกน X หรือขนานกับแกน Y
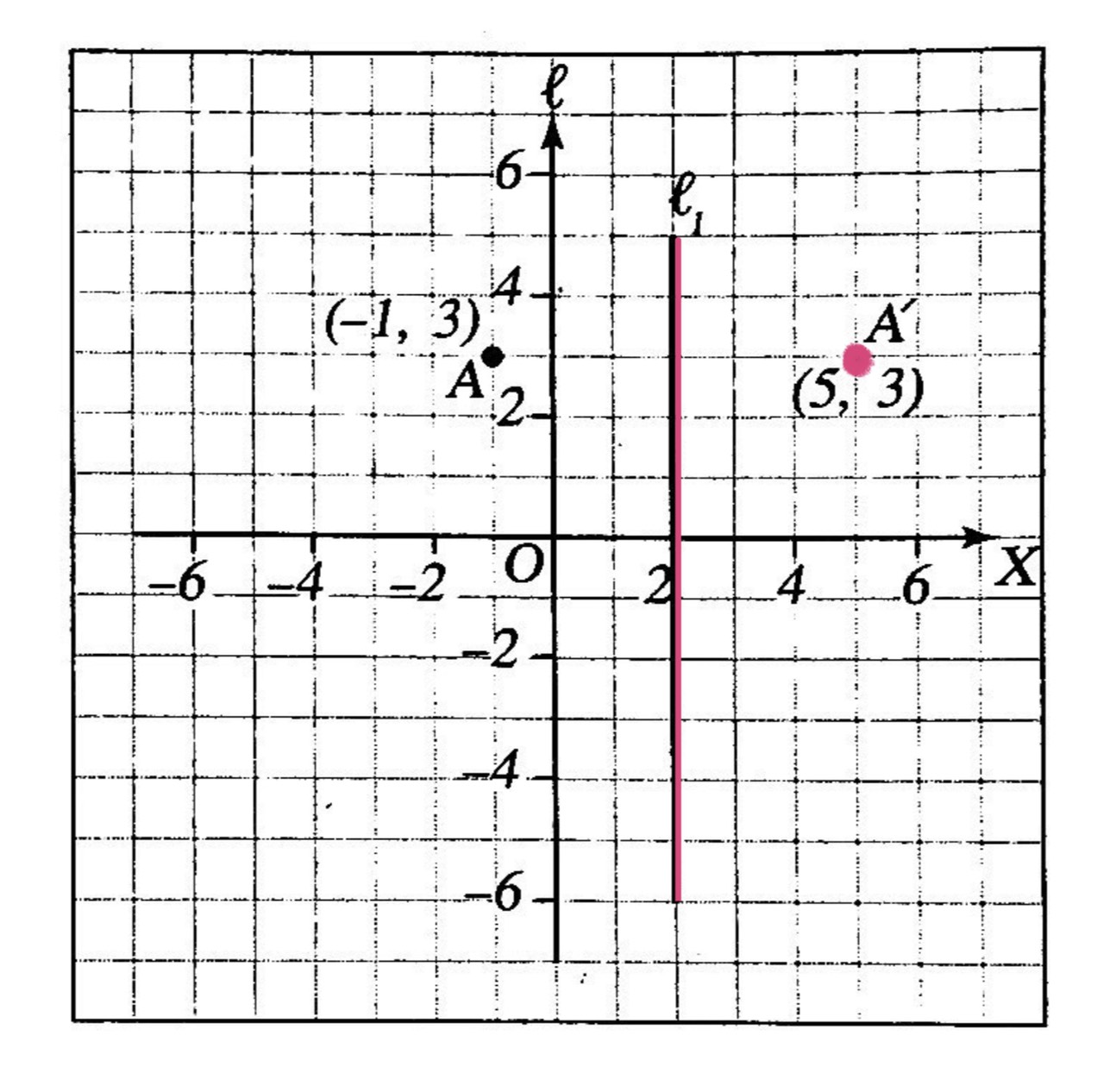
ถ้าเส้นสะท้อนขนานกับแกน X หรือแกน Y ให้นับช่องตารางหาระยะระหว่างจุดที่กำหนดให้กับเส้นสะท้อนซึ่งภาพของจุดนั้นจะอยู่ห่างจากเส้นสะท้อนเป็นระยะที่เท่ากันกับระยะที่นับได้เมื่อได้ภาพของจุดนั้นแล้วจึงหาพิกัด
ตัวอย่างเช่น ภาพของ A ที่สะท้อนที่เส้นตรง l เป็นภาพที่ A’
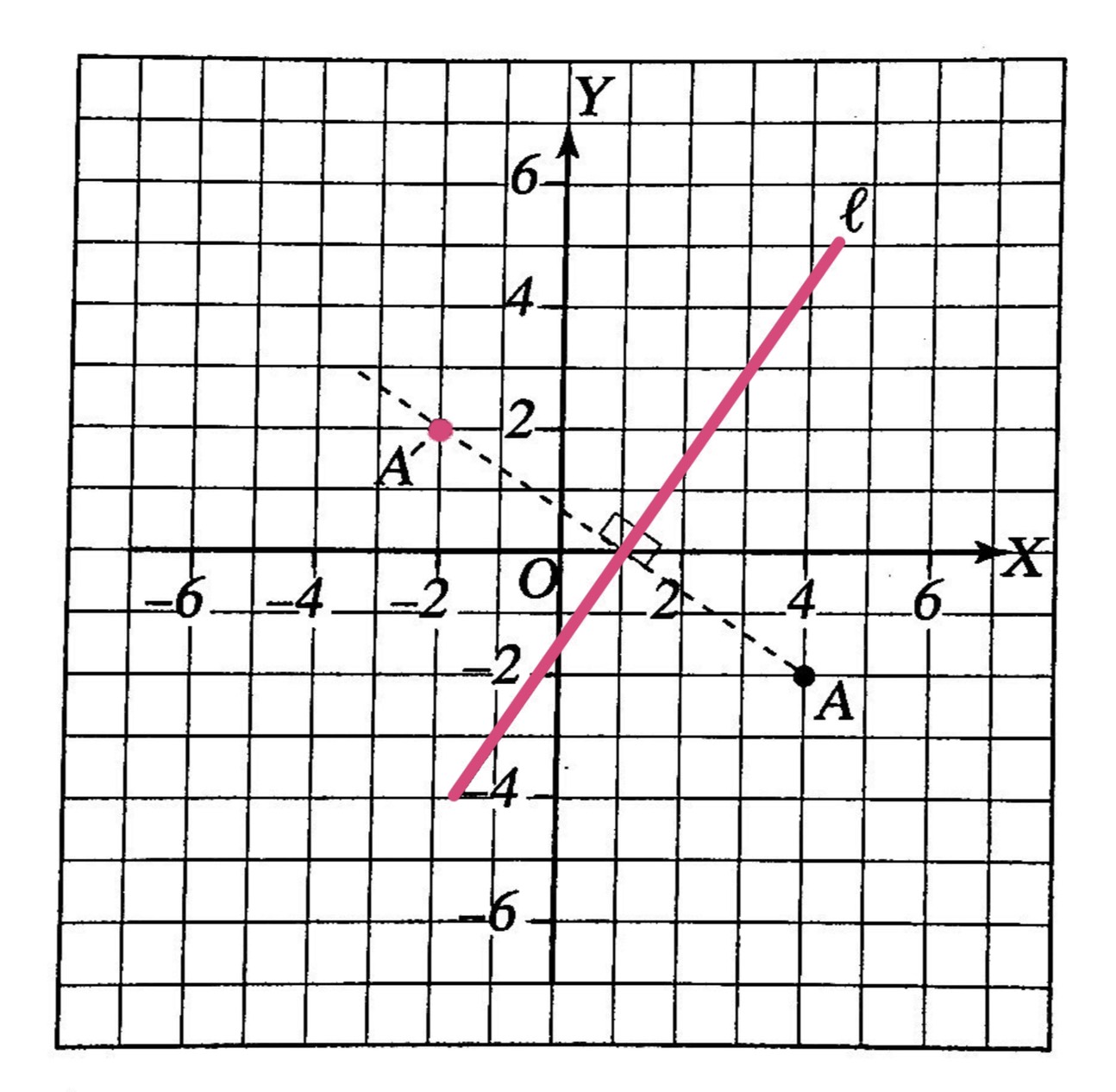
การหาภาพที่สะท้อนกับเส้นสะท้อนที่ไม่ขนานกับแกน X และไม่ขนานกับแกน Y
ในกรณีที่เส้นสะท้อนไม่ขนานกับแกน X และแกน Y แต่เป็นเส้นในแนวทแยงให้ลากเส้นตรงผ่านจุดที่กำหนดให้และตั้งฉากกับเส้นสะท้อนภาพของจุดที่กำหนดให้จะอยู่บนเส้นตั้งฉากที่สร้างขึ้นและอยู่ห่างจากเส้นสะท้อนเป็นระยะเท่ากับจุดที่กำหนดให้อยู่ห่างจากเส้นสะท้อนเมื่อได้ภาพของจุดนั้นแล้วจึงหาพิกัด
ตัวอย่างเช่นภาพของจุด A(4, 2) สะท้อนกับเส้นตรง l ได้ภาพที่ A’ ดังรูป