กราฟที่ได้จากจุดที่เรียงอยู่ในแนวเส้นตรงเดียวกันความสัมพันธ์ของจำนวนเต็มทั้งสองจึงเป็นความสัมพันธ์เชิงเส้นและแสดงเป็น กราฟของสมการเชิงเส้นสองตัวแปร ซึ่งการหาจุดตัดของแกน x และแกน yจะช่วยในการเขียนกราฟได้ง่ายขึ้น
กราฟของสมการเชิงเส้นสองตัวแปร (จุดตัดแกน x และจุดตัดแกน y)
เราสามารถลากเส้นตรงผ่านจุดสองจุดใด ๆ ที่แตกต่างกันได้เพียงเส้นเดียวเท่านั้น ดังนั้นเพื่อความสะดวกรวดเร็วในการเขียนกราฟเส้นตรง เราจึงเลือกคู่อันดับสองคู่อันดับที่สอดคล้องกับสมการเชิงเส้นสองตัวแปรที่กำหนดให้ และเขียนกราฟของคู่อันดับทั้งสองบนระนาบแล้วลากเส้นตรงผ่านจุดสองจุดนั้น เส้นตรงนั้นจะเป็นกราฟของสมการเชิงเส้นสองตัวแปรที่กำหนดให้
จุดตัดบนกราฟสมการเชิงเส้นสองตัวแปร
กราฟแสดงความสัมพันธ์ของปริมาณสองปริมาณในวิชาพีชคณิตนั้น จะมีแกนนอนหรือเรียกว่าแกน x และแกนตั้งหรือเรียกว่าแกน y บริเวณที่เส้นกราฟซึ่งแสดงข้อมูลตัดผ่านแกนจะเรียกว่า จุดตัด
จุดตัดแกน x และจุดตัดแกน y
หากเส้นกราฟตัดผ่านแกน y จะเรียกว่า จุดตัดแกน y และหากเส้นกราฟตัดผ่านแกน x จะเรียกว่า จุดตัดแกน x การหาจุดตัดแกน x ตามหลักพีชคณิตจะหาได้ง่ายหรือยากขึ้นอยู่กับประเภทของสมการ โดยการหาจุดตัด จะสามารถนำไปใช้ในการสร้างกราฟของสมการเชิงเส้นสองตัวแปร หรือที่เรียกกันว่ากราฟเส้นตรงได้ง่ายขึ้น
การหาคู่อันดับ
ในการหาคู่อันดับที่สอดคล้องกับสมการเชิงเส้นสองตัวแปร เพื่อความสะดวกในการคำนวณ อาจหาคู่อันดับสองคู่อันดับ โดยกำหนดค่า x = 0 แล้วหาค่า y จากสมการ และกำหนดค่า y = 0 แล้วหาค่า x จากสมการ
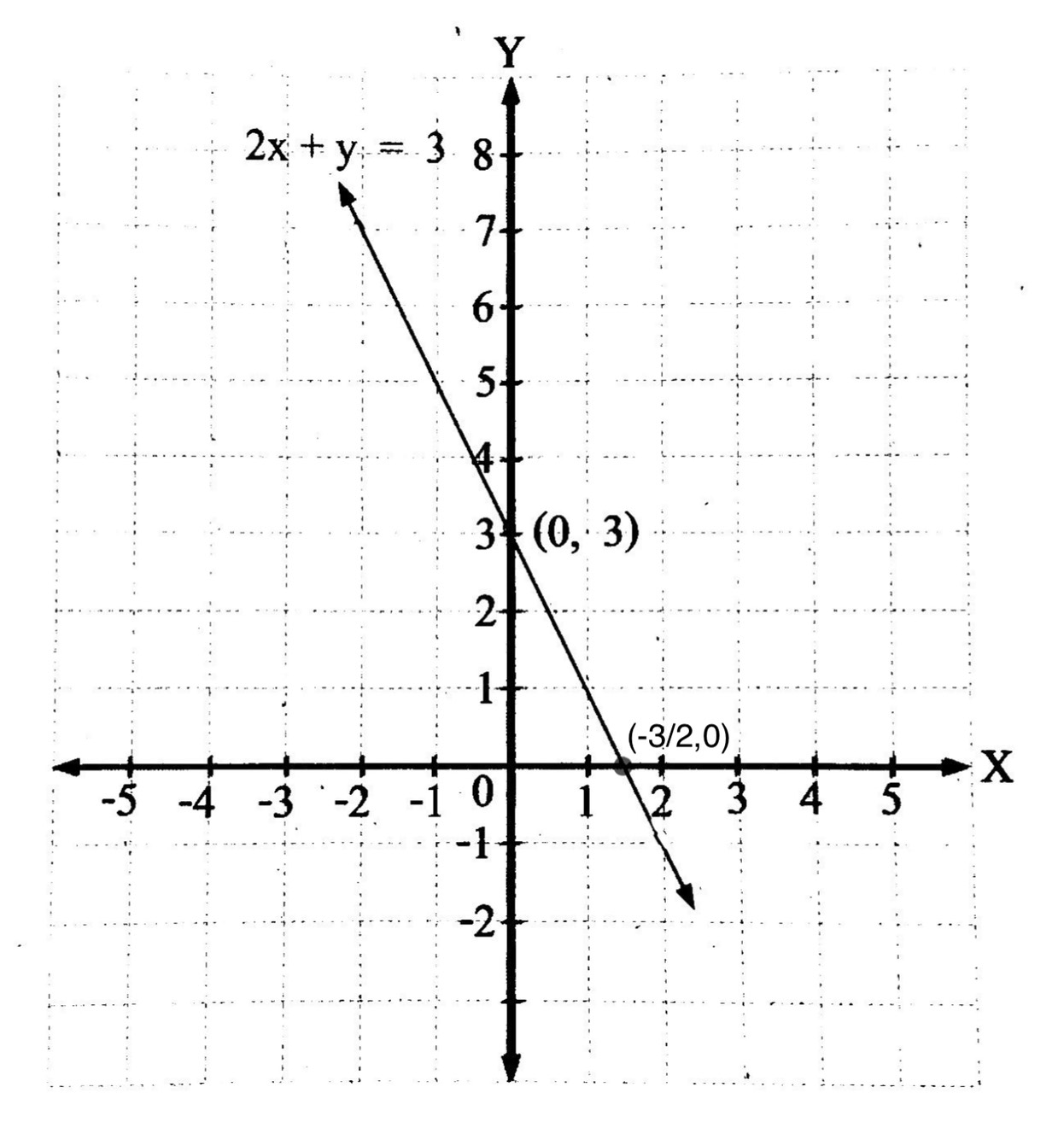
ตัวอย่าง จงเขียนกราฟของสมการ 2x + y = 3

จะได้กราฟของสมการ 2x + y = 3 เป็นดังนี้
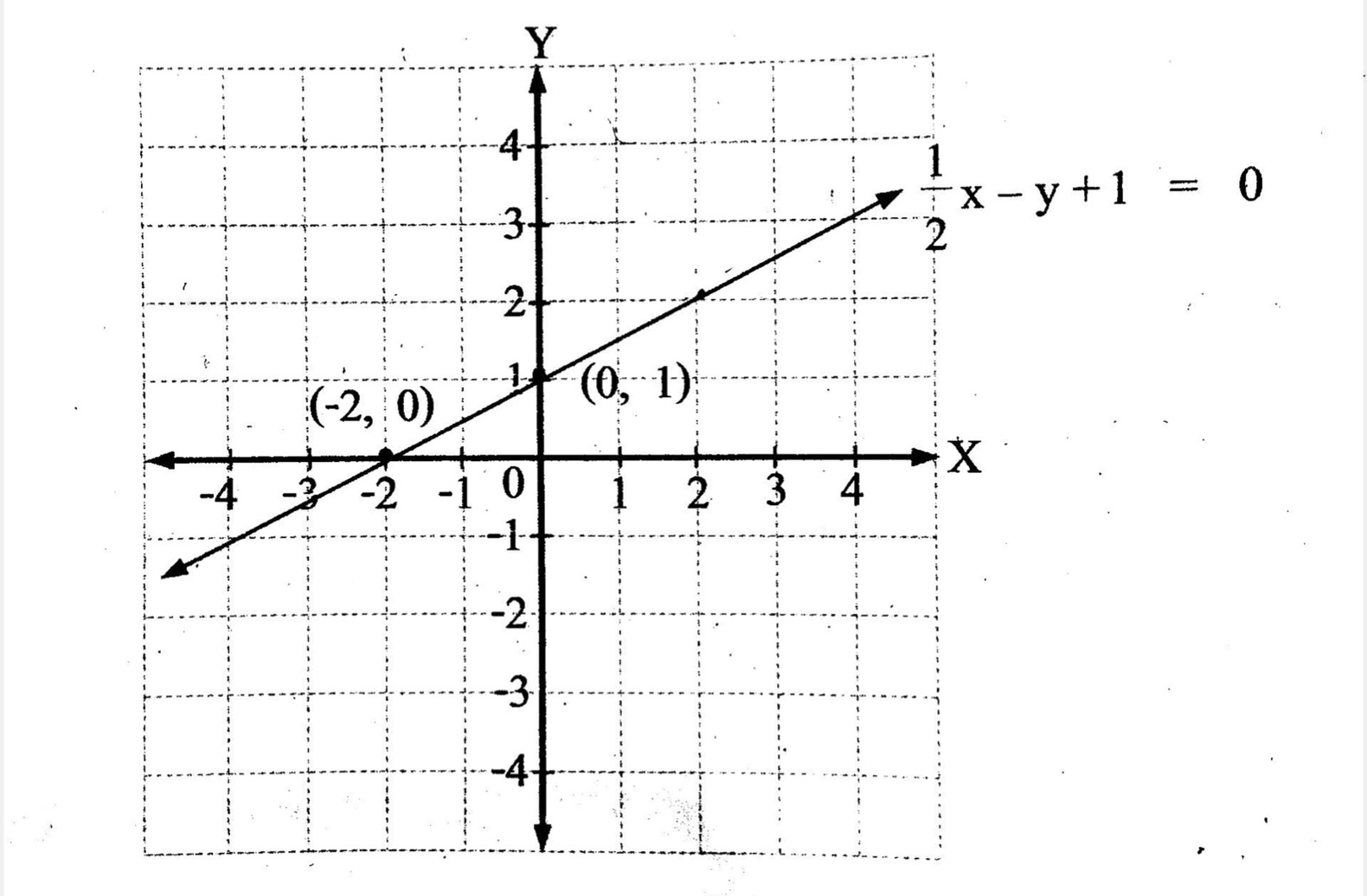
ตัวอย่าง จงเขียนกราฟของสมการ – y + 1=0

จะได้กราฟของสมการ – y + 1 = 0 เป็นดังนี้