บทความนี้จะเป็นการสอนวิธีการเขียน กราฟของความสัมพันธ์เชิงเส้น ซึ่งทำได้โดยการหาความสัมพันธ์ของจำนวนสองจำนวน เขียนให้อยู่ในรูปคู่อันดับ และเขียนกราฟแสดงความสัมพันธ์ข้างต้น ซึ่งน้องๆสามารถศึกษาการเขียนกราฟของความสัมพันธ์เชิงเส้นเพิ่มเติมได้ที่ ⇒⇒ กราฟของความสัมพันธ์เชิงเส้น ⇐⇐
คู่อันดับ
กราฟของความสัมพันธ์เชิงเส้น เขียนแสดงความเกี่ยวข้องของปริมาณสองปริมาณที่กำหนดให้ โดยความสัมพันธ์ระหว่างปริมาณสองปริมาณที่พบในชีวิตประจำวัน เช่น ปริมาณของน้ำประปาที่ใช้กับค่าน้ำ ปริมาณเวลาในการใช้โทรศัพท์กับค่าโทรศัพท์ ระยะทางที่โดยสารรถประจำทางปรับอากาศกับค่าโดยสาร ปริมาณของกระแสไฟฟ้ากับค่าไฟฟ้า เป็นต้น เราสามารถเขียนแสดงความสัมพันธ์เหล่านี้ในรูปตาราง แผนภาพ คู่อันดับ รวมทั้งแสดงในรูปของกราฟได้ ซึ่งในหัวข้อนี้ เราจะทำความรู้จักกับคู่อันดับกันก่อนนะคะ
คู่อันดับ เขียนแทนด้วยสัญลักษณ์ (a, b) อ่านว่า คู่อันดับเอบี
เรียก a ว่าสมาชิกตัวที่หนึ่งหรือสมาชิกตัวหน้า ซึ่งเป็นสมาชิกกลุ่มที่ 1
เรียก b ว่าสมาชิกตัวที่สองหรือสมาชิกตัวหลัง ซึ่งเป็นสมาชิกของกลุ่มที่ 2
ตัวอย่างที่ 1 พิจารณาตารางต่อไปนี้
| จำนวนน้ำตาล (ถุง) | 1 | 2 | 3 | 4 | 5 |
| ราคา (บาท) | 15 | 30 | 45 | 60 | 75 |
เขียนคู่อันดับ แสดงการอ่าน และบอกความหมาย
(1, 15) อ่านว่า คู่อันดับหนึ่ง สิบห้า หมายความว่า น้ำตาล 1 ถุง ราคา 15 บาท
(2, 30) อ่านว่า คู่อันดับสอง สามสิบ หมายความว่า น้ำตาล 2 ถุง ราคา 30 บาท
(3, 45) อ่านว่า คู่อันดับสาม สี่สิบห้า หมายความว่า น้ำตาล 3 ถุง ราคา 45 บาท
(4, 60) อ่านว่า คู่อันดับสี่ หกสิบ หมายความว่า น้ำตาล 4 ถุง ราคา 60 บาท
(5, 75) อ่านว่า คู่อันดับห้า เจ็ดสิบห้า หมายความว่า น้ำตาล 5 ถุง ราคา 75 บาท
สมบัติของคู่อันดับ
- (a, b) ≠ (b, a) ยกเว้น a = b
- (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d
กราฟของคู่อันดับ
กราฟของคู่อันดับ เป็นกราฟที่แสดงความสัมพันธ์ระหว่างสมาชิก 2 กลุ่ม
เขียนเส้นจำนวนในแนวนอนและแนวตั้ง ให้ตัดกันเป็นมุมฉากที่จุดซึ่งแทนศูนย์ (0) ดังต่อไปนี้
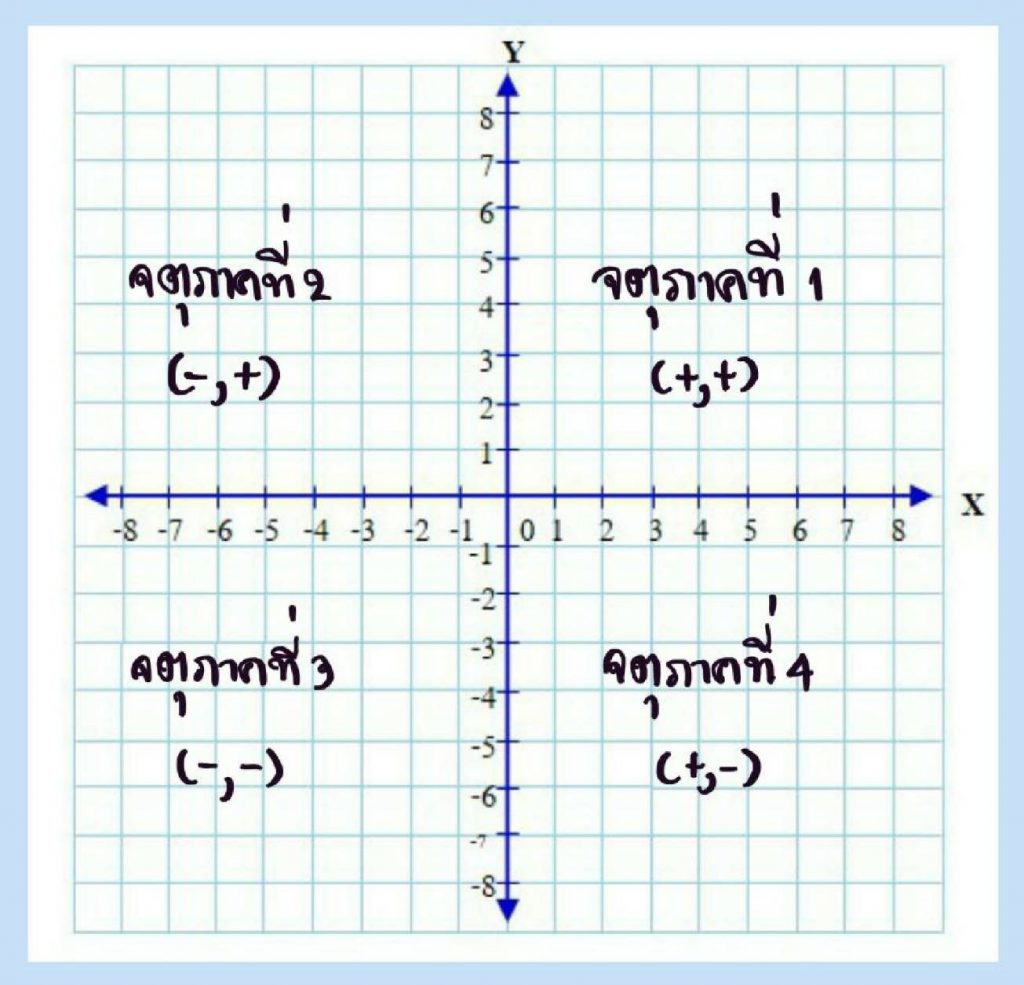
จุดที่เส้นจำนวนทั้งสองตัดกันเรียกว่า จุดกำเนิด นิยมแทนด้วย 0
เส้นจำนวนในแนวนอนเรียกว่า แกนนอน หรือ แกน X และเส้นจำนวนในแนวตั้งเรียกว่า แกนตั้ง หรือ แกน Y
แกน X และ แกน Y อยู่บนระนาบเดียวกัน และแบ่งระนาบออกเป็น 4 ส่วน เรียกแต่ละส่วนว่า จตุภาค
จตุภาคที่ 1 ระยะตามแกน X และ แกน Y เป็นจำนวนบวกทั้งคู่
จตุภาคที่ 2 ระยะตามแกน X เป็นจำนวนลบ และระยะตามแกน Y เป็นจำนวนบวก
จตุภาคที่ 3 ระยะตามแกน X และ แกน Y เป็นจำนวนลบทั้งคู่
จตุภาคที่ 4 ระยะตามแกน X เป็นจำนวนบวก และระยะตามแกน Y เป็นจำนวนลบ
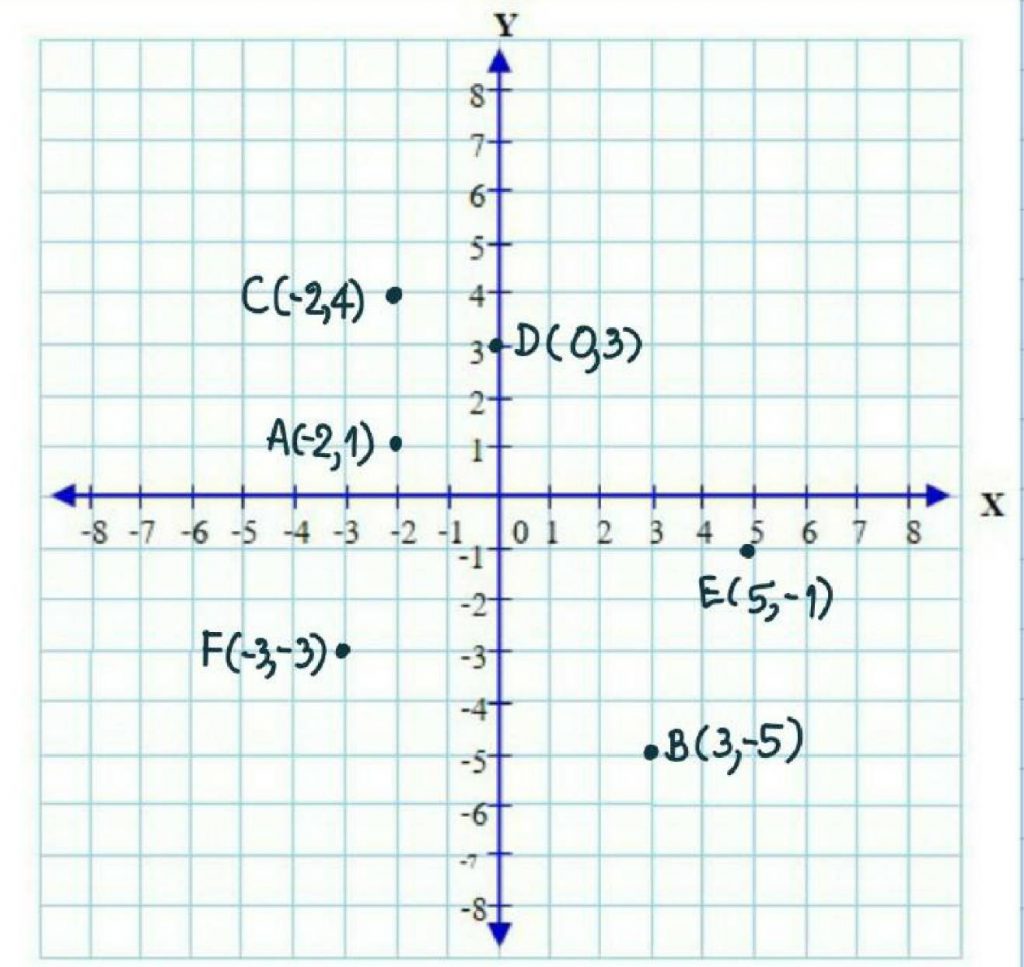
ตัวอย่างที่ 2 จงลงจุดต่อไปนี้ บนระนาบ X, Y
1. A(-2, 1), B(3, -5), C(-2, 4), D(0,3), E(5, -1) และ F(-3, -3)
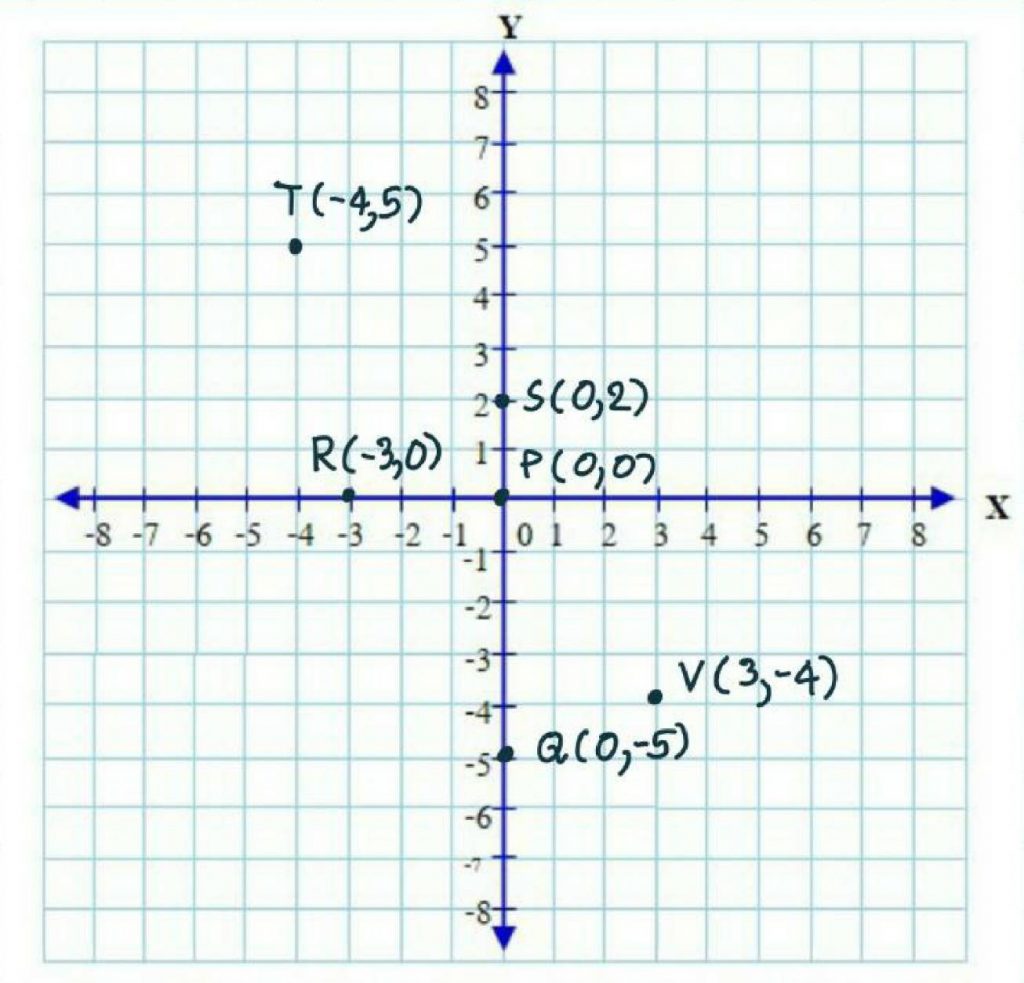
2. P(0, 0), Q(0, -5), R(-3, 0), S(0,2), T(-4, 5) และ V(3, -4)
ความสัมพันธ์เชิงเส้น
ความสัมพันธ์เชิงเส้น แสดงความสัมพันธ์ของปริมาณ 2 ปริมาณ ที่มีกราฟอยู่ในแนวเส้นตรงเดียวกัน เรียกความสัมพันธ์ลักษณะเช่นนี้ว่า “ความสัมพันธ์เชิงเส้น”
- ความสัมพันธ์เชิงเส้นเป็นความสัมพันธ์ของปริมาณสองปริมาณ ที่มีกราฟอยู่ในแนวเส้นตรงเดียวกัน
- ความสัมพันธ์เชิงเส้นระหว่างปริมาณสองปริมาณ อาจมีกราฟอยู่ในแนวเส้นตรงเดียวกันเป็นช่วงๆ ไม่จำเป็นต้องเป็นแนวเส้นตรงเดียวกันทั้งหมดก็ได้
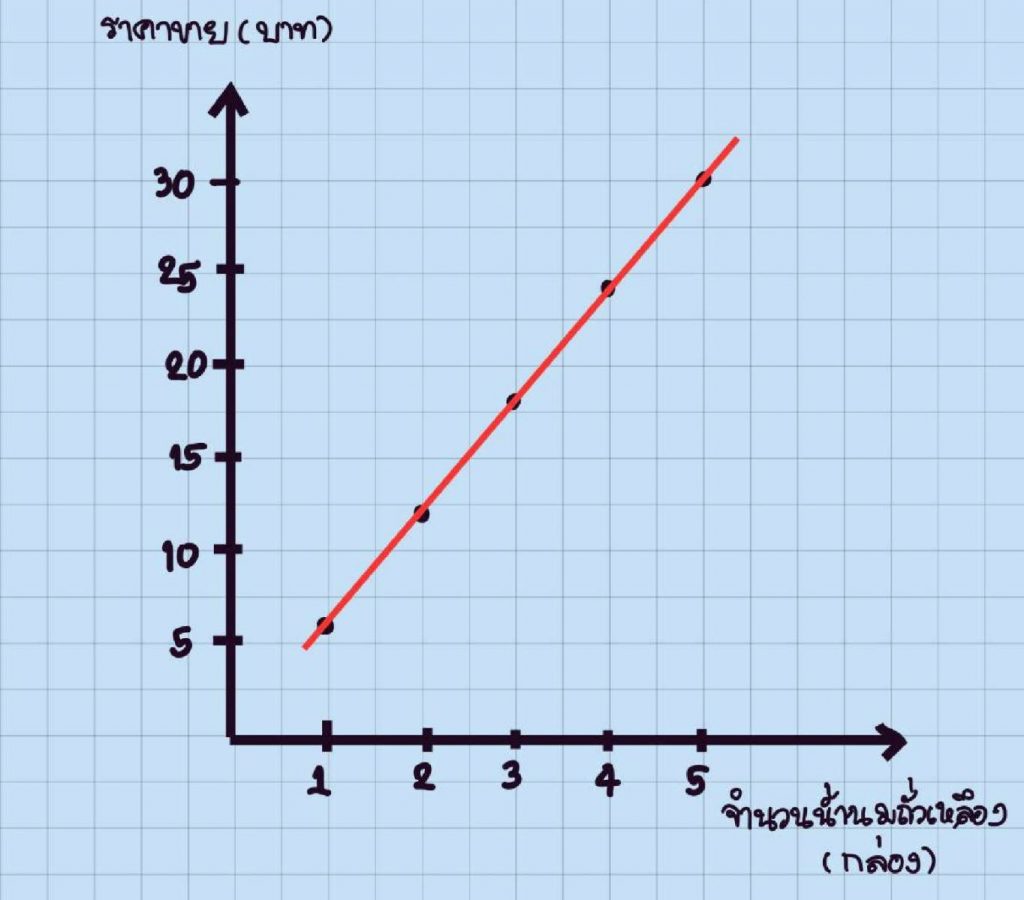
ตัวอย่างที่ 3 จงเขียนคู่อันดับและกราฟของคู่อันดับของความสัมพันธ์ของจำนวนนมถั่วเหลืองกับราคาขาย
| จำนวนนมถั่วเหลือง (กล่อง) | 1 | 2 | 3 | 4 | 5 |
| ราคาขาย (บาท) | 6 | 12 | 18 | 24 | 30 |
วิธีทำ จากข้อมูลในตารางสามารถจับคู่ระหว่างจำนวนนมถั่วเหลืองกับราคาขายได้ 5 คู่ คือ 1 กับ 6, 2 กับ 12, 3 กับ 18, 4 กับ 24, 5 กับ 30
เขียนแสดงการจับคู่โดยใช้สัญลักษณ์ ได้ดังนี้ (1, 6), (2, 12), (3, 18), (4, 24) และ (5, 30)
ถ้านำความสัมพันธ์ของจำนวนนมถั่วเหลืองกับราคาขายมาเขียนให้อยู่ในรูป (1, 6), (2, 12), (3, 18), (4, 24), (5, 30) เราเรียกสัญลักษณ์นี้ว่า “คู่อันดับ” และเรียกจำนวนนมถั่วเหลืองกับราคาขายในแต่ละคู่อันดับว่า “สมาชิกของคู่อันดับ” โดยสมาชิกตัวหน้าแทนจำนวนนมถั่วเหลืองและสมาชิกตัวหลังแทนราคาขาย เช่น
- (1, 6) อ่านว่า คู่อันดับหนึ่งหก มี 1 เป็นสมาชิกตัวหน้า และ 6 เป็นสมาชิกตัวหลัง หมายความว่า นมถั่วเหลือง 1 กล่อง ราคา 6 บาท
- (2, 12) อ่านว่า คู่อันดับสอง สิบสอง มี 2 เป็นสมาชิกตัวหน้า และ 12 เป็นสมาชิกตัวหลัง หมายความว่า นมถั่วเหลือง 2 กล่อง ราคา 12 บาท
- (3, 18) อ่านว่า คู่อันดับสามสิบแปด มี 3 เป็นสมาชิกตัวหน้า และ 18 เป็นสมาชิกตัวหลัง หมายความว่า นมถั่วเหลือง 3 กล่อง ราคา 18 บาท
- (4, 24) อ่านว่า คู่อันดับสี่ ยี่สิบสี่ มี 4 เป็นสมาชิกตัวหน้า และ 24 เป็นสมาชิกตัวหลัง หมายความว่า นมถั่วเหลือง 4 กล่อง ราคา 24 บาท
- (5, 30) อ่านว่า คู่อันดับห้า สามสิบ มี 5 เป็นสมาชิกตัวหน้า และ 30 เป็นสมาชิกตัวหลัง หมายความว่า นมถั่วเหลือง 5 กล่อง ราคา 30 บาท
คำถามเพิ่มเติม : คู่อันดับ (1, 6) กับ (6, 1) เหมือนกันหรือไม่ เพราะอะไร
อธิบายเพิ่มเติม : ถ้าเขียนความสัมพันธ์ของจำนวนนมถั่วเหลืองกับราคาขายเป็น (6, 1) จะได้ว่า นมถั่วเหลือง 6 กล่อง ราคา 1 บาท พบว่า ความหมายของคู่อันดับดังกล่าวจะเปลี่ยนไปจากเดิม ดังนั้นลำดับของสมาชิกแต่ละตัวในคู่อันดับมีความสำคัญในเงื่อนไขหรือข้อตกลงนั้น
เขียนกราฟของคู่อันดับ ได้ดังนี้
ตัวอย่างที่ 4 จงเขียนกราฟแสดงความสัมพันธ์ระหว่างจำนวนมะละกอ และราคาขายจากตารางที่กำหนดให้
| จำนวนมะละกอ (ผล) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| ราคาขาย (บาท) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
วิธีทำ จากตารางเขียนคู่อันดับแสดงความสัมพันธ์ระหว่างจำนวนมะละกอกับราคาขาย ได้ดังนี้
(1,10), (2,20), (3,30), (4,40), (5,50), (6,60) และ (7,70)
เมื่อกำหนดให้แกน X แสดงจำนวนมะละกอ และแกน Y แสดงราคาขาย จะได้กราฟแสดงความสัมพันธ์ระหว่างมะละกอกับราคาขาย ได้ดังนี้
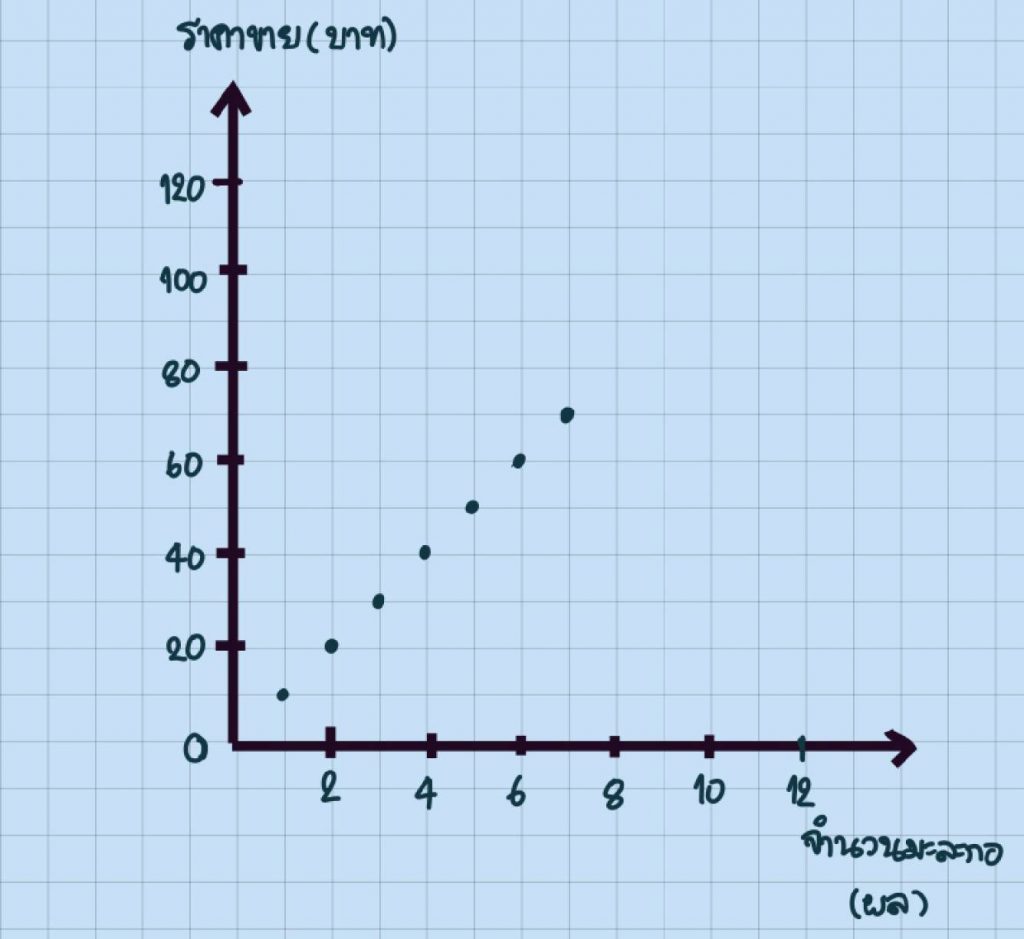
หมายเหตุ : เนื่องจากจำนวนมะละกอเป็นจำนวนบวกกราฟแสดงความสัมพันธ์จึงอยู่ในจตุภาคที่ 1 เท่านั้น
ตัวอย่างที่ 5 กำหนดกราฟแสดงจำนวนมังคุดที่ชาวสวนเก็บส่งขายได้ตั้งแต่วันที่ 1 ถึงวันที่ 10 ของเดือนพฤษภาคม
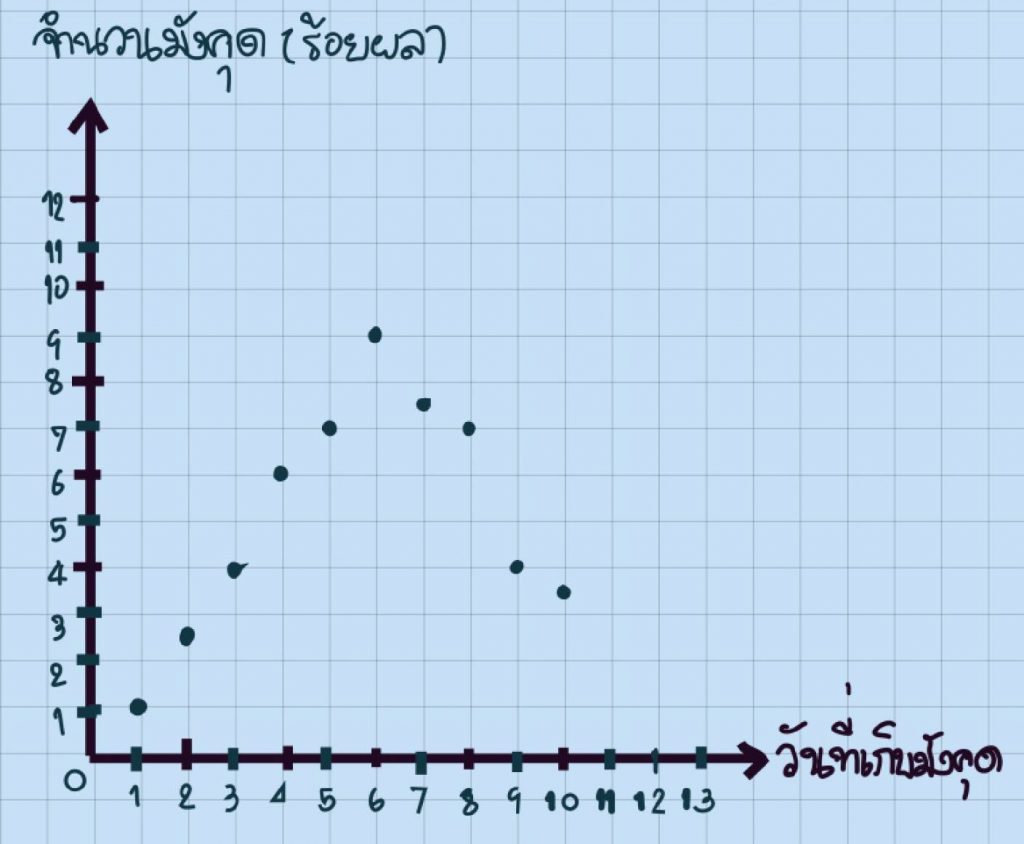
จงตอบคำถามต่อไปนี้
- วันที่ 1 เก็บมังคุดส่งขายได้เท่าไร
ตอบ 100 ผล
- วันที่เท่าไรเก็บมังคุดส่งขายได้มากที่สุด เก็บได้เท่าไร
ตอบ วันที่ 6 เก็บมังคุดได้ 900 ผล
- วันที่เท่าไรบ้างที่เก็บมังคุดได้เป็นจำนวนเท่ากัน และเก็บได้เท่าไรบ้าง
ตอบ วันที่ 3 กับ 9 เก็บได้ 400 ผล และวันที่ 5 กับวันที่ 8 เก็บได้ 700 ผล
- วันที่เท่าไรที่จำนวนมังคุดที่เก็บส่งขายเริ่มมีจำนวนลดลง
ตอบ วันที่ 7
- จำนวนมังคุดที่เก็บส่งขายในรอบ 10 วันมีการเปลี่ยนแแปลงอย่างไร
ตอบ จำนวนมังคุดที่เก็บส่งขายได้ใน 6 วันแรก เพิ่มขึ้นโดยตลอด และมีจำนวนมากที่สุดถึง 900 ผล ในวันที่ 6 หลังจากนั้นมีจำนวนลดลงเรื่อย ๆ จนถึงวันที่ 10


















