โจทย์ปัญหาเกี่ยวกับอัตราส่วน สัดส่วน และร้อยละ
บทความนี้ ได้รวบรวม โจทย์ปัญหาเกี่ยวกับอัตราส่วน สัดส่วน และร้อยละ ซึ่งการแก้โจทย์ปัญหานั้น น้องๆจะต้องอ่านทำความเข้าใจกับโจทย์ให้ละเอียด และพิจารณาอย่างรอบคอบว่าโจทย์กำหนดอะไรมาให้บ้างและโจทย์ต้องการให้หาอะไร จากนั้นจะสามารถหาค่าของสิ่งที่โจทย์ต้องการได้โดยใช้ความรู้เรื่องการคูณไขว้ สัดส่วน และร้อยละ ก่อนจะเรียนรู้เรื่องนี้ น้องๆจำเป็นต้องมีความรู้ในเรื่อง สัดส่วน เพิ่มเติมได้ที่ ⇒⇒ สัดส่วน ⇐⇐
โจทย์ปัญหาเกี่ยวกับสัดส่วน
ตัวอย่างที่ 1 อัตราส่วนของอายุของนิวต่ออายุของแนน เป็น 2 : 3 อัตราส่วนของอายุของแนนต่ออายุของมิ้น เป็น 9 : 7 ถ้านิวอายุ 42 ปี แล้วมิ้นอายุเท่าไร
วิธีทำ ให้มิ้นอายุ x ปี
อัตราส่วนของอายุของนิวต่ออายุของแนน เป็น 2 : 3 = 2 × 3 : 3 × 3 = 6 : 9
อัตราส่วนของอายุของแนนต่ออายุของมิ้น เป็น 9 : 7
จะได้ อัตราส่วนของอายุของนิวต่ออายุของแนนต่ออายุของมิ้น เป็น 6 : 9 : 7
ถ้านิวอายุ 42 ปี มิ้นจะอายุ x ปี
เขียนสัดส่วนได้ดังนี้
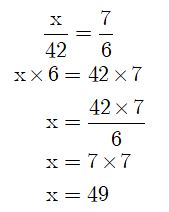
ดังนั้น มิ้นอายุ 49 ปี
ตัวอย่างที่ 2 แมนวางแผนเพื่อปลูกต้นมะม่วงกับต้นมะขามเป็นแนวรั้ว โดยปลูกต้นมะม่วงสลับกับต้นมะขามเป็นอัตราส่วน เป็น 2 : 5 เมื่อแมนปลูกเสร็จแล้วปรากฏว่ามีต้นมะขาม 95 ต้น จงหาว่าแมนปลูกต้นมะม่วงทั้งหมดกี่ต้น
วิธีทำ ให้แมนปลูกต้นมะม่วงทั้งหมด x ต้น
อัตราส่วนของจำนวนต้นมะม่วงต่อจำนวนต้นมะขาม เป็น 2 : 5 หรือ
ถ้าแมนปลูกต้นมะขามทั้งหมด 95 ต้น
อัตราส่วนใหม่ คือ x : 95 หรือ
เขียนสัดส่วนได้ดังนี้
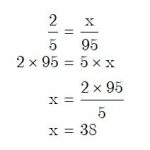
ดังนั้น แมนปลูกต้นมะม่วงทั้งหมด 38 ต้น
โจทย์ปัญหาเกี่ยวกับร้อยละ
ตัวอย่างที่ 3 โรงเรียนแห่งหนึ่งมีนักเรียน 2,600 คน มีนักเรียนชายคิดเป็น 44 % ของนักเรียนทั้งหมดจะมีนักเรียนหญิงกี่คน
วิธีทำ 1) ทำความเข้าใจโจทย์
– สิ่งที่โจทย์ถาม คือ จำนวนนักเรียนหญิงกี่คน
– สิ่งที่โจทย์กำหนด คือ โรงเรียนแห่งหนึ่งมีนักเรียน 2,600 คน มีนักเรียนชาย คิดเป็น 44 % ของนักเรียนทั้งหมด จะได้ว่ามีจำนวนนักเรียนหญิง 56% ของนักเรียนทั้งหมด
2) เขียนสัดส่วนแสดงอัตราส่วนโดยให้ลำดับของสิ่งที่เปรียบเทียบในแต่ละอัตราส่วนเป็นลำดับเดียวกัน
นักเรียนชายคิดเป็น 44 % จะมีนักเรียนหญิง 56 % ของนักเรียนทั้งหมด
ให้มีนักเรียนหญิง a คน
อัตราส่วนของจำนวนนักเรียนหญิงต่อจำนวนนักเรียนทั้งหมด เป็น

3) แก้สมการหาค่าตัวแปร
เขียนเป็นสัดส่วนได้ดังนี้
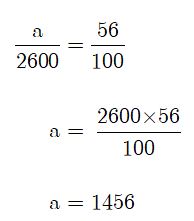
ดังนั้น จะมีนักเรียนหญิง 1,456 คน
ตัวอย่างที่ 4 แม่ค้าขายเงาะลงทุนทั้งสิ้น 1,200 บาท ปรากฏว่าขายเงาะแล้วได้กำไร 20% อยากทราบว่าแม่ค้าขายเงาะได้กำไรเป็นเงินเท่าไร
วิธีทำ 1) ทำความเข้าใจโจทย์
– สิ่งที่โจทย์ถาม คือ แม่ค้าขายเงาะได้กำไรเป็นเงินเท่าไร
– สิ่งที่โจทย์กำหนด คือแม่ค้าขายเงาะลงทุนทั้งสิ้น 1,200 บาท ขายแล้วได้กำไร 20%
2) เขียนสัดส่วนแสดงอัตราส่วนโดยให้ลำดับของสิ่งที่เปรียบเทียบในแต่ละอัตราส่วนเป็นลำดับเดียวกัน
ให้แม่ค้าขายเงาะได้กำไรเป็นเงิน y บาท
ขายเงาะได้กำไร คิดเป็น 20% =

3) แก้สมการหาค่าตัวแปร
เขียนเป็นสัดส่วนได้ดังนี้
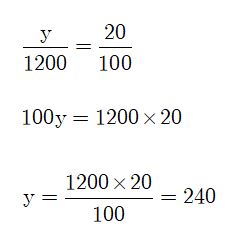
ดังนั้น แม่ค้าขายเงาะได้กำไรเป็นเงิน 240 บาท
ตัวอย่างที่ 5 นาวิทซื้อรถยนต์คันหนึ่ง จ่ายเงินมัดจำไป 75,000 บาท คิดเป็น 15% ของราคารถยนต์คันนี้ จงหาว่ารถยนต์คันนี้ราคาเท่าไร
วิธีทำ ให้นาวิทซื้อรถยนต์คันนี้ราคา x บาท
จ่ายเงินมัดจำไป 75,000 บาท
เงินมัดจำที่จ่ายไปคิดเป็น 15% =
เขียนสัดส่วนได้ดังนี้
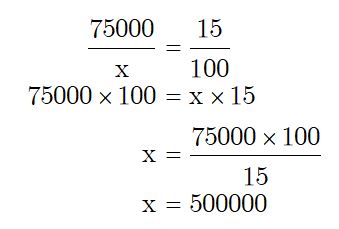
ดังนั้น นาวิทซื้อรถยนต์คันนี้ ราคา 500,000 บาท
ตัวอย่างที่ 6 ร้านขายเครื่องใช้ไฟฟ้าแห่งหนึ่งปิดราคาพัดลมไว้ 560 บาท โดยคิดเอากำไร 40 % ต่อมาขายไปเป็นเงิน 480 บาท จะได้กำไรกี่เปอร์เซ็นต์
วิธีทำ คิดเอากำไร 40 % หมายความว่า ปิดราคา 140 บาท จากราคาทุน 100 บาท
ให้พัดลมมีราคาทุน m บาท
เขียนสัดส่วนได้ดังนี้
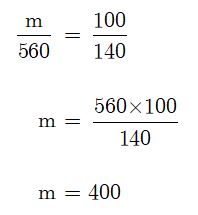
เพราะฉะนั้น ราคาทุน เท่ากับ 400 บาท
ขายไปเป็นเงิน 480 บาท
เพราะฉะนั้น กำไร 480 – 400 = 80 บาท
ให้ได้กำไร n%
เขียนสัดส่วนได้ดังนี้
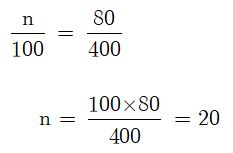
ดังนั้น จะได้กำไร 20%
โจทย์ปัญหาเกี่ยวกับภาษี
ก่อนที่น้องๆจะไปเรียนรู้ โจทย์ปัญหาเกี่ยวกับภาษี ให้น้องๆได้ศึกษาความหมายของคำจำกัดความต่อไปนี้
เงินได้พึงประเมิน หมายถึง เงินรายได้ของผู้เสียภาษีก่อนหักค่าใช่จ่ายและค่าลดหย่อน
ค่าใช้จ่าย หมายถึง รัฐบาลให้ผู้มีรายได้หักค่าใช้จ่ายได้ร้อยละ 40 ของเงินพึงประเมิน แต่ไม่เกิน 60,000 บาท
ค่าลดหย่อน หมายถึง ผู้มีเงินรายได้สามารถหักค่าลดหย่อนออกจากเงินได้พึงประเมินได้อีก เช่น ค่าลดหย่อนสำหรับบุคคลที่มีเงินรายได้ ค่าลดหย่อนสำหรับบุตร ค่าลดหย่อนสำหรับเบี้ยประกัน และค่าลดหย่อนสำหรับเงินบริจาค เป็นต้น
เงินได้สุทธิ หมายถึง ได้พึงประเมินหลังจากที่หักค่าใช้จ่ายและหักค่าลดหย่อนแล้ว เงินได้สุทธินี้ จะนำไปเป็นเงินคำนวณภาษีที่ต้องเสียให้แก่รัฐตามอัตราที่กำหนดไว้
ตัวอย่างที่ 7 วีระทำงานบริษัทแห่งหนึ่งได้รับเงินเดือนเดือนละ 35,000 บาท มีภรรยาที่ไม่ได้ทำงาน และมีบุตร 2 คน กำลังเรียนอยู่ชั้น ม.1 และ ม.2 เขาจะเสียภาษีเท่าไร ( ค่าลดหย่อนผู้มีเงินได้ 30,000 บาท ค่าลดหย่อนคู่สมรส 30,000 บาท และค่าลดหย่อนบุตรกรณีศึกษาอยู่ในประเทศ คนละ 17,000 บาท กรณีที่ไม่ได้ศึกษาหรือศึกษาต่อต่างประเทศคนละ 15,000 บาท )
วิธีทำ วีระมีรายได้ปีละ 35,000 × 12 = 420,000 บาท
หักค่าใช้จ่าย 40% ของเงินได้พึงประเมิน × 420,000 = 168,000 บาท
เนื่องจากหักค่าใช้จ่าย 40% ของเงินได้พึงประเมินเกิน 60,000 บาท
ดังนั้น หักเพียง 60,000 บาท
เหลือเงินได้พึงประเมิน 420,000 – 60,000 = 360,000 บาท
หักค่าลดหย่อนส่วนตัว 30,000 บาท
หักค่าลดหย่อนภรรยา 30,000 บาท
หักค่าลดหย่อนบุตร 17,000 × 2 = 34,000 บาท
รวมหักค่าลดหย่อน 30,000 + 30,000 + 34,000 = 94,000 บาท
เงินได้สุทธิที่ต้องเสียภาษี 360,000 – 94,000 = 266,000 บาท
เงินได้สุทธิ 150,000 บาทแรก ยกเว้นภาษี
ส่วนที่เกิน 150,000 บาท แต่ไม่เกิน 500,000 บาท เสียภาษี 10%
จะได้ว่า เงินได้สุทธิ 266,000 – 150,000 = 116,000 บาท
ดังนั้น เสียภาษี × 116,000 = 11,600 บาท
ตัวอย่างที่ 8 การิม เป็นโสด ทำงานได้เงินเดือนปีละ 300,000 บาท จ่ายเงินเข้ากองทุนสำรองเลี้ยงชีพปีละ 18,000 บาท ทำประกันชีวิตไว้โดยจ่ายเบี้ยประกันปีละ 12,000 บาท บริจาคเงิน 3,000 บาท จงหาว่า การิม ต้องจ่ายภาษีทั้งหมดกี่บาท
วิธีทำ รายได้ทั้งปี 300,000 บาท
หักค่าใช้จ่าย 40% ของเงินได้พึงประเมิน × 300,000 = 120,000 บาท
เนื่องจากหักค่าใช้จ่าย 40% ของเงินได้พึงประเมินเกิน 60,000 บาท
ดังนั้น หักเพียง 60,000 บาท
เหลือเงินได้พึงประเมิน 300,000 – 60,000 = 240,000 บาท
หักค่าลดหย่อนส่วนตัว 30,000 บาท
หักค่าเบี้ยประกันชีวิต 12,000 บาท
หักเงินสะสมเข้ากองทุนสำรองเลี้ยงชีพ 18,000 บาท
หักเงินบริจาคตามที่จ่ายจริง 3,000 บาท
รวมหักค่าลดหย่อน 30,000 + 12,000 + 18,000 + 3,000 = 63,000 บาท
เงินได้สุทธิที่ต้องเสียภาษี 240,000 – 63,000 = 177,000 บาท
เงินได้สุทธิ 150,000 บาทแรก ยกเว้นภาษี
ส่วนที่เกิน 150,000 บาท แต่ไม่เกิน 500,000 บาท เสียภาษี 10%
จะได้ว่า เงินได้สุทธิ 177,000 – 150,000 = 27,000 บาท
ดังนั้น เสียภาษี × 27,000 = 2,700 บาท
ตัวอย่างที่ 9 เกรซมีเงินได้จากบริษัทแห่งหนึ่ง เดือนละ 20,000 บาท ตลอดปีภาษี 2554 ถูกหักเงินสะสมเข้ากองทุนสำรองเลี้ยงชีพ 3% ของเงินเดือน ถูกหักเงินสมทบเข้ากองทุนประกันสังคม รวมทั้งปี 9,000 บาท จงคำนวณภาษีของเกรซ
วิธีทำ เกรซมีรายได้ปีละ 20,000 × 12 = 240,000 บาท
หักค่าใช้จ่าย 40% ของเงินได้พึงประเมิน × 240,000 = 96,000 บาท
เนื่องจากหักค่าใช้จ่าย 40% ของเงินได้พึงประเมินเกิน 60,000 บาท
ดังนั้น หักเพียง 60,000 บาท
เหลือเงินได้พึงประเมิน 240,000 – 60,000 = 180,000 บาท
หักค่าลดหย่อนส่วนตัว 30,000 บาท
หักเงินสะสมเข้ากองทุนสำรองเลี้ยงชีพ 3% ของเงินเดือน × 20,000 = 600 บาท
ตลอดทั้งปี คิดเป็นเงิน 600 × 12 = 7,200 บาท
หักเงินสมทบเข้ากองทุนประกันสังคม รวมทั้งปี เป็นเงิน 9,000 บาท
รวมหักค่าลดหย่อน 30,000 + 7,200 + 9,000 = 46,200 บาท
เงินได้สุทธิที่ต้องเสียภาษี 180,000 – 46,200 = 133,800 บาท
เงินได้สุทธิ 150,000 บาทแรก ยกเว้นภาษี
ดังนั้น เกรซได้รับการยกเว้นไม่ต้องเสียภาษี
เมื่อน้องๆเรียนรู้เรื่อง โจทย์ปัญหาเกี่ยวกับอัตราส่วน สัดส่วน และร้อยละ จะทำให้น้องๆได้ฝึกการวิเคราะห์โจทย์ปัญหา และตีความจากโจทย์ เพื่อหาคำตอบที่ถูกต้อง จากตัวอย่างหลายๆตัวอย่าง ทำให้น้องๆ สามารถหาคำตอบ ได้อย่างรวดเร็วและแม่นยำ
คลิปวิดีโอ โจทย์ปัญหาเกี่ยวกับอัตราส่วน สัดส่วน และร้อยละ
คลิปวิดีโอนี้ได้รวบรวม โจทย์ปัญหาเกี่ยวกับอัตราส่วน สัดส่วน และร้อยละ โดยแสดงวิธีคิดไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค รวมถึงการอธิบาย ตัวอย่าง และสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย



















