โจทย์ปัญหาการนําเสนอข้อมูล

บทความนี้จะยกตัวอย่างเกี่ยวกับโจทย์ปัญหาการนำเสนอข้อมูลให้น้องๆทราบถึงวิธีคิดหรือวิธีทำเพื่อหาคำตอบที่ถูกต้อง

tucksaga

Add LINE friends for one click to find article.

ในบทเรียนเรื่องการนำเสนอข้อมูล การเขียนนำข้อมูลมานำเสนอในรูปแบบต่างๆเช่น แผนภูมิแท่ง หรือกราฟเส้น เมื่อเราทำการศึกษาและสามารถอ่านข้อมูลจากส่งเหล่านั้นได้แล้ว บทเรียนต่อไปจะเป็นเรื่องของโจทย์ปัญหาในการนำเสนอข้อมูล ที่จะมาในรูปแบบของคำถามที่ต้องหาคำตอบจาก แผนภูมิแท่งหรือกราฟเส้นที่โจทย์กำหนดมานั่นเอง

โจทย์ปัญหาการนำเสนอข้อมูล ป.5

ในการแก้โจทย์ปัญหาทางคณิตศาสตร์เรื่องการนำเสนอข้อมูลนั้น คุณต้องมีพื้นฐานการอ่านข้อมูลจาก แผนภูมิ หรือกราฟก่อนจึงจะสามารถแก้ไขโจทย์และหาคำตอบออกมาได้อย่างถูกต้อง ยกตัวอย่างโจทย์ดังนี้

ตัวอย่างที่ 1 โจทย์ปัญหาแผนภูมิแท่ง

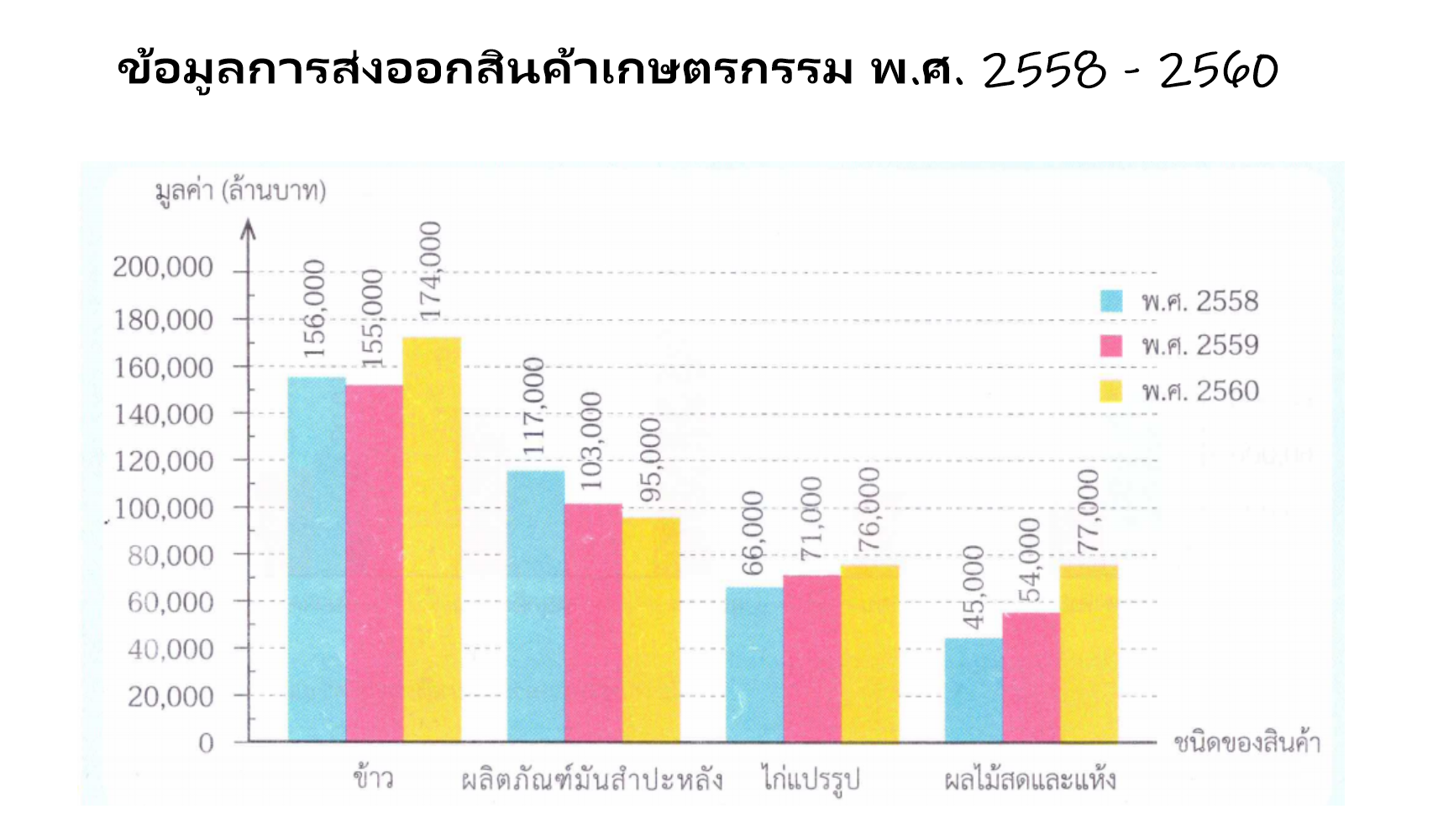
จากแผนภูมิแท่งจงคำถามต่อไปนี้

ข้อที่ 1.) พ.ศ.2558 – พ.ศ.2560 สินค้าที่มีมูลค่าการส่งออกมากที่สุดกับน้อยที่สุดต่างกันเท่าใด

วิธีทำ สินค้าที่มีมูลค้าการส่งออกมาที่สุดคือ ข้าว ในปี พ.ศ.2560 มีมูลค่าเท่ากับ 174,000 ล้านบาท และสินค้าที่มีมูลค่าการส่งออกที่น้อยที่สุดคือ ผลไม้สดและแห้ง ในปีพ.ศ. 2558 มีมูลค่าเท่ากับ 45,000 ล้านบาท

ดังนั้นมีมูลค่าต่างกันอยู่ที่ 174,000 – 45,000 = 129,000 ล้านบาท

ตอบ 129,000 ล้านบาท

ข้อที่ 2.) สินค้าที่มีมูลการส่งออกทั้งสามปีน้อยกว่า 200,000 ล้านบาทได้แก่อะไรบ้าง

วิธีทำ มูลค่าทั้งสามปีของข้าวเท่ากับ 156,000 + 155,000 + 174,000

= 485,000 ล้านบาท

มูลค่าทั้งสามปีของผลิตภันฑ์มันสำปะหลังเท่ากับ 117,000 + 103,000 + 95,000

= 315,000 ล้านบาท

มูลค่าทั้งสามปีของไก่แปรรูปเท่ากับ 66,000 + 71,000 + 76,000

= 143,000 ล้านบาท

มูลค่าทั้งสามปีของผลไม้สดและแห้งเท่ากับ 45,000 + 54,000 + 77,000

= 176,000 ล้านบาท

ตอบ ไก่แปรรูป และ ผลไม้สดและแห้ง

ตัวอย่างที่ 2 โจทย์ปัญหากราฟเส้น

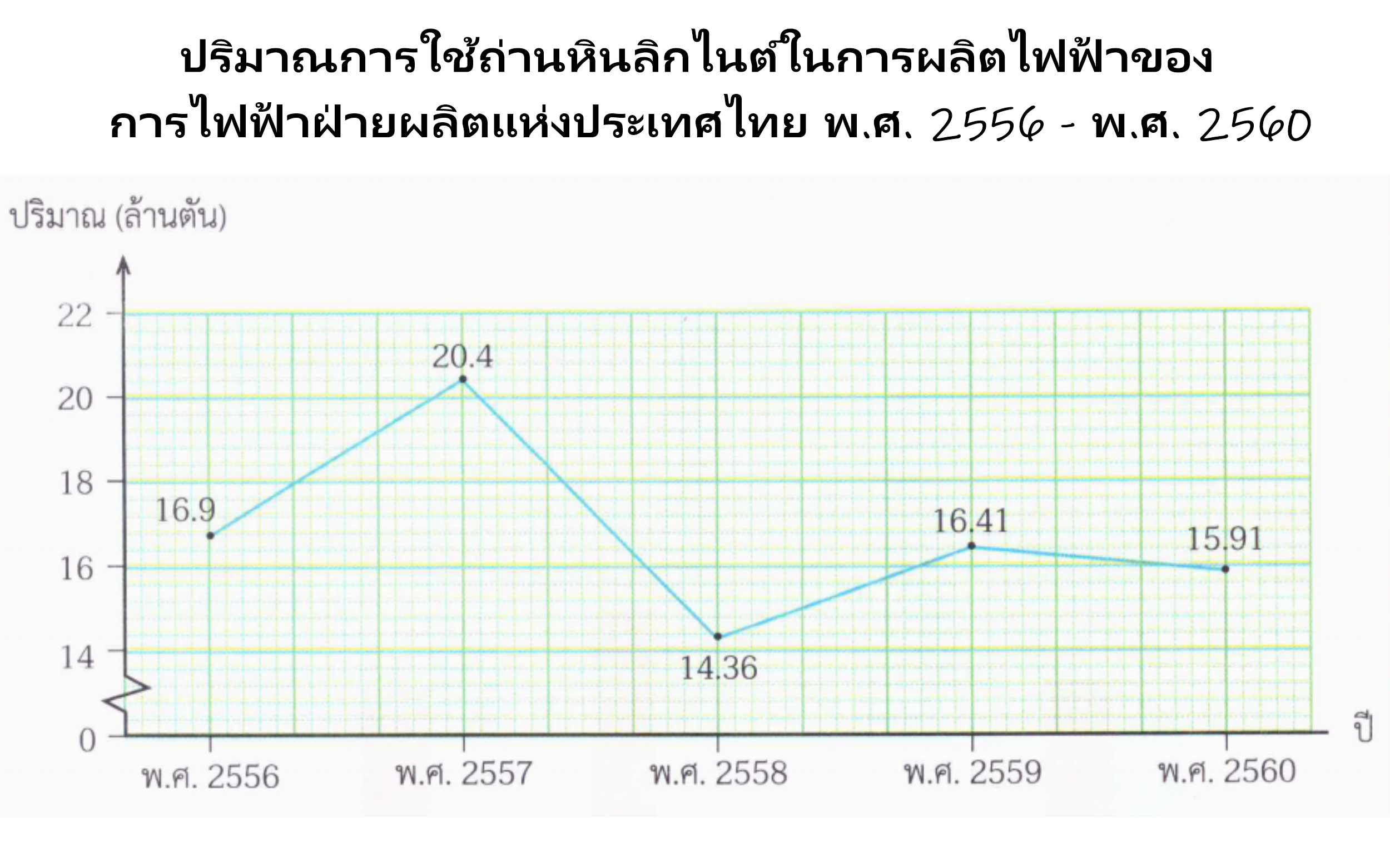
จากกราฟเส้นจงคำถามต่อไปนี้

คำถาม: ตั้งแต่ พ.ศ.2556 – พ.ศ.2560 การไฟฟ้าฝ่ายผลิตแห่งประเทศไทยใช้ถ่านหินลิกไนต์เฉลี่ยปีละกี่ล้านตัน

วิธีทำ นำปริมาณถ่านหินลิกไนต์ที่ใช้ไปของปีพ.ศ.2556 – พ.ศ.2560มารวมกัน

จะได้ 16.9 + 20.4 + 14.36 + 16.41 + 15.91 = 83.98 ล้านตัน

จากนั้นรวมปริมาณที่รวมกันข้างต้นเฉลี่ยให้กับ 5 ปี เท่าๆกัน

จะได้ 83.98 ล้านตัน ÷ 5 = 16.796 ล้านตัน

ตอบ เฉลี่ยปีละ 16.796 ล้านตัน

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

กาพย์ห่อโคลงประพาสธารทองแดง ถอดคำประพันธ์และคุณค่าในเรื่อง

หลังจากได้เรียนรู้ประวัติความเป็นมากันไปแล้ว บทเรียนในวันนี้จะพาน้อง ๆ ไปเรียนรู้การถอดคำประพันธ์ กาพย์ห่อโคลงประพาสธารทองแดง ว่ามีความหมายอย่างไรบ้าง ตัวบทที่ยกตัวอย่างมาในวันนี้จะเป็นเรื่องใด ถ้าพร้อมแล้วเราไปเรียนรู้วรรณคดีเรื่องนี้พร้อม ๆ กันเลยค่ะ ถอดคำประพันธ์ หัวลิงหมากกลางลิง ต้นลางลิงแลหูลิง ลิงไต่กระไดลิง

Present Continuous Tense

สวัสดีนักเรียนชั้นม.3 ที่น่ารักทุกคนค่า วันนี้เราจะไปเรียนรู้กันเรื่อง ” Present Continuous Tense” พร้อมทั้งตัวอย่างสถานการณ์ใกล้ตัว และข้อสอบวัดความเข้าใจหลังเรียนแบบปังๆกันจร้า หากพร้อมแล้วก็ไปลุยกันเลย เริ่มกับการใช้ Present Continuous Tense อธิบายสิ่งที่กำลังเกิดขึ้นอยู่ในขณะนั้น เช่น Danniel is playing a football at the moment.

Signal Words ในภาษาอังกฤษคืออะไร?

สวัสดีน้องๆ ม. 1 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้เรื่อง Signal Words ในภาษาอังกฤษว่าคืออะไร และเอาไปใช้ได้อย่างไรได้บ้าง เราไปเริ่มกันเลยครับ

การทดลองสุ่มและเหตุการณ์

บทความนี้ได้รวบรวมความรู้เรื่อง การทดลองสุ่มและเหตุการณ์ ซึ่งได้กล่าวถึงในลักษณะของความหมายและยกตัวอย่างประกอบ และอธิบายอย่างละเอียด ซึ่งก่อนจะเรียนเรื่อง การทดลองสุ่มและเหตุการณ์ น้องๆสามารถทบทวน ความน่าจะเป็น ได้ที่ ⇒⇒ ความน่าจะเป็น ⇐⇐ การทดลองสุ่ม การทดลองสุ่ม คือ การทดลองซึ่งทราบว่าผลลัพธ์ที่จะเกิดขึ้นอาจจะเป็นอะไรได้บ้าง แต่ไม่สามารถบอกได้อย่างถูกต้องแน่นอนว่าในแต่ละครั้งที่ทำการทดลอง ผลที่เกิดขึ้นจากการทดลองจะเป็นอะไรในบรรดาผลลัพธ์ที่อาจเป็นไปได้เหล่านั้น เช่น การโยนเหรียญซึ่งมีผลลัพธ์ที่จะเกิดขึ้นได้ 2 แบบ คือ หัวหรือก้อย เมื่อโยนเหรียญ

การหารทศนิยมในระดับชั้นป.5

บทความนี้จะกล่าวถึงหลักการหารทศนิยม 2 รูปแบบก็คือ การหารทศนิยมด้วยจำนวนเต็ม และการหารทศนิยมด้วยทศนิยม หลังจากที่น้องๆ ได้อ่านบทความนี้แล้ว รับรองว่าจะทำให้เข้าใจการหารทศนิยมได้มากขึ้นและสามารถนำวิธีคิดไปแก้โจทย์การหารทศนิยมได้

Phrasal Verbs

สวัสดีค่ะนักเรียนชั้นม.6 ที่รักทุกคนวันนี้เราจะไปเรียนรู้กันเรื่อง “Phrasal Verbs“ กันนะคะ ถ้าพร้อมแล้วก็ไปลุยกันโลด ความหมาย Phrasal Verbs Phrasal Verbs คือ คำกริยา โดยเป็นกริยาที่มีคำอื่นๆ อย่างเช่น คำบุพบท (Preposition) ร่วมกันส่วนใหญ่แล้ว Phrasal Verbs จะบอกถึงการกระทำ มักจะเจอในชีวิตประจำวันในสถานการณ์ทั่วไป ไม่เป็นทางการมาก ข้อดีคือจะทำให้ภาษาใกล้เคียงกับเจ้าของภาษามากขึ้นนั่นเองจ้า

โจทย์ปัญหาการนําเสนอข้อมูล

สารบัญ