อสมการค่าสัมบูรณ์

จากบทความที่ผ่านมา น้องๆได้ศึกษาเรื่องค่าสัมบูรณ์และการแก้อสมการไปแล้ว บทความนี้จะเป็นการเอาเนื้อหาของอสมการและค่าสัมบูรณ์มาปรับใช้ นั่นก็คือ เราจะแก้อสมการของค่าสัมบูรณ์นั่นเองค่ะ เรื่องอสมการค่าสัมบูรณ์น้องๆจะได้เจอในข้อสอบ O-Net แต่น้องๆไม่ต้องกังวลค่ะ ถ้าน้องๆเข้าใจหลักการและสมบัติของค่าสัมบูรณ์และอสมการน้องๆจะสามารถทำข้อสอบได้แน่นอน

supanaree

คณิต ม.4 พื้นฐาน, คณิตศาสตร์, คณิตศาสตร์ ม.4, ค่าสัมบูรณ์, ม.4, อสมการ, อสมการค่าสัมบูรณ์

Add LINE friends for one click to find article.

อสมการค่าสัมบูรณ์

อสมการค่าสัมบูรณ์ คือ อสมการที่อยู่ในรูปของค่าสัมบูรณ์ การแก้สมการค่าสัมบูรณ์จะคล้ายๆกับการแก้อสมการตัวแปรเดียว นั่นคือ คำตอบของสมการมีคำตอบได้หลายค่า ความแตกต่างก็คือ การแก้อสมการค่าสัมบูรณ์ต้องใช้สมบัติของค่าสัมบูรณ์มาช่วยด้วย

สามารถอ่านบทความเรื่องค่าสัมบูรณ์ได้ที่ >>>ค่าสัมบูรณ์<<<

ทฤษฎีบทที่ควรรู้เกี่ยวกับ อสมการค่าสัมบูรณ์

ให้ a และ b เป็นจำนวนจริงใดๆ และ c ≥ 0

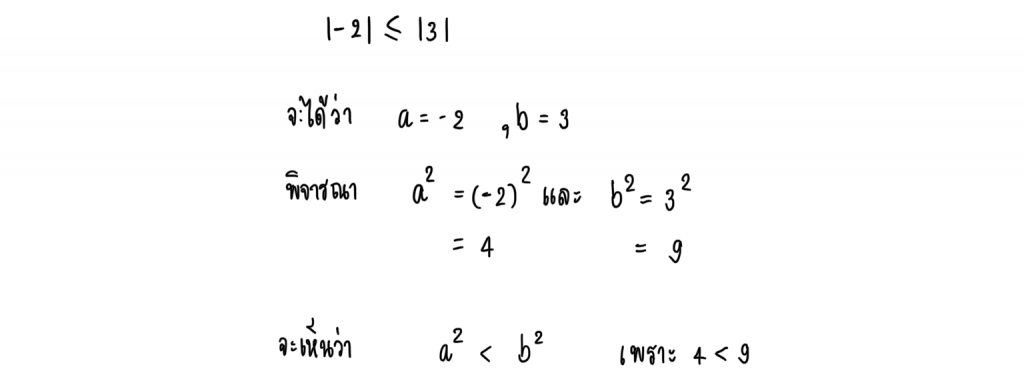
1.) $อสมการค่าสัมบูรณ์$ ก็ต่อเมื่อ $a^{2}< b^{2}$

ที่มา

2.) $\left | a \right |\leq \left | b \right |$ ก็ต่อเมื่อ $a^{2} \leq b^{2}$

เช่น

$\left | -2 \right | \leq \left | 3 \right |$

3.) $\left | a \right |< c$ ก็ต่อเมื่อ $-c< a< c$

ที่มาของทฤษฎีบท

เช่น $\left | x \right | < 3$ จะได้ว่า $-3< x< 3$

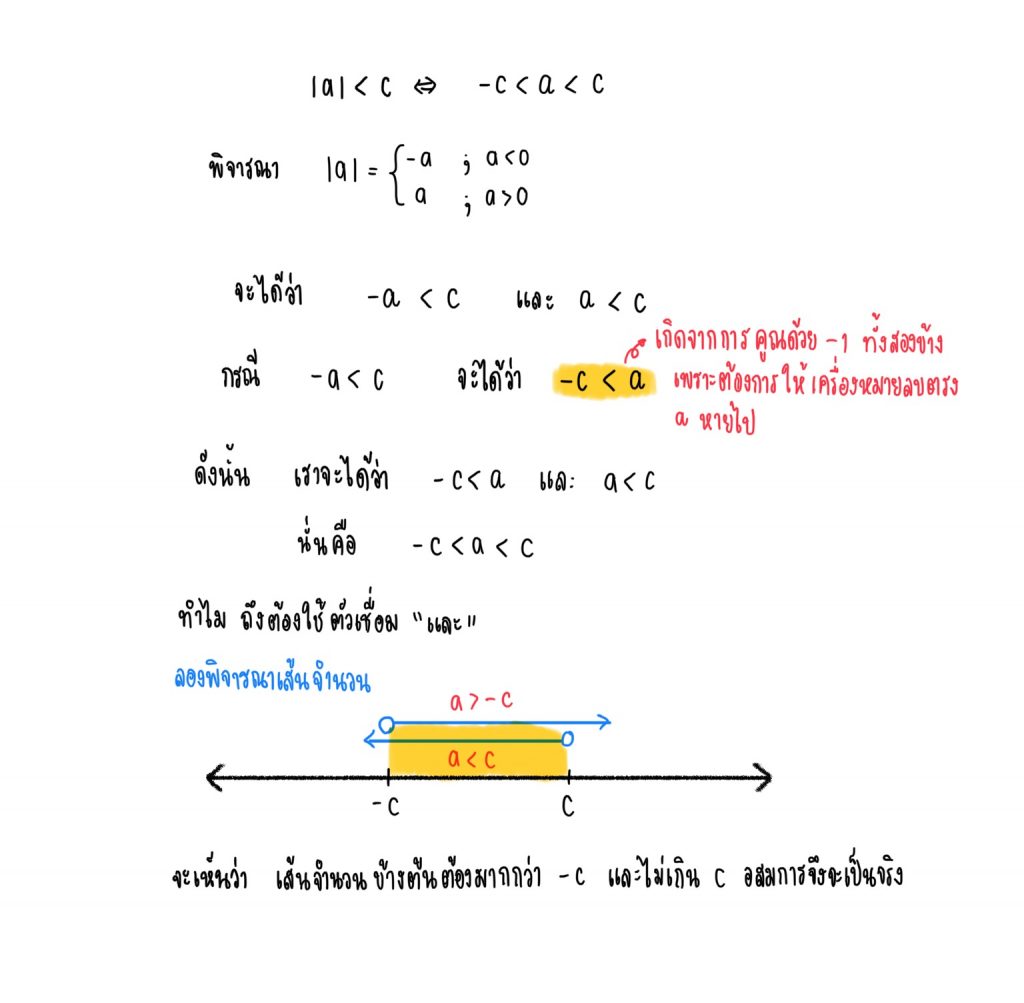
4.) $อสมการค่าสัมบูรณ์$ ก็ต่อเมื่อ $อสมการค่าสัมบูรณ์$

ที่มาคล้ายกับข้อ 3 แค่เปลี่ยนเป็นเครื่องหมายมากกว่าหรือเท่ากับแค่นั้นจ้า

5.) $อสมการค่าสัมบูรณ์$ ก็ต่อเมื่อ $a> c$ หรือ $a<-c$

ที่มาของทฤษฎีบท

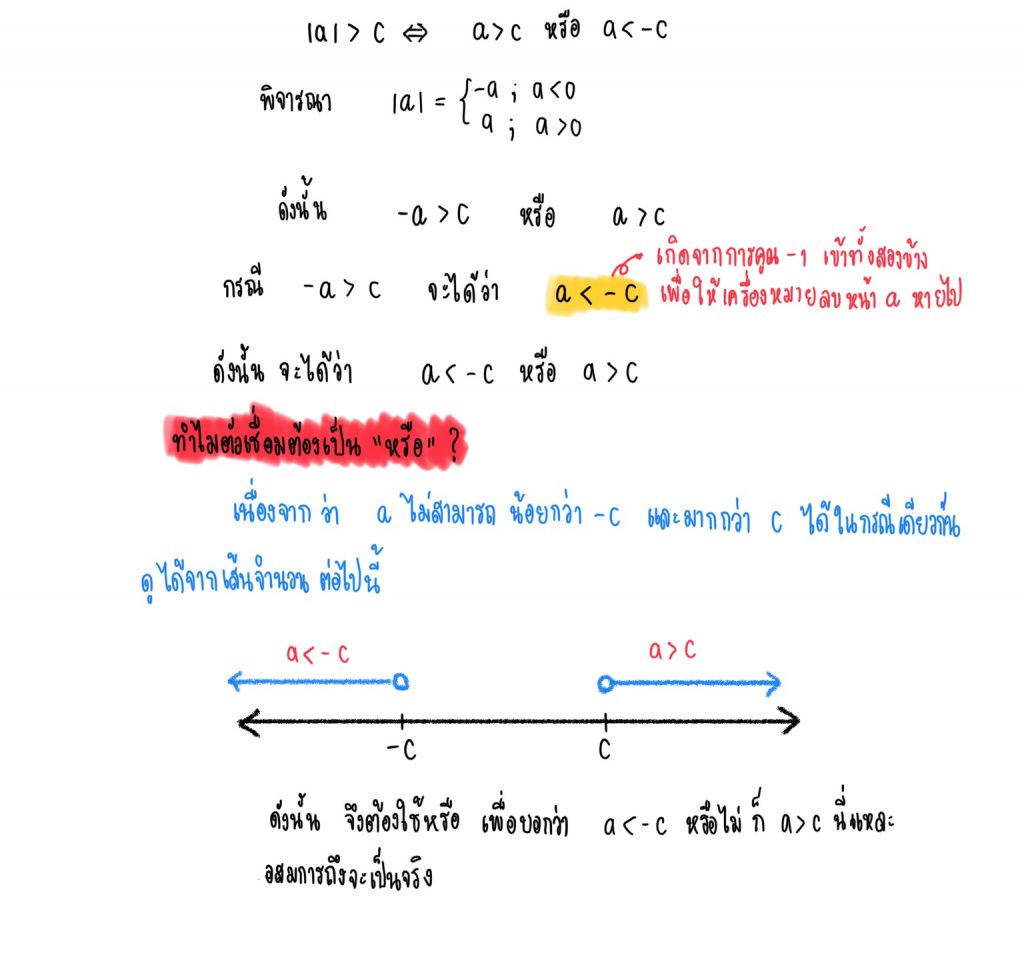
6.) $อสมการค่าสัมบูรณ์$ ก็ต่อเมื่อ $a\geq c$ หรือ $a\leq -c$

ตัวอย่างอสมการค่าสัมบูรณ์

1.) จงแก้อสมการ $\left |x-2 \right |< 5$

2.) จงแก้อสมการ $\left | 2-7m \right |-1> 4$

3.) เขียนข้อความต่อไปนี้ให้อยู่ในรูปของอสมการค่าสัมบูรณ์

3.1) s อยู่ห่างจาก 1 อย่างน้อย 4 หน่วย

วิธีทำ

เขียนเส้นจำนวนได้ดังนี้

s อยู่ห่างจาก 1 สามารถแปลได้อีกแบบคือ ผลต่างระหว่าง s กับ 1 มีค่าอย่างน้อย 4 หน่วย

อย่างน้อย 4 หน่วย หมายความว่า อาจจะลบกันแล้ว ได้ 4, 5, 6 หรืออาจจะมากกว่านี้ แสดงว่า ผลต่างของ s กับ 1 มีค่ามากกว่าหรือเท่ากับ 4 นั่นเอง

เขียนเป็นอสมการค่าสัมบูรณ์ได้ ดังนี้ $\left | s-1 \right |\geq 4$

3.2) k อยู่ห่างจาก 5 ในระยะ 2 หน่วย

วิธีทำ k อยู่ห่างจาก 5 ในระยะไม่เกิน 2 หน่วย เขียนบนเส้นจำนวนได้ดังนี้

จาก ระยะห่างระหว่าง k กับ 5มีค่าไม่เกิน 2 หน่วย หมายความว่า ผลต่างของ k กับ 5 มีค่าได้มากสุดคือ 2

ดังนั้น เขียนเป็นอสมการค่าสัมบูรณ์ได้ ดังนี้ $\left | k-5 \right |\leq 2$

ทำไมถึงต้องติดค่าสัมบูรณ์ อย่าลืมว่าโจทย์นั้นพูดถึงระยะห่างบนเส้นจำนวน ซึ่งระยะต้องมีค่าเป็นบวกเสมอจึงต้องใส่ค่าสัมบูรณ์ไปด้วย

4.) จงหาค่า x เมื่อ 6 บวกด้วย 4 เท่าของ x แล้วค่าสัมบูรณ์ของผลรวมนั้นมีค่าไม่มากกว่า 1

วิธีทำ เงื่อนไขคือ ค่าสัมบูรณ์ของ 6 บวกด้วย 4เท่าของx มีค่าไม่มากกว่า 1

6 บวกด้วย 4เท่าของ x เขียนได้ดังนี้ 6 + 4x

มีค่าไม่มากกว่า 1 หมายความกว่า ต้องน้อยกว่าหรือเท่ากับ 1

ดังนั้นเราจะได้อสมการค่าสัมบูรณ์ คือ $\left | 6-4x \right |\leq 1$

แก้สมการหาค่า x จะได้

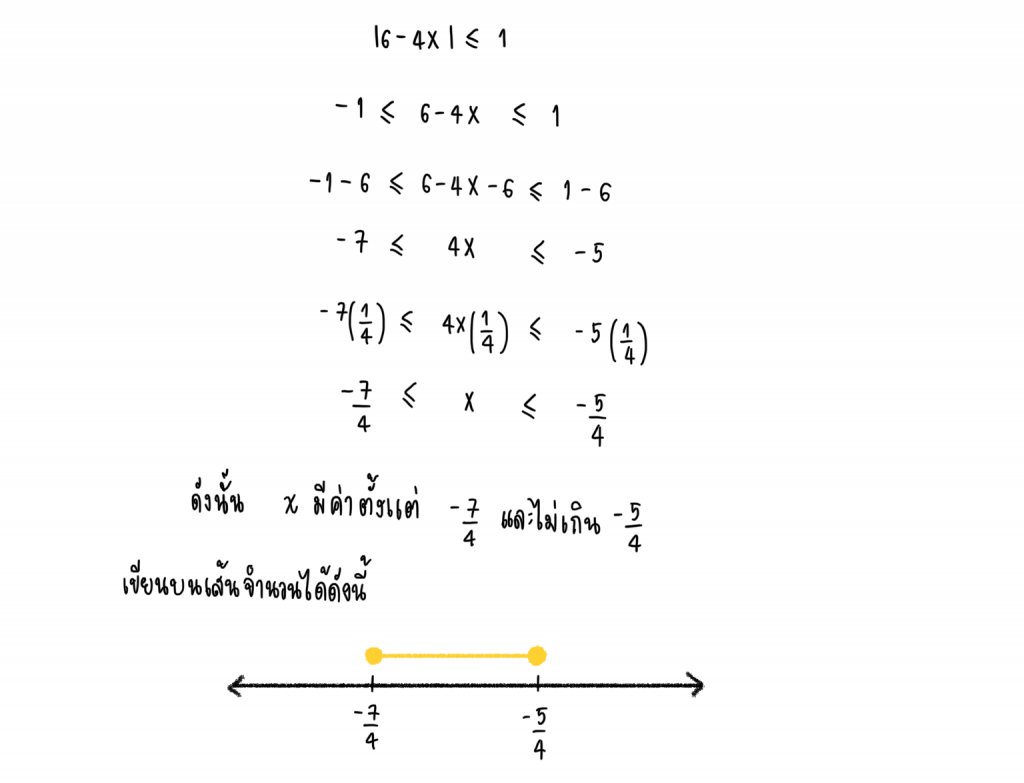
วิดีโอเกี่ยวกับการแก้อสมการค่าสัมบูรณ์

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

เรียนรู้และเข้าใจเรื่องคำซ้อนในภาษาไทย

คำซ้อน เป็นหนึ่งในบทเรียนหลักภาษาไทยเรื่องการสร้างคำ น้อง ๆ หลายคนอาจจะเคยสับสนกับวิธีสร้างคำซ้อน ไม่รู้ว่าแบบไหนกันแน่ที่เรียกว่าคำซ้อน เพราะภาษาไทยเรานั้นก็มีคำมากมายเหลือเกิน วันนี้เราจะมาเรียนรู้เรื่องคำซ้อนให้มากขึ้น รับรองว่าไม่ยากแน่นอนค่ะ คำซ้อน ความหมายของคำซ้อน คำซ้อน คือ คำที่เกิดจากการนำคำตั้งแต่ 2 คำ ขึ้นไปมาเรียงต่อกัน โดยคำที่นำมาซ้อนกันจะต้องเป็นคำที่มีความหมายเหมือนกัน ใกล้เคียงกัน ตรงข้ามกัน หรืออาจมีเสียงที่คล้ายกัน

การให้เหตุผลแบบอุปนัย

การให้เหตุผลแบบอุปนัย การให้เหตุผลแบบอุปนัย คือ การนำประสบการณ์มาสรุปผล เช่น เราไปซื้อผลไม้แล้วเราชิมผลไม้ 2-3 ลูก ปรากฏว่า มีรสหวาน เราเลยสรุปว่าผลไม้ทั้งกองนั้นหวาน เป็นต้น ซึ่งการสรุปผลอาจจะเป็นจริงหรือเท็จก็ได้ อาจจะขึ้นอยู่กับประสบการณ์ของผู้สรุป ดังนั้น ผลสรุปไม่จำเป็นต้องเหมือนกัน ตัวอย่างเช่น เหตุ เมื่อวานแป้งตั้งใจเรียน วันนี้แป้งตั้วใจเรียน ผลสรุป พรุ่งนี้แป้งจะตั้งใจเรียน การให้เหตุผลแบบนี้ เหมือนเป็นการคาดคะเนเหตุการณ์ที่จะเกิดขึ้นต่อไป ซึ่งการคาดคะเนนี้อาจจะจริงหรือเท็จก็ได้

Past Time หรือ เวลาในอดีต

สวัสดีค่ะนักเรียน ม.1 ที่น่ารักทุกคน วันนี้ครูจะพาไปดูเทคนิคและวิธีการใช้ Past Time หรือ เวลาในอดีต ซึ่งเมื่อเล่าถึงเวลาในอดีตส่วนใหญ่แล้วเรามักเจอคำว่า yesterday (เมื่อวานนี้), 1998 (ปี ค.ศ. ที่ผ่านมานานแล้ว), last month (เดือนที่แล้ว) และกลุ่มคำอื่นๆ ที่กำกับเวลาในอดีต ซึ่งเราจะเจอ Past Time ในกลุ่ม Past

ป.6 Possessive pronoun โดยใช้ Whose_ Which ร่วมด้วย

การใช้ Possessive pronoun โดยใช้ Whose/ Which ร่วมด้วย

สวัสดีค่ะนักเรียนชั้นป.6 ที่น่ารักทุกคนค่ะ วันนี้เราจะไปเรียนรู้เรื่อง การใช้ Possessive pronoun โดยใช้ Whose/ Which ร่วมด้วย Let’s go! ไปลุยกันเลยจ้า Possessive pronoun คืออะไร What’s mine is yours, my dear.