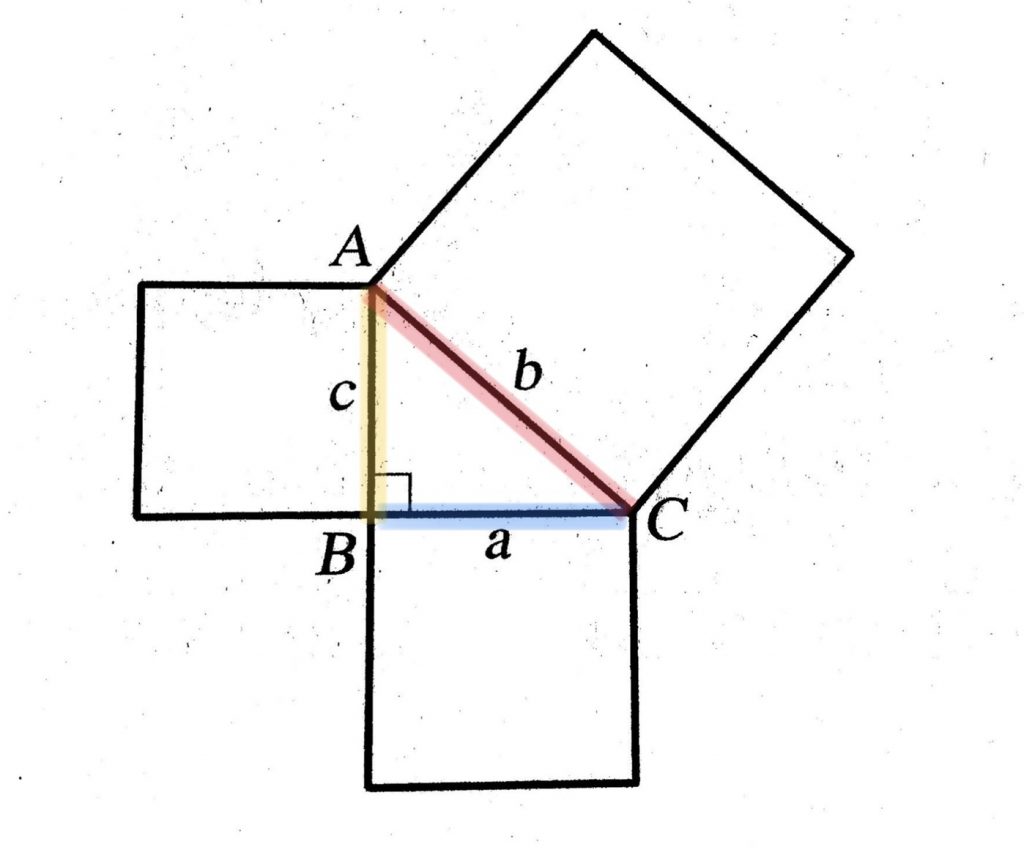
ในชีวิตประจำวันของเราเกี่ยวข้องกับรูปเรขาคณิตเสมอ เราใช้สมบัติของรูปเรขาคณิตในงานก่อสร้าง เช่นใช้สมบัติของรูปสามเหลี่ยมในการประกอบโครงของบ้านหรืออาคาร โดยใช้มุมฉากในการตั้งเสาบ้านให้ตั้งฉากกับพื้นดินเพื่อให้บ้านแข็งแรงและรับน้ำหนักได้ดี หรือสร้างไม้ค้ำประกอบเป็นรูปสามเหลี่ยมมุมฉากค้ำชายคาบ้านให้แข็งแรงมั่นคง
สมบัติของรูปสามเหลี่ยมมุมฉาก
พิจารณารูปสามเหลี่ยมมุมฉาก ABC ที่มี B เป็นมุมฉาก
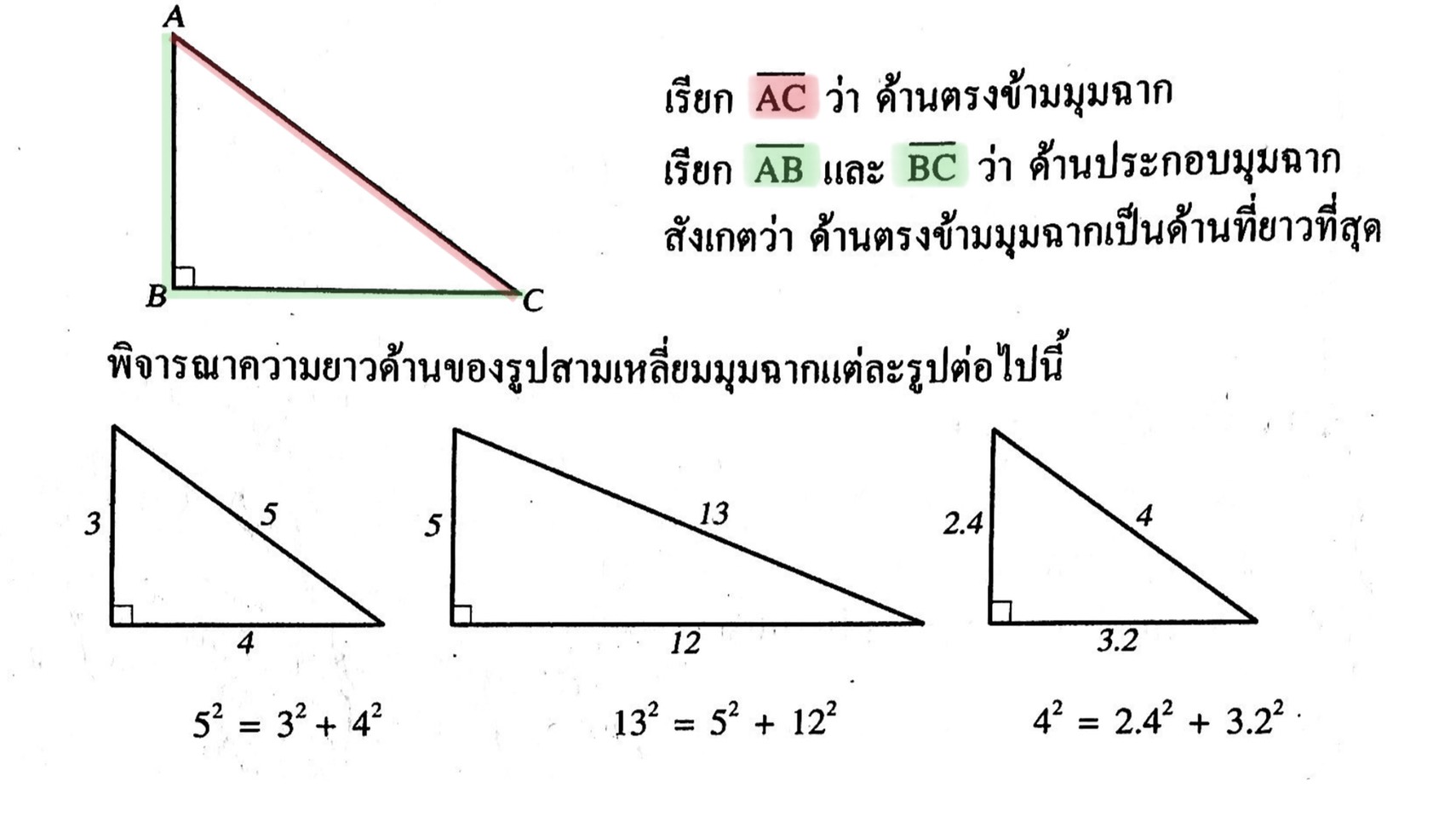
ความสัมพันธ์ระหว่างความยาวของด้านทั้งสามของรูปสามเหลี่ยมมุมฉากข้างต้นเป็นไปตามสมบัติของรูปสามเหลี่ยมมุมฉากที่กล่าวว่า
“สำหรับรูปสามเหลี่ยมมุมฉากใดๆ กำลังสองของความยาวของด้านตรงข้ามมุมฉากเท่ากับผลบวกของกำลังสองของความยาวของด้านประกอบมุมฉาก”
ซึ่งสมบัติข้างต้นนี้เรียกว่า ทฤษฎีบทพีทาโกรัส และเชื่อว่านักคณิตศาสตร์ชาวกรีกชื่อพีทาโกรัสเป็นผู้พิสูจน์ได้เป็นคนแรก
นั่นคือ รูปสามเหลี่ยมมุมฉาก ABC ใด ๆ ที่มี B เป็นมุมฉาก ถ้ากำหนดให้ b แทนความยาวของด้านตรงข้ามมุมฉาก a และ c แทนความยาวของด้านประกอบมุมฉาก ดังรูป

ตัวอย่างที่ 1
จากรูปสี่เหลี่ยมมุมฉากที่กำหนดให้ในแต่ละข้อต่อไปนี้ ให้เขียนความสัมพันธ์ระหว่างด้านทั้งสาม
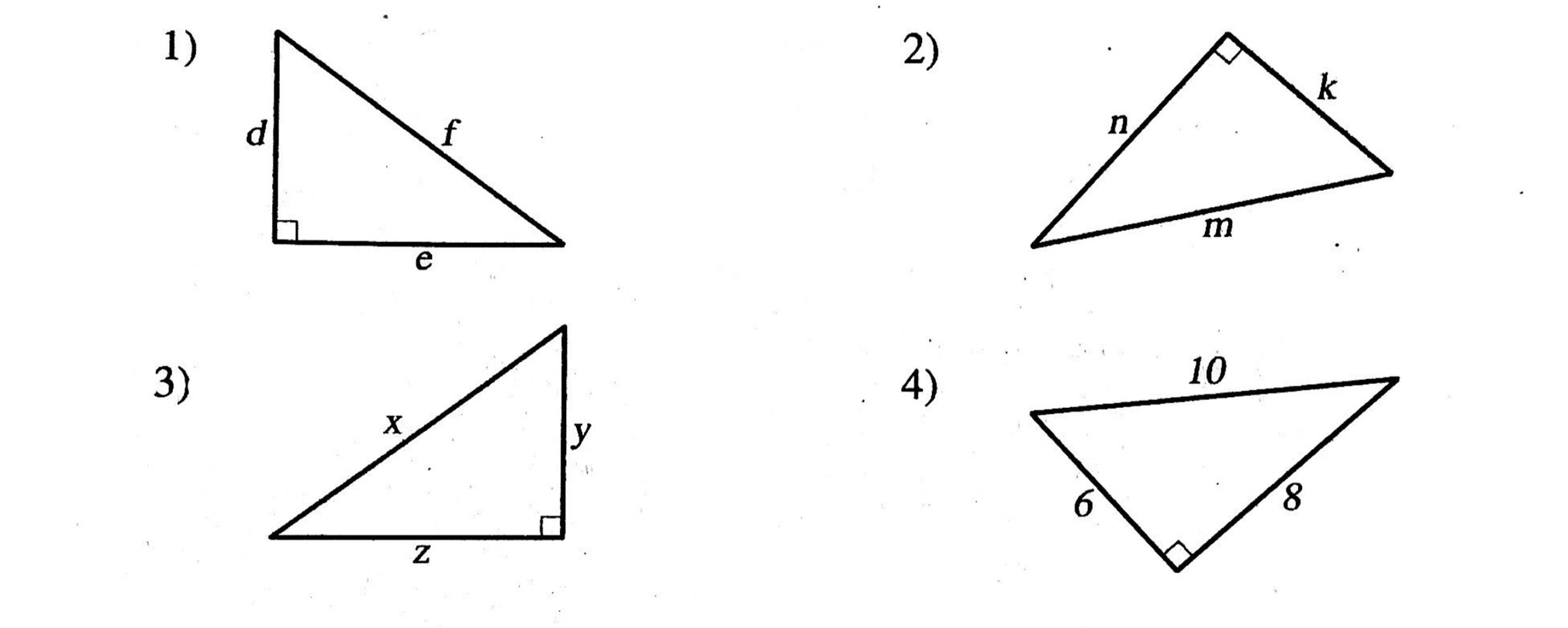
วิธีทำ จากรูปในแต่ละข้อสามารถเขียนความสัมพันธ์ของด้านทั้งสามได้ดังนี้
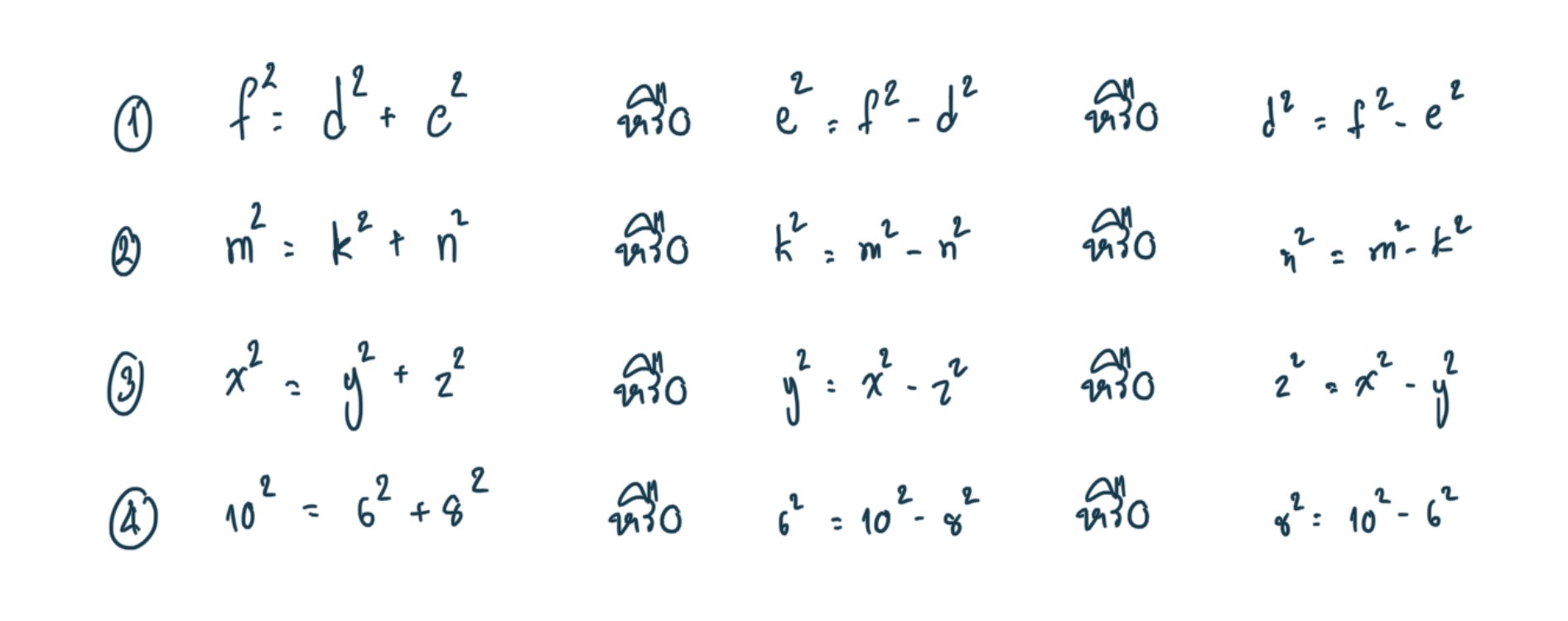
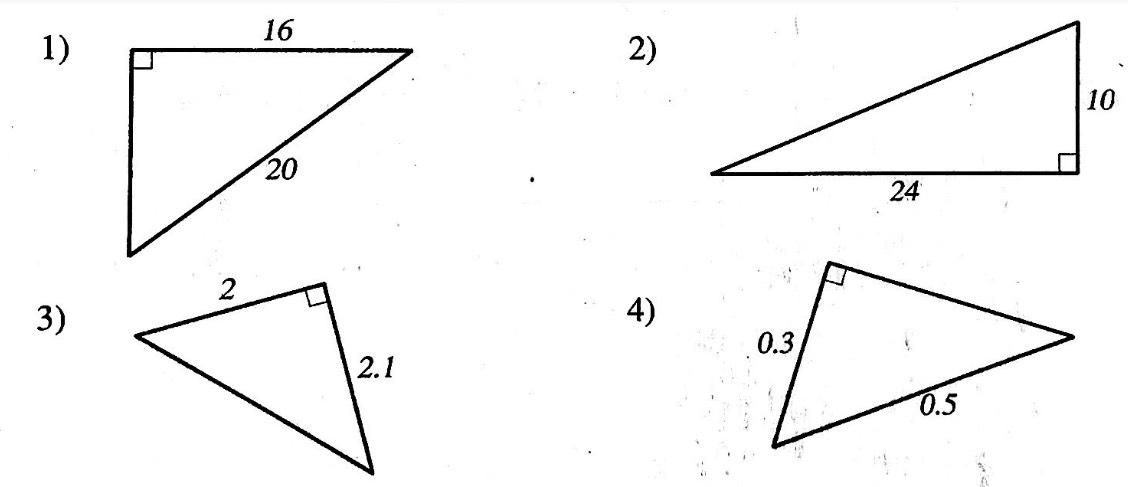
ตัวอย่างที่ 2 จากรูปที่กำหนดให้ในแต่ละข้อต่อไปนี้ จงหาความยาวของด้านที่เหลือ

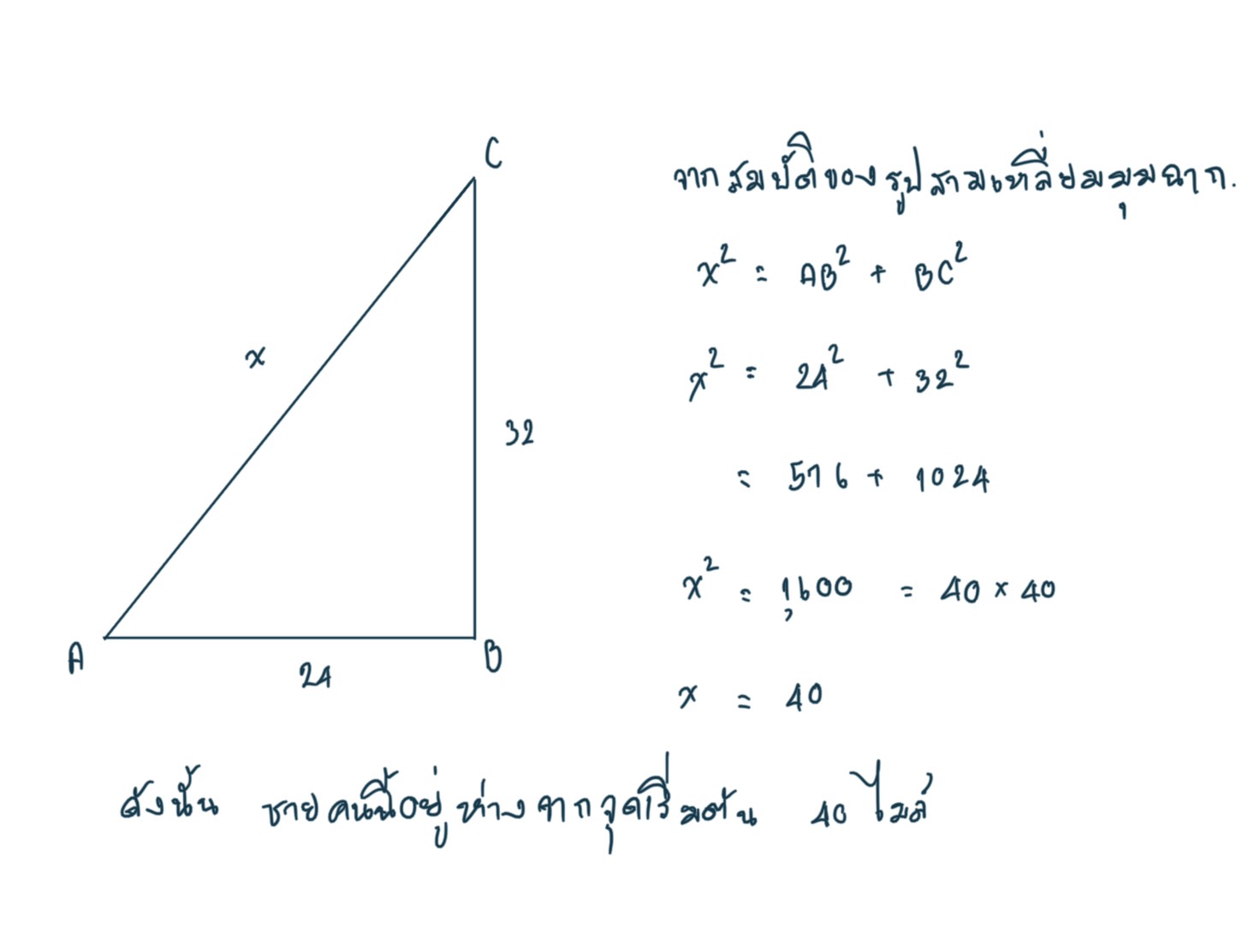
ตัวอย่างที่ 3 ชายคนหนึ่งเดินทางไปทิศตะวันออกได้ 24 ไมล์ แล้วเดินทางเลี้ยวไปทางทิศเหนืออีก 32 ไมล์ อยากทราบว่าชายคนนี้อยู่ห่างจากจุดเดิมไมล์
วิธีทำ เขียนแผนผังการเดินทางของชายคนหนึ่งโดยเริ่มที่จุด A สมมติให้ชายคนนั้นอยู่ห่าง x ไมล์