รากที่สอง

การหารากที่สองของจำนวนจริงทำได้หลายวิธี สำหรับวิธีการคำนวณ นักเรียนจะได้เรียนในระดับชั้นที่สูงกว่านี้ สำหรับในชั้นนี้ นักเรียนอาจใช้การแยกตัวประกอบ การประมาณ การเปิดตาราง

tucksaga

คณิตศาสตร์, คณิตศาสตร์ ม.2, ม.2, รากที่สอง ม.2

Add LINE friends for one click to find article.

วิธีการถอดกรณฑ์หรือรากที่สองนั้นไม่ได้ยากเหมือนหน้าตาของมันเลย การจะถอดรากที่สองนั้นคุณแค่ต้องแยกตัวประกอบตัวเลขแล้วดึงรากของจำนวนกำลังสองสมบูรณ์ใดๆ ที่หาได้ในเครื่องหมายกรณฑ์นั้น พอคุณเริ่มจำจำนวนกำลังสองสมบูรณ์ที่พบบ่อยไม่กี่ตัวนั้นได้และรู้วิธีแยกตัวประกอบของตัวเลขแล้ว คุณก็กำลังอยู่ในเส้นทางที่จะถอดรากที่สองได้แล้ว

นิยามของรากที่สอง

ให้ a แทนจำนวนจริงบวกใด ๆ หรือศูนย์ รากที่สองของ a คือจำนวนจริงที่ยกกำลังสองแล้วได้ a

สำหรับรากที่สองของจำนวนจริงลบจะไม่กล่าวถึง ณ ที่นี้เพราะไม่มีจำนวนจริงใดที่ยกกำลังสองแล้วได้จำนวนจริงลบ แต่จะกล่าวถึงในการเรียนขั้นสูงต่อไป

ตัวอย่างของรากที่สอง

-7 เป็นรากที่สองของ 49 เพราะ (-7)² = 49

10 เป็นรากที่สองของ 100 เพราะ 10² = 100

25 เป็นรากที่สองของ 625 เพราะ 25² = 625

-25 เป็นรากที่สองของ 625 เพราะ (-25) = 625

ดังนั้นถ้า a เป็นจำนวนจริงบวก รากที่สองของ a มี 2 ราก คือรากที่สองที่เป็นบวก และรากที่สองที่เป็นลบ

และถ้า a = 0 รากที่สองของ a คือ 0

จากตัวอย่างทั้งสามข้อจะเห็นว่า รากที่สองของบางจำนวนเป็นจำนวนตรรกยะ และรากที่สองของบางจำนวนเป็นจำนวนอตรรกยะ

การหาค่ารากที่สองของจำนวนจริงบวกใด ๆ การจัดให้อยู่ในรูปกำลังสองจะทำให้หาผลลัพธ์ได้รวดเร็วดังนั้นจึงนิยมจัดรูปเป็นกำลังสอง แต่เนื่องจากจำนวนที่ยกกำลังแล้วได้จำนวนจริงบวกที่ต้องการมีหลายจำนวนเช่น

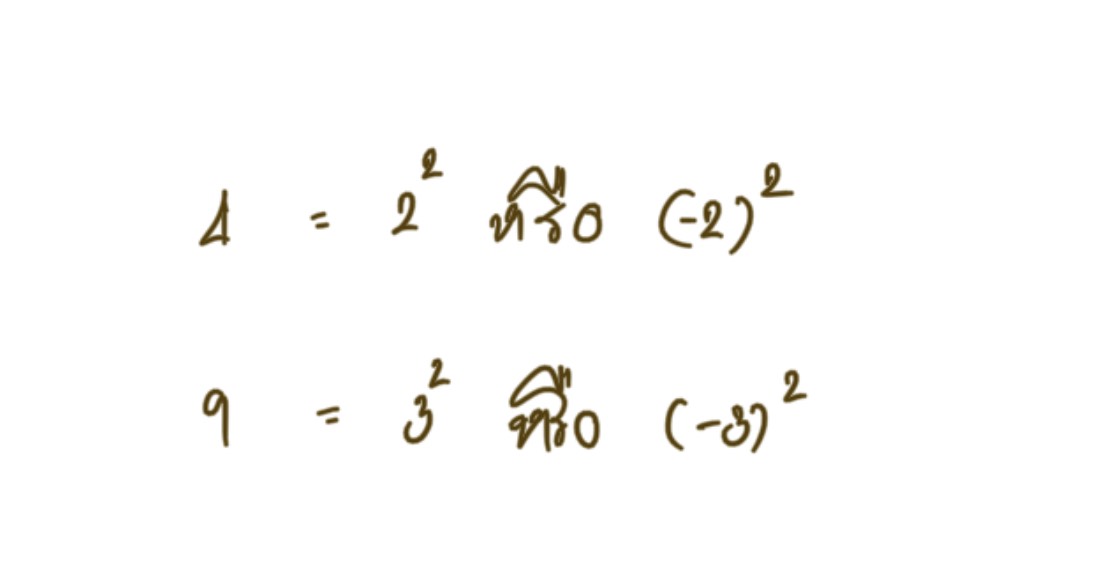
ดังนั้นเพื่อจัดอยู่ในรูปทั่วไปจึงกำหนดนิยามเพิ่มเติมต่อไปนี้

การหารากที่สองของจำนวนเต็มบวก

ถ้าสามารถหาจำนวนเต็มบวกจำนวนหนึ่งที่ยกกำลังสองแล้วเท่ากับจำนวนเต็มบวกที่กำหนดให้รากที่สองของจำนวนนั้นจะเป็นจำนวนตรรกยะที่เป็นจำนวนเต็ม
ถ้าไม่สามารถหาจำนวนเต็มบวกที่ยกกำลังสองแล้วเท่ากับจำนวนเต็มบวกที่กำหนดให้รากที่สองของจำนวนจะเป็นจำนวนอตรรกยะ

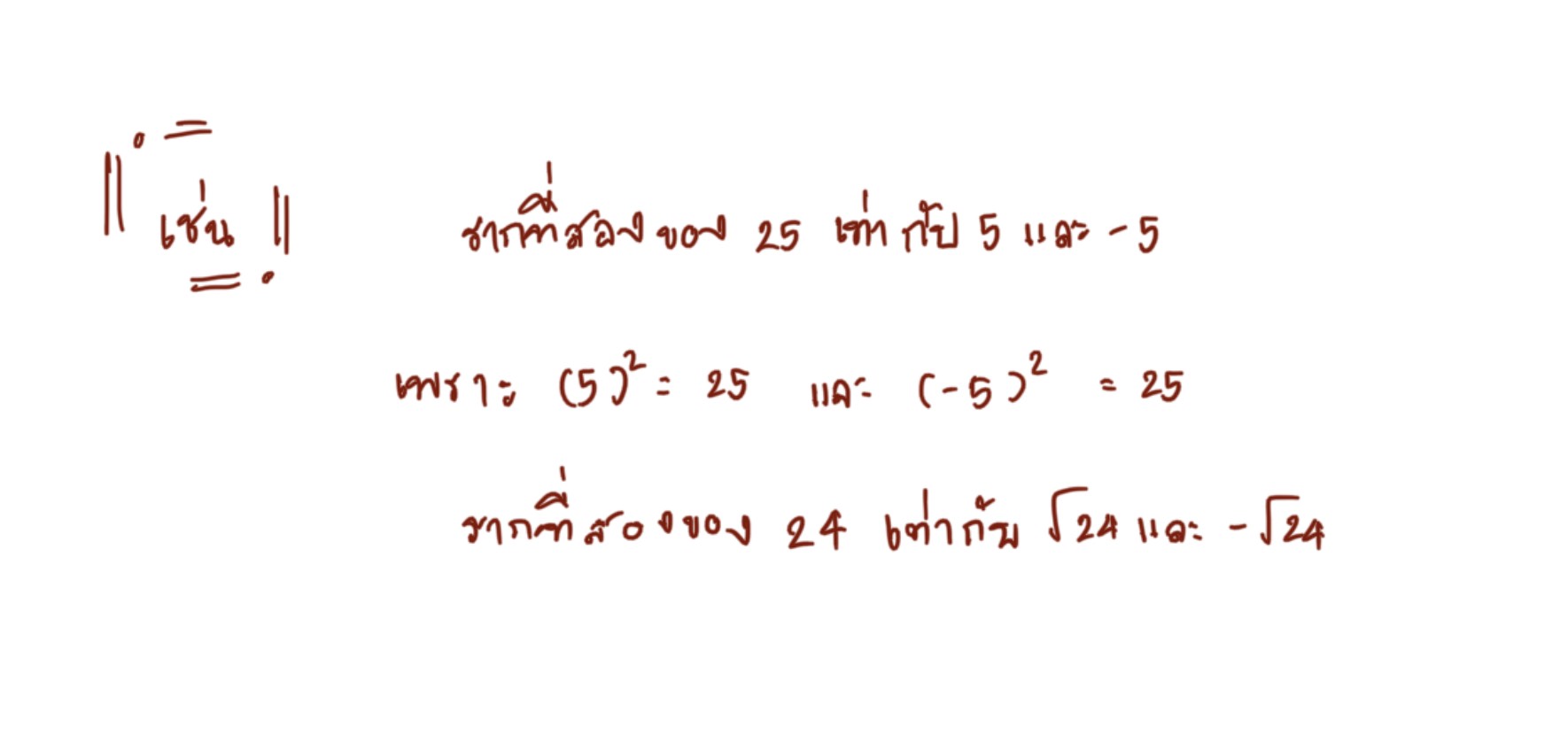
จำนวนตรรกยะอื่น ๆ ที่ไม่ใช่จำนวนเต็มพิจารณาดังนี้ถ้าสามารถหาจำนวนตรรกยะที่ยกกำลังสองแล้วเท่ากับจำนวนตรรกยะบวกที่กำหนดให้รากที่สองของจำนวนนั้นจะเป็นจำนวนตรรกยะ แต่ถ้าไม่สามารถหาจำนวนตรรกยะที่ยกกำลังสองแล้วเท่ากับจำนวนตรรกยะบวกที่กำหนดให้รากที่สองของจำนวนนั้นจะเป็นจำนวนอตรรกยะ

การหาค่าของรากที่สอง

1.การหาค่าของรากที่สองโดยวิธีการแยกตัวประกอบ ใช้สำหรับจำนวนจริงที่สามารถแจกตัวประกอบได้เป็นจำนวนตรรกยะ ซึ่งพิจารณาได้ดังตัวอย่างต่อไปนี้

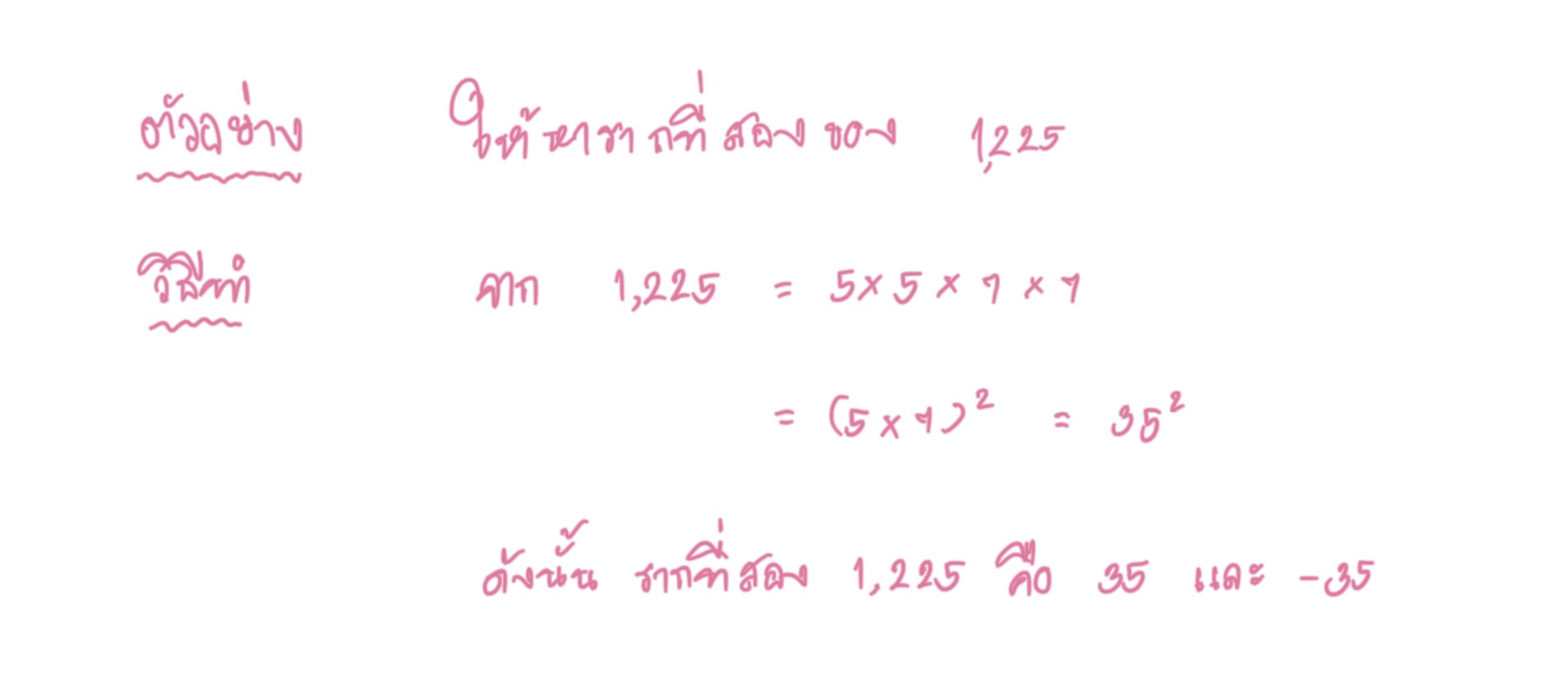
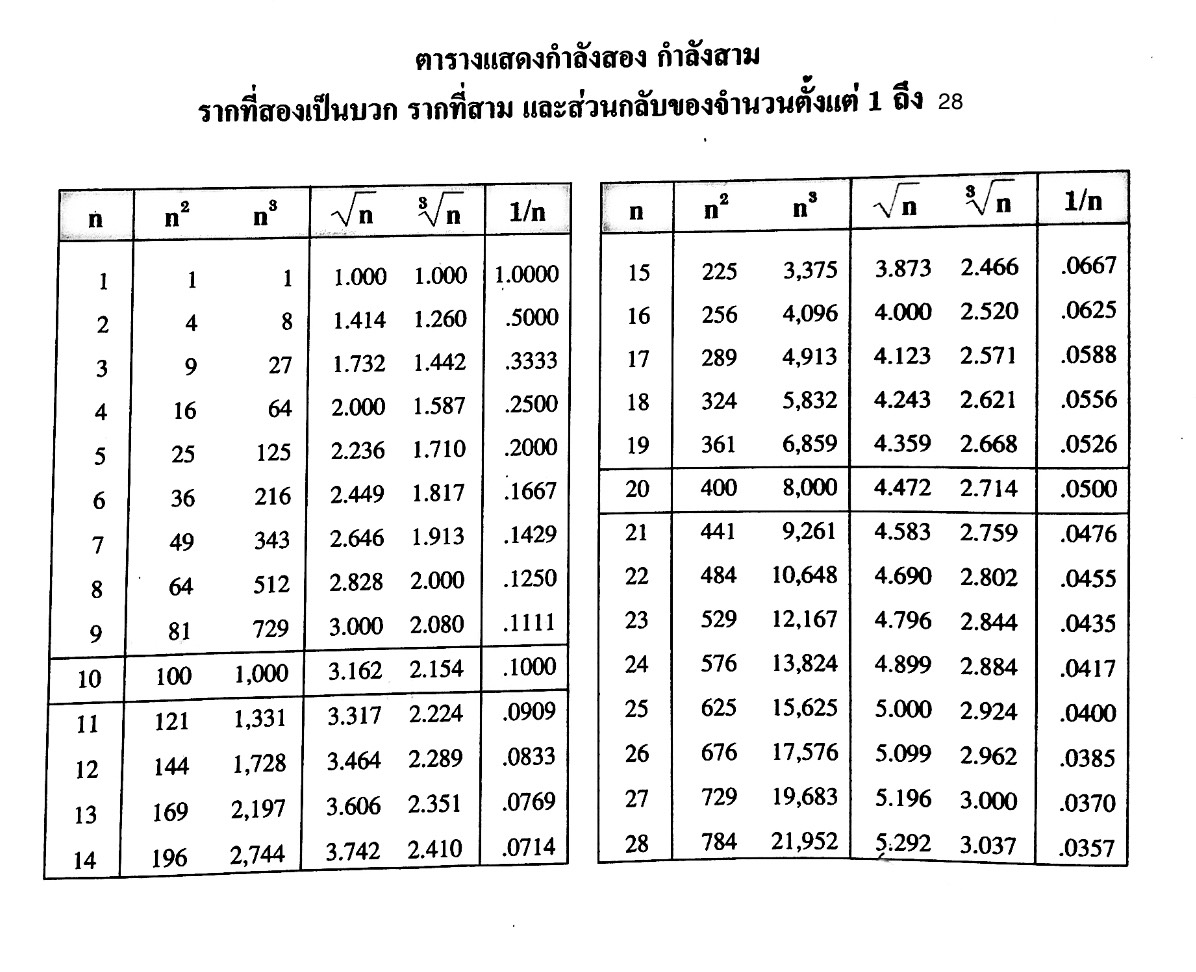
2. การหาค่าของรากที่สองจากตาราง ซึ่งตารางนี้มีผู้สร้างขึ้นเพื่อความสะดวกในการนำไปใช้ โดยตารางนี้เป็นการแสดงรากที่สองที่เป็นบวกของจำนวนเต็มบวก

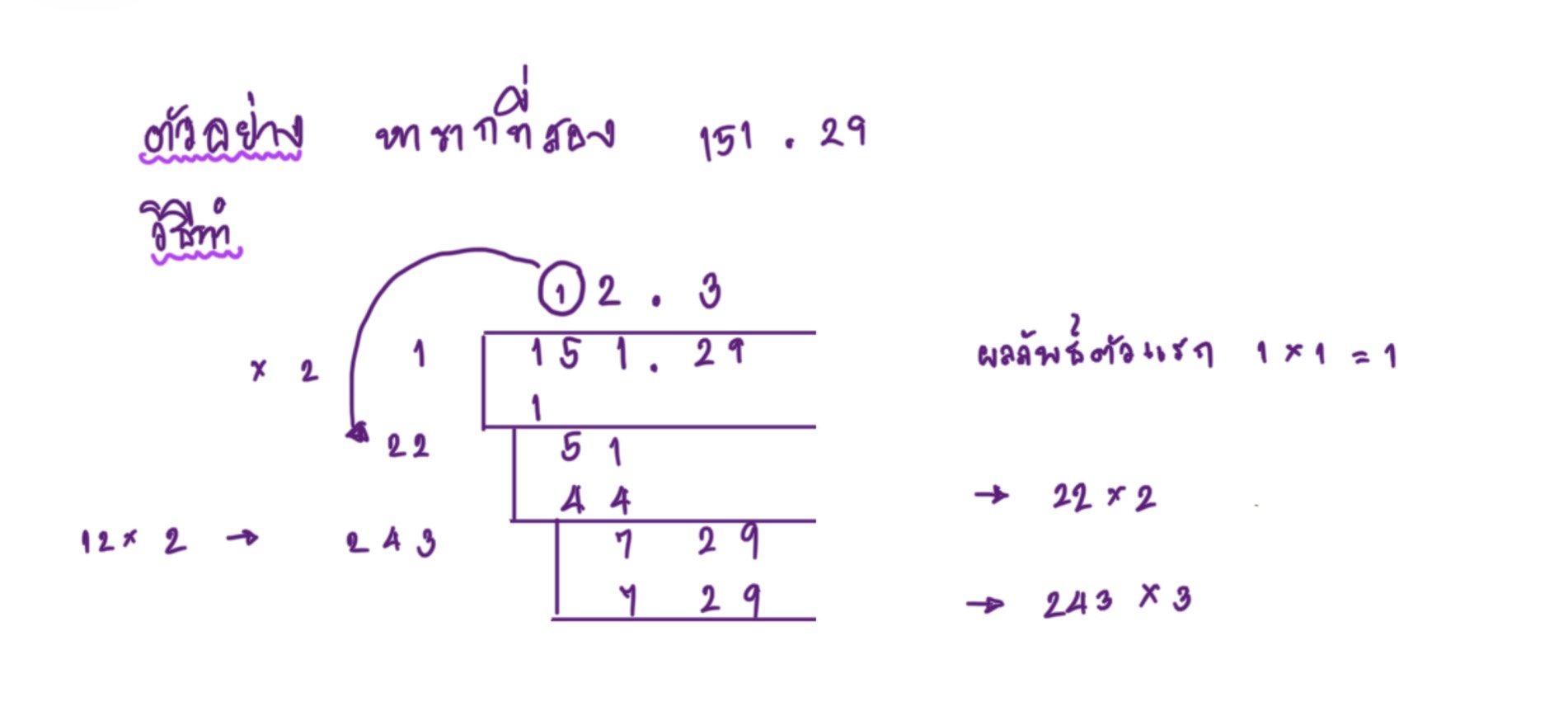
3.การหาค่ารากที่สองดดวิธีการตั้งหาร มีหลักการดังนี้

3.1 แบ่งจำนวนที่ต้องการหาค่ารากที่สองออกเป็นชุดๆ ชุดละ 2ตัว โดยตัวเลขหน้าจุดแบ่งจากขวามาซ้าย และเลขหลังจุดแบ่งจากซ้ายไปขวา เช่น

3.2 นำจำนวนที่ต้องการหารากที่สองมาหารยาว โดยมีวิธีการดังตัวอย่างต่อไปนี้

ตัวอย่างคลิปเรื่องรากที่สอง

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

$หลักการเบื้องต้นของอัตราส่วน$

หลักการเบื้องต้นของอัตราส่วน

“อัตราส่วน คือ ปริมาณ อย่างหนึ่งที่แสดงถึง จำนวน หรือ ขนาด ตามสัดส่วนเมื่อเปรียบเทียบกับอีก ปริมาณ หนึ่งที่เกี่ยวข้องกัน ที่อาจมีได้ตั้งแต่สองปริมาณขึ้นไป”

Modals in the Past

สวัสดีค่านักเรียนชั้นม.6 ที่น่ารักทุกคน วันนี้เราจะไปดู ” Modals in the Past “ ที่ใช้บ่อยพร้อมเทคนิคการใช้งานง่ายๆกันค่า Let’s go! ไปลุยกันเลยจร้า ทบทวน Modal Verbs Modal Auxiliaries คือ กริยาช่วยกลุ่ม Modal verbs หรือ

การหารเลขยกกำลัง เมื่อเลขชี้กำลังเป็นจำนวนเต็มบวก

การหารเลขยกกำลัง เมื่อเลขชี้กำลังเป็นจำนวนเต็มบวก บทความนี้ ได้รวบรวมตัวอย่าง การหารเลขยกกำลัง เมื่อเลขชี้กำลังเป็นจำนวนเต็มบวก ซึ่งทำได้โดยการใช้สมบัติการหารของเลขยกกำลัง ก่อนจะเรียนรู้ ตัวอย่างการหารเลขยกกำลัง เมื่อเลขชี้กำลังเป็นจำนวนเต็มบวก น้องๆจำเป็นต้องมีความรู้ในเรื่อง การคูณเลขยกกำลัง เมื่อเลขชี้กำลังเป็นจำนวนเต็มบวก สามารถศึกษาเพิ่มเติมได้ที่ ⇒⇒ การคูณเลขยกกำลัง เมื่อเลขชี้กำลังเป็นจำนวนเต็มบวก ⇐⇐ สมบัติของการหารเลขยกกำลัง am ÷ an = am – n (ถ้าเลขยกกำลังฐานเหมือนกันหารกัน ให้นำเลขชี้กำลังมาลบกัน)

โต้วาที และยอวาที แต่งต่างกันอย่างไร?

การพูดมีมากมายหลายประเภท แล้วแต่จุดประสงค์ของผู้พูดว่าต้องการจะสื่อสารออกมาในรูปแบบใด แต่จะมีอยู่ประเภทหนึ่งที่มีหัวข้อให้พูดและต้องแบ่งออกเป็นสองฝ่าย โดยไม่ได้มีเจตนาเพื่อมาทะเลาะกัน เพราะเรากำลังหมายถึงการพูดโต้วาทีและการยอวาที ที่เป็นการพูดแสดงความคิดเห็นในลักษะที่ต่างกัน แต่จะต่างกันอย่างไรบ้างนั้น เราไปเรียนรู้เรื่องนี้พร้อมกันเลยค่ะ การโต้วาที การโต้วาที เป็นการแสดงความคิดเห็นโต้แย้งด้วยเหตุผลเพื่อให้ชนะอีกฝ่าย โดยจะแบ่งผู้พูดออกเป็น 2 ฝ่าย คือ ฝ่ายญัตติและฝ่ายคัดค้านญัตติ และมีกรรมการคอยตัดสินว่าจะให้ฝ่ายใดชนะ โดยแต่ละฝ่ายจะต้องมีข้อมูลเพื่อมาสนับสนุนการพูดของตัวเอง หักล้างแนวคิดของอีกฝ่ายและต้องมีปฏิภาณไหวพริบ องค์ประกอบของการโต้วาที

ความน่าจะเป็นของเหตุการณ์

ความน่าจะเป็นของเหตุการณ์ บทความนี้ได้รวบรวมความรู้เรื่อง ความน่าจะเป็นของเหตุการณ์ ซึ่งได้กล่าวถึงขั้นตอนและวิธีการหาความน่าจะเป็นของเหตุการณ์ และยกตัวอย่างประกอบ อธิบายอย่างละเอียด ซึ่งก่อนจะเรียนเรื่อง ความน่าจะเป็นของเหตุการณ์น้องๆสามารถทบทวน การทดลองสุ่มและเหตุการณ์ ได้ที่ ⇒⇒ การทดลองสุ่มและเหตุการณ์ ⇐⇐ ความน่าจะเป็นของเหตุการณ์ (probability) คือ อัตราส่วนระหว่างจำนวนเหตุการณ์ที่สนใจ (n(E)) กับจำนวนแซมเปิลสเปซ (n(S)) ที่มีโอกาสเกิดขึ้นได้พร้อม ๆ กัน ใช้สัญลักษณ์ “P(E)” แทนความน่าจะเป็นของการเกิดเหตุการณ์ที่สนใจ โดยที่

การใช้ประโยคคำสั่ง คำขอร้อง และคำแนะนำง่ายๆ

สวัสดีค่ะนักเรียนชั้นป.5 ที่น่ารักทุกคน วันนี้ครูจะพาเรียนรู้เกี่ยวกับ การใช้ประโยคคำสั่ง คำขอร้อง และคำแนะนำง่ายๆ “Easy Imperative Sentences” กันนะคะ ถ้าพร้อมแล้วก็ไปลุยกันเลย รูปแบบและโครงสร้างประโยคคำสั่ง Imperative sentence Imperative sentence ในรูปแบบประโยคบอกเล่าจะ ใช้ Verb base form (V.1)