เมื่อนำจำนวนบางคู่มาลบกัน หารกัน แล้วกระทำไม่ได้ จึงคิดค้นหลักการจำนวนอตรรกยะ นี้ทำให้ปัญหาที่เกิดขึ้นหายไป เช่น ช่วยแก้ปัญหาการหาคำตอบของสมการ เป็นต้น หากสงสัยว่าตัวเลขที่ให้มาแทนจำนวนอตรรกยะหรือไม่ ก็ต้องลองแปลงตัวเลขนั้นให้อยู่ในรูปทศนิยม หากแปลงออกมาแล้วได้เป็นทศนิยมไม่ซ้ำ ก็สรุปได้ว่าเป็นจำนวนอตรรกยะ
จำนวนอตรรกยะ
นอกจากจำนวนเต็ม เศษส่วน และทศนิยมที่เรารู้จักและนำไปใช้ในชีวิตประจำวันอย่างแพร่หลาย แต่ก็ยังมีสถานการณ์บางอย่างที่ไม่สามารถใช้จำนวนดังกล่าวได้ เช่น
ตัวอย่างโจทย์ปัญหา รูปสี่เหลี่ยมจัตุรัสที่มีพื้นที่ 20 ตารางหน่วย จะมีด้านยาวด้านละเท่าไร
การหาความยาวของด้าน สมมติให้ยาวด้านละ X หน่วย
ดังนั้น X x X = 20
และจากการทดลองแทนคำหาจำนวนที่คูณกันได้ 20 ซึ่งพบว่าไม่มีจำนวนเต็ม เศษส่วนหรือทศนิยมซ้ำใดที่คูณกันแล้วได้ 20 จึงจำเป็นต้องหาจำนวนมาแทนจำนวนที่คูณกันได้ 20

สรุป จำนวนที่ไม่สามารถเขียนแทนได้ด้วยทศนิยมซ้ำหรือเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็ม ที่ b ไม่เท่ากับ 0 เรียกว่า จำนวนอตรรกยะ

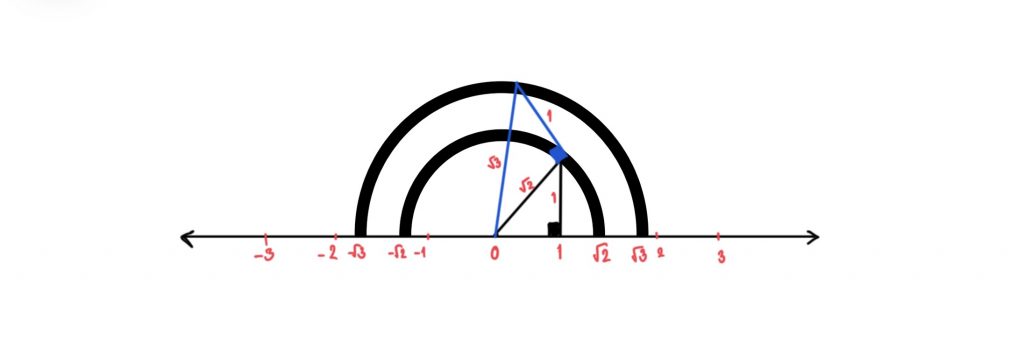
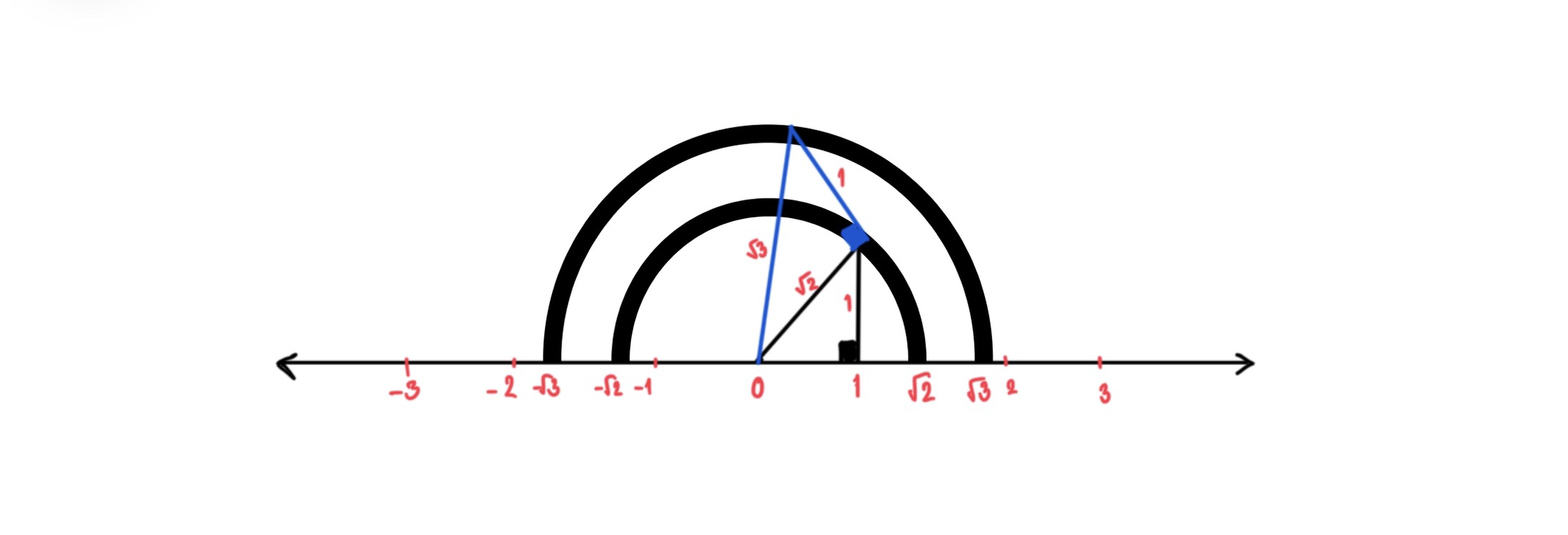
จำนวนตรรกยะจัดเป็นจำนวนจริง มีสมบัติการสลับที่ การเปลี่ยนหมู่ของการคูณและการบวก และมีสมบัติการแจกแจง เช่นเดียวกับจำนวนจริงอื่น ๆ และจำนวนจริงทุกจำนวนสามารถแทนได้ด้วยจุดบนเส้นจำนวนสำหรับจำนวนอตรรกยะก็สามารถแทนได้ด้วยจุดเป็นเส้นจำนวนเช่นกัน
ตัวอย่างการแทนจำนวนอตรรกยะด้วยจุดบนเส้นจำนวน
คลิปตัวอย่างเรื่องจำนวนอตรรกยะ