บทความนี้จะใช้เนื้อหาเรื่องการดำเนินการของเซตด้วยเล็กน้อย ก่อนอื่นเรามารู้จักกับ สัญลักษณ์ จำนวนของสมาชิกก่อนนะคะ
ให้A เป็นเซตจำกัด เราจะใช้ n(A) แทนจำนวนสมาชิกของเซต A
เช่น A = {a,b,c,d} จะได้ n(A) = 4
B = {5,6,7,8,9,10} จะได้ n(B) = 6
จำนวนสมาชิกของเซตจำกัดสองเซต
กรณีที่ 1 ถ้า A และ B เป็นเซตที่ไม่มีสมาชิกร่วมกัน
จะได้ว่า n(A∪B) = n(A)+n(B)
เช่น ให้ A = {1,2,3,4,5}, B = {6,7,8,9,10} จะได้ n(A) = 5, n(B) = 5
พิจารณา A∪B = {1,2,3,4,5,6,7,8,9,10} จะได้ n(A∪B) = 10
พิจารณา n(A)+n(B) = 5+5 = 10
ดังนั้นจะได้ว่า ถ้า A และ B ไม่มีสมาชิกร่วมกัน จะได้ n(A∪B) = n(A)+n(B)
กรณีที่ 2 ถ้า A และ B มีสมาชิกร่วมกัน
จะได้ว่า n(A∪B) = n(A)+n(B)-n(A∩B)
เช่น ให้ A ={1,2,3,4,5}, B = {4,5,6,7,8} จะได้ n(A) = 5 , n(B) = 5
พิจารณา A∪B = {1,2,3,4,5,5,6,7,8} จะได้ n(A∪B) = 8
พิจาณรา A∩B = {4,5} จะได้ n(A∩B) = 2
พิจารณา n(A)+n(B) = 5+5 = 10
พิจารณา n(A)+n(B)-n(A∩B) = 5+5-2 = 8
จะเห็นกว่า n(A∪B) ≠ n(A)+n(B) แต่ n(A∪B) = n(A)+n(B)-n(A∩B)
ดังนั้น ถ้า A,B มีสมาชิกร่วมกัน จะได้ว่า n(A∪B) = n(A)+n(B)-n(A∩B)
กรณีที่ 3 ถ้า A และ B เป็นเซตจำกัด จะได้ว่า n(A-B) = n(A) – n(A∩B)
จำนวนสมาชิกของเซตจำกัดสามเซต
ให้ A = {3,4,5,6} , B = {4,5,6,7}, C = {4,5,9}

ถ้าให้ A และ B เป็นเซตจำกัด
จะได้ว่า n(A-B-C) = n(A)-n(A∩B)-n(A∩C)+n(A∩B∩C)
สรุปสูตรการหาจำนวนสมาชิกของเซตจำกัด
ถ้า A, B และ C เป็นเซตจำกัด
1.) n(A∪B) = n(A)+n(B)-n(A∩B)
2.) n(A-B) = n(A) – n(A∩B)
3.) n(A∪B∪C) = n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩B∩C)
4.) n(A-B-C) = n(A)-n(A∩B)-n(A∩C)+n(A∩B∩C)
ตัวอย่าง
1.) ถ้า A และ B มีจำนวนสมาชิกเท่ากัน A∪B มีสมาชิก 15 ตัว และ A∩B มีสมาชิก 5 ตัว จงหาจำนวนสมาชิกของ A-B และ B-A
วิธีทำ จากโจทย์ n(A∪B) = 15 และ n(A∩B) = 5
จากสูตร n(A∪B) = n(A)+n(B)-n(A∩B)
จะได้ว่า 15 = n(A)+n(B)-5
บวก 5 เข้าทั้งสองข้างของสมการ จะได้
20 = n(A)+n(B)
จากที่เรารู้ว่า A และ B มีจำนวนสมาชิกเท่ากัน ทำให้ได้ว่า
n(A) = n(B) ดังนั้น เราจะแทน n(A) = n(B) ในสมการ 20 = n(A)+n(B)
จะได้ว่า 20 = n(A)+n(A)
20 = 2n(A)
หารด้วย 2 ทั้งสมการ จะได้
n(A) = 10 ทำให้ได้ว่า n(B) = 10
แต่โจทย์อยากได้ n(A-B) และ n(B-A)
จาก n(A-B) = n(A) – n(A∩B)
จะได้ว่า n(A-B) = 10-5 = 5
และ n(B-A) = n(B)-n(A∩B) = 10-5 = 5
ตอบ จำนวนสมาชิกของ A-B และ B-A เท่ากับ 5
เราสามารถหาคำตอบโดยการใช้แผนภาพได้ ดังนี้
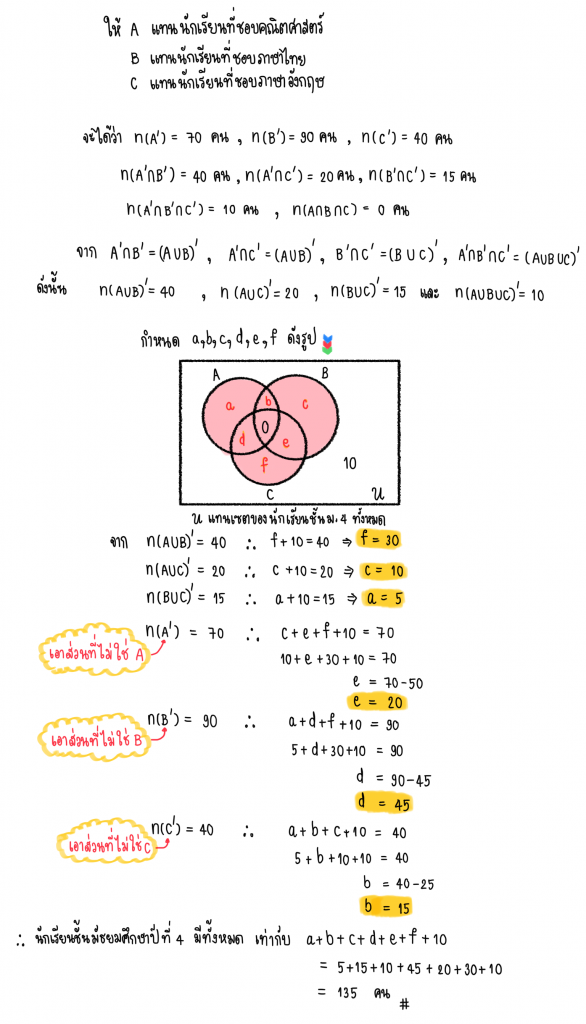
2.) จากผลสำรวจความชอบเกี่ยวกับวิชาคณิตศาสตร์ ภาษาไทย และอังกฤษของนักเรียนชั้นมัธยมศึกษาปีที่ 4 ทั้งหมด ผลเป็นดังนี้
ไม่ชอบคณิตศาสตร์ 70 คน
ไม่ชอบภาษาไทย 90 คน
ไม่ชอบอังกฤษ 40 คน
ไม่ชอบคณิตศาสตร์และไม่ชอบภาษาไทย 40 คน
ไม่ชอบคณิตศาสตร์และอังกฤษ 20 คน
ไม่ชอบภาษาไทยและอังกฤษ 15 คน
ไม่ชอบทั้งสามวิชา 10 คน
ชอบทั้งสามวิชาวิชา 0 คน
อยากทราบว่า มีนักเรียนชั้นมัธยมศึกษาปีที่ 4 ทั้งหมดกี่คน
วิธีทำ