ทบทวนจำนวนเต็ม
บทความนี้จะทำให้น้องๆ เข้าใจ การเปรียบเทียบจำนวนเต็ม ซึ่งได้รวบรวมตัวอย่างไว้อย่างหลากหลาย น้องๆรู้จัก จำนวนเต็ม กันแล้ว แต่หลายคนยังไม่สามาถเปรียบเทียบความมากน้อยของจำนวนเต็มเหล่านั้นได้ ซึ่งถ้าน้องๆ เคยเรียนเรื่องการเปรียบเทียบเศษส่วนและจำนวนคละมาแล้ว เรื่องนี้จะกลายเป็นเรื่องง่ายดาย ซึ่งได้นำเสนออกมาในรูปแบที่เข้าใจง่าย ทำให้น้องๆสนุกกับการเรียนคณิตศาสตร์
ทบทวนเรื่องจำนวนเต็ม เช่น
25 , 9 , -5 , 5.5 , 2.0 , 9.80 , -15 , -3.25, 0
น้องๆช่วยกันตอบว่าจำนวนที่กำหนดให้เป็นจำนวนเต็มหรือไม่ ถ้าเป็น เป็นจำนวนเต็มชนิดใด
25 เป็นจำนวนเต็มบวก 9 เป็นจำนวนเต็มบวก -5 เป็นจำนวนเต็มลบ
5.5 ไม่เป็นจำนวนเต็ม 2.0 เป็นจำนวนเต็มบวก 9.80 ไม่เป็นจำนวนเต็ม
-15 เป็นจำนวนเต็มลบ -3.25 ไม่เป็นจำนวนเต็ม 0 เป็นจำนวนเต็มศูนย์
น้องๆ พิจารณาเส้นจำนวนและสังเกตจำนวนที่แตกต่างกันบนเส้นจำนวน 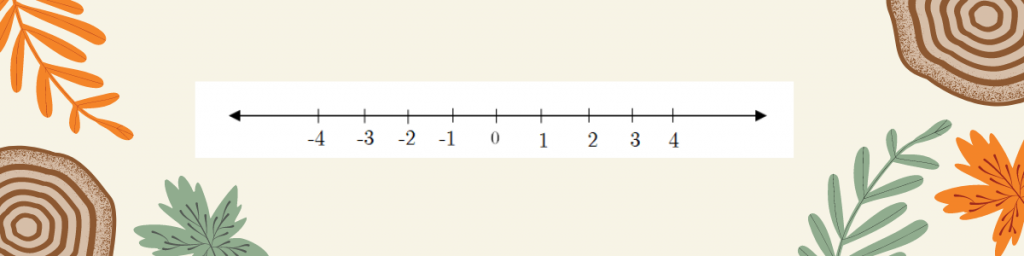
– จำนวนที่อยู่ขวามือของศูนย์แตกต่างกับจำนวนที่อยู่ซ้ายมืออย่างไร (จำนวนที่อยู่ขวามือจะมีค่ามากกว่าจำนวนทางซ้ายมือ)
– ถ้านำจำนวนบนเส้นจำนวนมาเขียนเรียงลำดับจากซ้าย (-4) ไปขวา (4) จำนวนเพิ่มขึ้นหรือลดลงอย่างไร (เพิ่มขึ้น โดยเพิ่มขึ้นทีละ 1)
จากเส้นจำนวน จะเห็นว่า จำนวนเต็มที่อยู่ทางขวาจะมากกว่าจำนวนเต็มที่อยู่ทางซ้ายเสมอ
เช่น 1 อยู่ทางซ้ายของ 2 ดังนั้น 1 น้อยกว่า 2 ใช้สัญลักษณ์ 1 < 2
2 อยู่ทางซ้ายของ 3 ดังนั้น 2 น้อยกว่า 3 ใช้สัญลักษณ์ 2 < 3
4 อยู่ทางขวาของ 3 ดังนั้น 4 มากกว่า 3 ใช้สัญลักษณ์ 4 > 3
3 อยู่ทางขวาของ 2 ดังนั้น 3 มากกว่า 2 ใช้สัญลักษณ์ 3 > 2
1 อยู่ทางขวาของ 0 ดังนั้น 1 มากกว่า 0 ใช้สัญลักษณ์ 1 > 0
-1 อยู่ทางซ้ายของ 0 ดังนั้น -1 น้อยกว่า 0 ใช้สัญลักษณ์ -1 < 0
-2 อยู่ทางซ้ายของ 0 ดังนั้น -2 น้อยกว่า 0 ใช้สัญลักษณ์ -2 < 0
0 อยู่ทางขวาของ -1 ดังนั้น 0 มากกว่า -1 ใช้สัญลักษณ์ 0 > -1
-3 อยู่ทางขวาของ -4 ดังนั้น -3 มากกว่า -4 ใช้สัญลักษณ์ -3 > -4
-5 อยู่ทางซ้ายของ -3 ดังนั้น -5 น้อยกว่า -3 ใช้สัญลักษณ์ -5 < -3
หมายเหตุ จำนวนเต็มยิ่งติดลบเยอะ ยิ่งมีค่าน้อย
การเปรียบเทียบจำนวนเต็มสองจำนวนที่ไม่เท่ากัน เพื่อตัดสินว่าจำนวนใดน้อยกว่าหรือจำนวนใดมากกว่า สามารถพิจารณาโดยใช้เส้นจำนวน คือ จำนวนที่อยู่ทางขวามือมากกว่าจำนวนที่อยู่ทางซ้ายมือเสมอ ดังนั้นจำนวนเต็มลบที่อยู่ทางขวามือจะมีค่ามากกว่าจำนวนเต็มลบที่อยู่ทางซ้ายมือบนเส้นจำนวน หรือจำนวนเต็มลบที่อยู่ทางซ้ายมือบนเส้นจำนวนจะน้อยกว่าจำนวนเต็มลบที่อยู่ทางขวามือบนเส้นจำนวน
ตัวอย่างการเปรียบเทียบจำนวนเต็ม
ตัวอย่างที่ 1 จงเติมเครื่องหมาย > หรือ < ลงในช่องว่างที่กำหนดให้
1) 0 …………. 2 6) -425 …………. -452
2) 0 …………. –2 7) -512 …………. -432
3) –5 ………….. 5 8) -612 …………. 612
4) –5 …………… –7 9) 763 …………. -763
5) -345……… 435 10) -998 …………. -987
วิธีทำ พิจารณาจากเส้นจำนวน
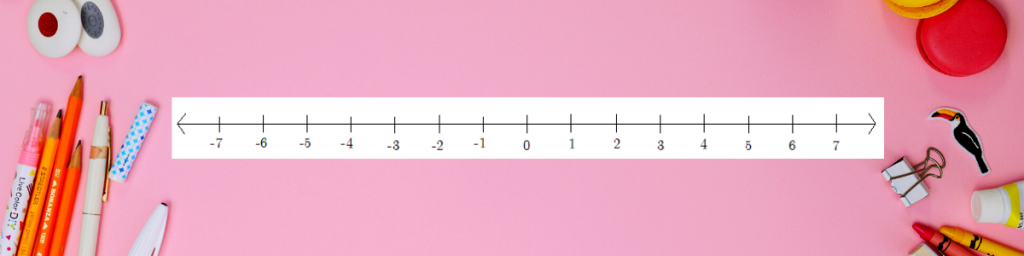
1) 0 อยู่ทางซ้ายของ 2 แสดงว่า 0 < 2
2) 0 อยู่ทางขวาของ -2 แสดงว่า 0 > -2
3) -5 อยู่ทางซ้ายของ 5 แสดงว่า -5 < 5
4) -5 อยู่ทางขวาของ -7 แสดงว่า -5 > -7
ในทำนองเดียวกัน
5) -345 อยู่ทางซ้ายของ 435 แสดงว่า -345 < 435
6) -425 อยู่ทางขวาของ -452 แสดงว่า -425 > -452
7) -512 อยู่ทางซ้ายของ -432 แสดงว่า -512 < -432
8) -612 อยู่ทางซ้ายของ 612 แสดงว่า -612 < 612
9) 763 อยู่ทางขวาของ -763 แสดงว่า 763 > -763
10) -998 อยู่ทางซ้ายของ -987 แสดงว่า -998 < -987
ตัวอย่างที่ 2 จงเรียงลำดับจำนวนต่อไปนี้จากน้อยไปมาก
-
-
-
- -5, -1, 0, -7, 3, -80
- 76, 23, 89, 43, 78, 99
- -23, -76, -56, -28, -78,-34
- -86, -345, 789, -923, -675,345
- -76, 45, 98, -56, -57, 78
-
-
วิธีทำ
-
-
-
- -80, -7, -5, -1, 0, 3
- 23, 43, 76, 78, 89, 99
- -78, -76, -56, -34, -28, -23
- -923, -675, -345, -89, 345,789
- -76, -57, -56, 45, 78, 98
-
-
ตัวอย่างที่ 3 จงเรียงลำดับจำนวนต่อไปนี้จากมากไปน้อย
-
-
-
- 56, 43, 78, 98, 546
- -45, -23, 65, 89, 190
- -865, 345, 54, -654, 564
- -345, 0, 46, 234, -10
- 23, -33, -1, 90, 354, -456
-
-
วิธีทำ
-
-
-
- 546, 98, 78, 56, 43
- 190, 89, 65, -23, -45
- 564, 345, 54, -654, -865
- 234, 46, 0, -10, -345
- 354, 90, 23, -1, -33, -456
-
-
ตัวอย่างที่ 4 ในการวัดอุณหภูมิของจังหวัดทางตอนเหนือของประเทศไทยในฤดูหนาว แสดงด้วยตาราง ดังนี้
| ชื่อจังหวัด |
เลย |
เชียงใหม่ | เชียงราย | แม่ฮ่องสอน | ลำปาง | หนองคาย | ขอนแก่น |
น่าน |
| อุณหภูมิ (องศาเซลเซียส) |
-4 |
-2 | -1 | 0 | 1 | 3 | 6 |
7 |
จงใช้ข้อมูลจากตารางตอบคำถามต่อไปนี้
- จังหวัดใดมีอากาศหนาวมากที่สุด (เลย)
- จังหวัดใดมีอากาศหนาวน้อยที่สุด (น่าน)
- จังหวัดใดมีอากาศหนาวมากที่สุดเป็นอันดับสอง (เชียงใหม่)
- จังหวัดแม่ฮ่องสอนและจังหวัดน่านมีอุณหภูมิแตกต่างกี่องศาเซลเซียส (7 องศาเซลเซียส)
- จังหวัดเลยและจังหวัดลำปางมีอุณหภูมิแตกต่างกี่องศาเซลเซียส (5 องศาเซลเซียส)
หมายเหตุ : อุณหภูมิ ยิ่งติดลบเยอะ อากาศยิ่งหนาว
สรุป
การเปรียบเทียบจำนวนเต็มสองจำนวนที่ไม่เท่ากัน สามารถพิจารณาโดยใช้เส้นจำนวน คือ จำนวนที่อยู่ทางขวามือมากกว่าจำนวนที่อยู่ทางซ้ายมือเสมอ
คลิปวิดีโอ การเปรียบเทียบจำนวนเต็ม
คลิปวิดีโอนี้ได้รวบรวมตัวอย่าง การเปรียบเทียบจำนวนเต็ม เป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค และวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย



















