กราฟของความสัมพันธ์

กราฟของความสัมพันธ์ r คือเซตของจุดในระนาบx, y โดยที่แต่ละจุดคือสมาชิกของความสัมพันธ์ r นั่นเอง อธิบายให้เข้าใจง่ายคือ เมื่อเราได้เซตของความสัมพันธ์ r ที่มีสมาชิกในเซตคือคู่อันดับแล้ว เราก็นำคู่อันดับแต่ละคู่มาเขียนกราฟนั่นเอง

เช่น r = {(1, 1), (1, 2), (2, 2), (3, 4)} นำมาเขียนกราฟของความสัมพันธ์ r ได้ดังนี้

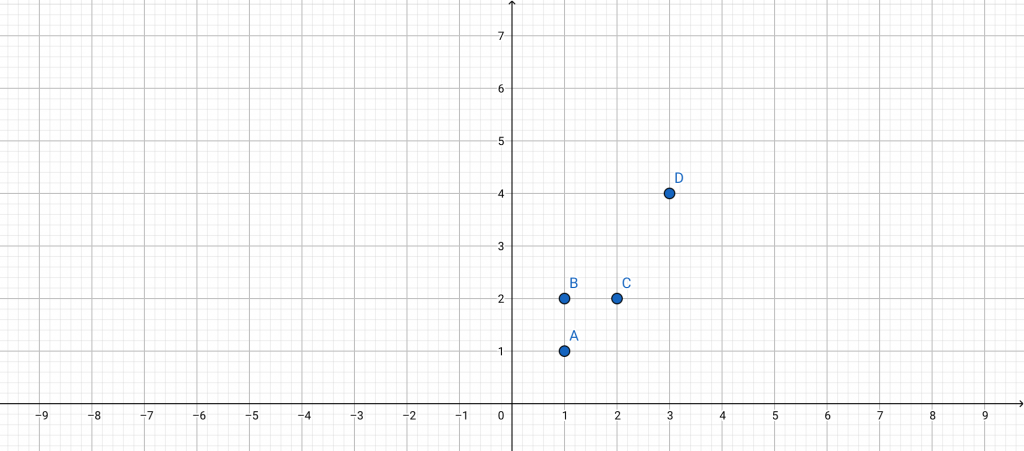
การเขียนกราฟความสัมพันธ์แบบบอกเงื่อนไข

รูปแบบการเขียนแบบบอกเงื่อนไขจะเป็นเหมือนกับการเขียนเซตแบบบอกเงื่อนไข เช่น A = {x : x ∈ R} และ B = {y : y ∈ } เป็นต้น เรามักจะใช้ในกรณีที่ไม่สามารถเขียนแจกแจงสมาชิกทั้งหมดได้ กรณีที่ไม่สามารถแจกแจงสมาชิกได้ทั้งหมด เช่น x เป็นจำนวนจริง จะเห็นได้ว่าจำนวนจริงนั้นมีเยอะมาก บอกไม่หมดแน่ๆ จึงต้องเขียนแบบบอกเงื่อนไขนั่นเอง

เรามาดูตัวอย่างการเขียนกราฟกันค่ะ

ให้ A = {x : x ∈ R} และ B = {y : y ∈ R}

กำหนด r ⊂ A × B และ r = {(x, y) ∈ A × B : y = x²}

ขั้นที่ 1 ให้ลองแทนค่าของจำนวนเต็มบวก x ลงในสมการ y = x²  ที่ต้องแทน x เป็นจำนวนเต็มบวก เพราะเงื่อนไขในเซต A นั่นเอง

แทน x = 0, 1, 2, 3, 4

x = 0 ; y = 0

x = 1 ; y = (1)² = 1

x = 2 ; y = (2)² = 4

x = 3 ; y = (3)² = 9

x = 4 ; y = (4)² = 16

ขั้นที่ 2 เมื่อเราแทนค่า และได้ค่า y มาแล้ว ให้เราเขียนคู่อันดับที่เราได้จากขั้นที่ 1

จะได้คู่อันดับ ดังนี้ (0, 0), (1, 1), (2, 4), (3, 9), (4, 16)

**คู่อันดับที่ได้นี้เป็นเพียงสมาชิกบางส่วนของ r นะคะ เนื่องจากสมาชิกของ r เยอะมาก เราเลยยกตัวอย่างมาบางส่วนเพื่อที่จะเอาไปเขียนกราฟ**

ขั้นที่ 3 นำคู่อันดับที่ได้จากขั้นที่ 2 มาเขียนกราฟ โดยแกนตั้งคือ y แกนนอนคือ x

วิธีการเขียนกราฟคือ นำคู่อันดับแต่ละคู่มามาเขียนบนกราฟ แล้วลากเส้นเชื่อมจุดแต่ละจุด

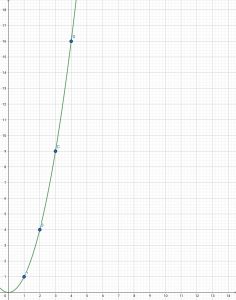
กราฟข้างต้นเป็นการแทนค่า x ด้วยจำนวนจริงบางส่วน

ถ้าเราแทนค่า x ด้วยจำนวนจริงทั้งหมดจะได้กราฟ ดังนี้

กราฟของความสัมพันธ์ในรูปแบบเชิงเส้น

เมื่อให้ x, y เป็นจำนวนจริงใดๆ และ y = ax + b ซึ่งเป็นสมาการเส้นตรง(สมาการเชิงเส้น)

ให้ = {(x, y) : y = x}

จะได้กราฟ r ดังรูป

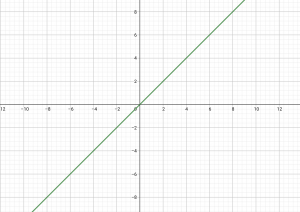
น้องๆสามารถลองแทนจุดบางจุดและลองวาดกราฟดู จะได้กราฟตามรูปข้างบนเลยค่ะ

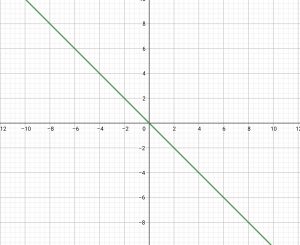
ถ้าให้ = {(x, y) : y = -x}

จะได้กราฟ ดังรูป

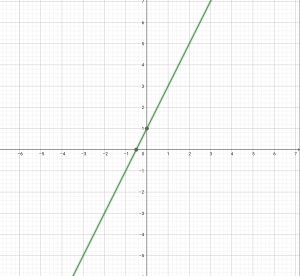
ถ้าให้ = {(x, y) : y = 2x + 1}

จะได้กราฟดังรูป

กราฟของความสัมพันธ์ ในรูปแบบกำลังสอง

ให้ x, y เป็นจำนวนจริงใดๆ สมการ y = ax² + bx +c เป็นสมการกำลังสอง ซึ่งเป็นสมการพาราโบลาที่เราเคยเรียนมาตอนม.ต้นนั่นเอง

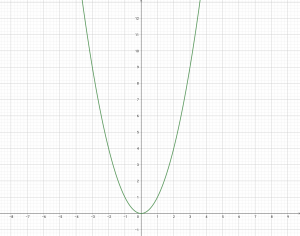
ให้ = {(x, y) : y = 2x²}

เมื่อนำมาเขียนกราฟ จะได้กราฟดังรูป

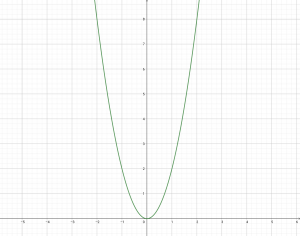
จะเห็นว่ากราฟที่ได้เป็นรูปพาราโบลาหงาย มีจุดวกกลับที่จุด (0, 0)

ถ้าให้ = {(x, y) : x = y²}

เมื่อนำมาเขียนกราฟ จะได้กราฟดังรูป

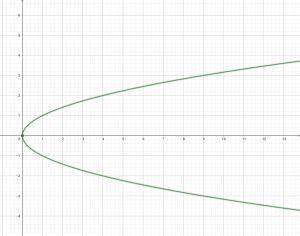
เห็นว่ากราฟที่ได้คือ พาราโบลาตะแคงขวา มีจุดวกกลับที่จุด (0, 0)

ถ้าให้ = {(x, y) : y = -x² + 2x + 5}

เมื่อนำมาเขียนกราฟ จะได้กราฟดังรูป

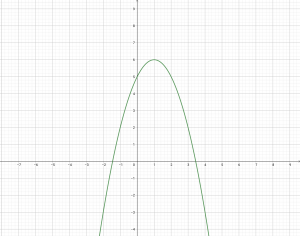
จะได้กราฟพาราโบลาคว่ำ มีจุดวกกลับที่จุด (1, 6)

**น้องๆสามารถแทนค่า x เพื่อหาค่า y แล้วนำคู่อันดับที่ได้มาลองวาดกราฟดูจะได้กราฟตามรูปเลยนะคะ**

กราฟของความสัมพันธ์ ในรูปแบบค่าสัมบูรณ์

ให้ x, y เป็นจำนวนจริงใดๆ และ

กำหนดให้ r = {(x, y) : }

จะได้กราฟ ดังรูป

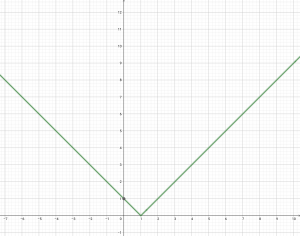
จากกราฟที่น้องๆเห็นทั้งหมดนี้ น้องๆอาจจะไม่ต้องรู้ก็ได้ว่า สมการแบบนี้กราฟต้องเป็นแบบไหน ในบทนี้ อยากให้น้องๆได้ฝึกแทนจุดบนกราฟโดยการแก้สมการหาค่า x, y แล้วนำมาวาดบนกราฟ 

ข้อสำคัญคือ น้องๆจะลากเส้นเชื่อมจุดได้ต้องมั่นใจว่าทุกจุดที่เส้นกราฟผ่านอยู่ในเงื่อนไขที่กำหนดให้ ถ้าเซตที่กำหนดให้เป็นเซตจำกัดอาจจะไม่สามารถลากเส้นแบบนี้ได้ ดังรูปแรกในบทความนี้นั่นเองค่ะ

วิดีโอ กราฟของความสัมพันธ์