เส้นตรง

เส้นตรง มีสมการรูปแบบทั่วไปคือ Ax + By + C = 0 และสมการรูปแบบมาตรฐานของเส้นตรงจะเขียนอยู่ในรูป y = mx + C ซึ่งจะอยู่ในหัวข้อ “สมการเส้นตรง” เส้นตรงหนึ่งเส้นประกอบไปด้วยจุดหลายจุด ซึ่งจุดเหล่านี้จะทำให้เราสามารถหาความชันได้ และเมื่อเราทราบความชันก็จะสามารถหาสมการเส้นตรงได้นั่นเอง

ความชันของเส้นตรง

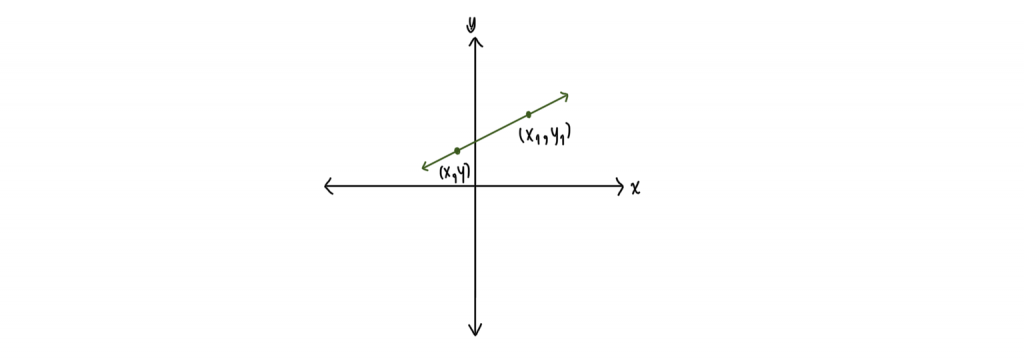
ความชันของเส้นตรง ส่วนใหญ่นิยมใช้ m แทนความชัน การหาความชันนั้นเราจะต้องรู้จุดบนเส้นตรงอย่างน้อย 2 จุด

สมมติให้ และ เป็นจุดบนเส้นตรง L  ดังรูป

จะได้ว่า ความชันของเส้นตรง L หาได้จาก

เส้นตรงที่ขนานกัน

**เส้นตรงที่ขนานกัน ความชันจะเท่ากัน**

ตัวอย่าง

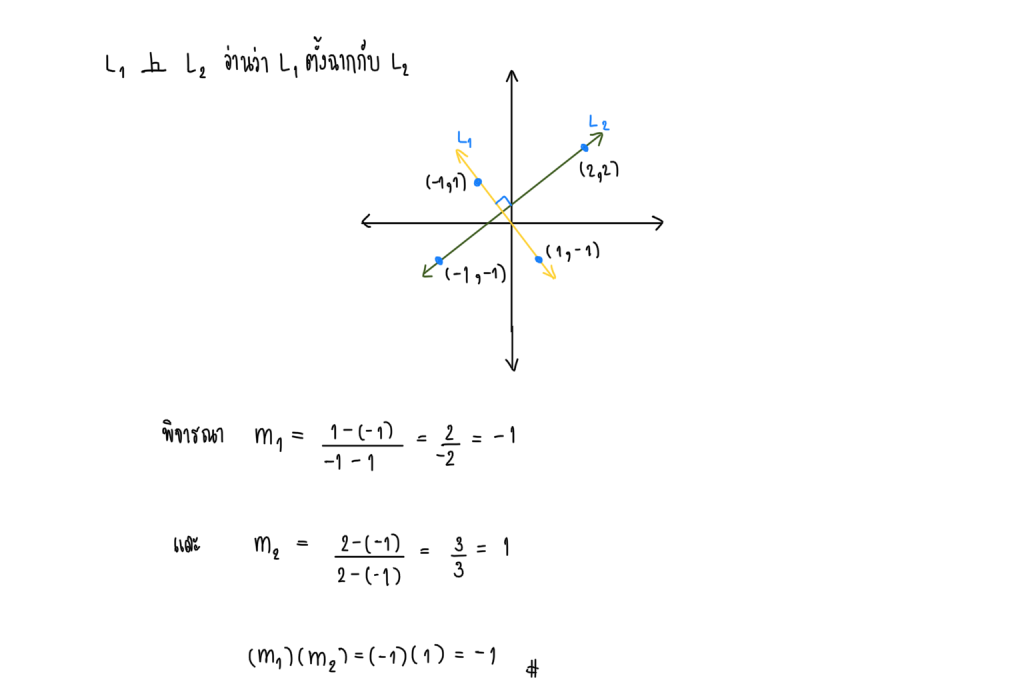
เส้นตรงที่ตั้งฉากกัน

**เส้นตรงสองเส้นตั้งฉากกัน ความชันคูณกันได้เท่ากับ -1**

ตัวอย่าง

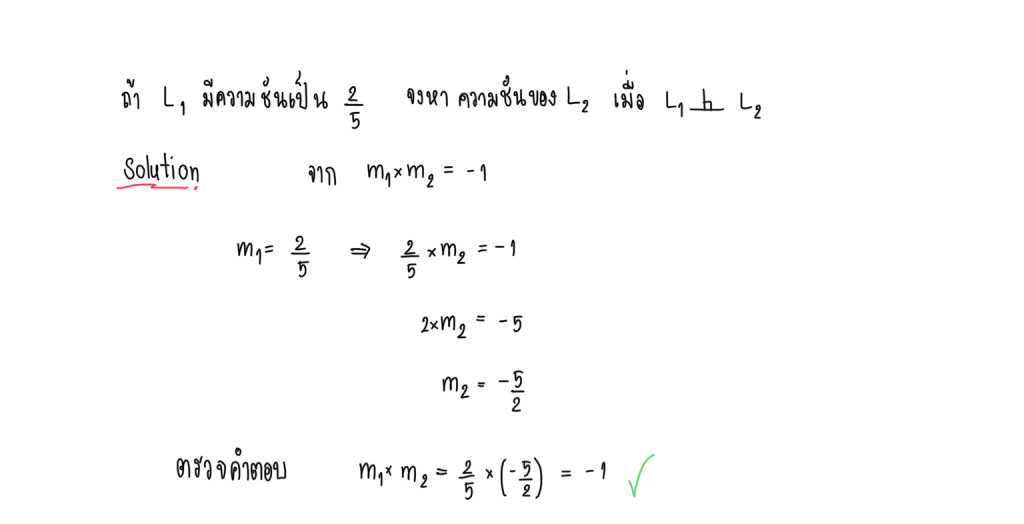
สมการของ เส้นตรง

กรณี 1 เส้นตรงขนานแกน x 

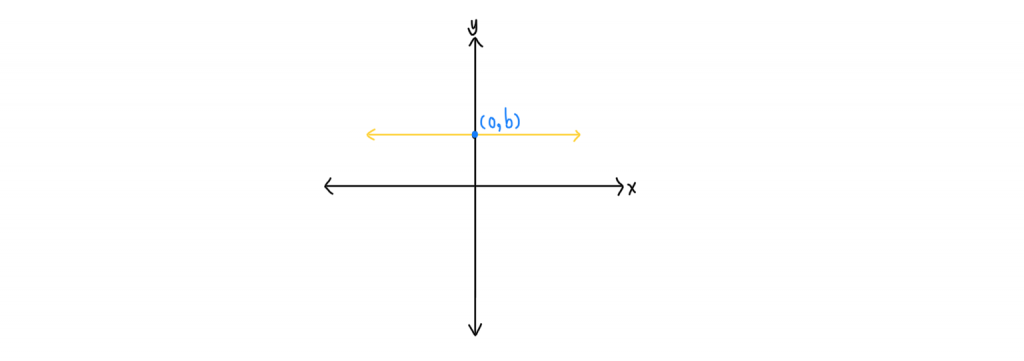
จากรูปจะเห็นว่า เส้นตรงขนานแกน x และตัดแกน y ที่จุด (0, b) ทำให้ได้ว่า ไม่ว่าค่า x จะเป็นเท่าไหร่ ก็จะได้ y = b

ดังนั้น สมการเส้นตรงนี้คือ y = b เมื่อ b คือค่าคงที่

เช่น

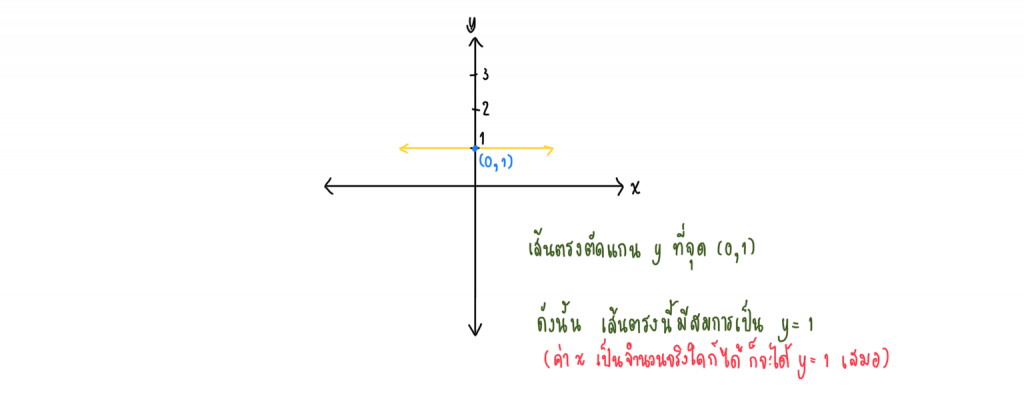
กรณี 2 เส้นตรงทับแกน x

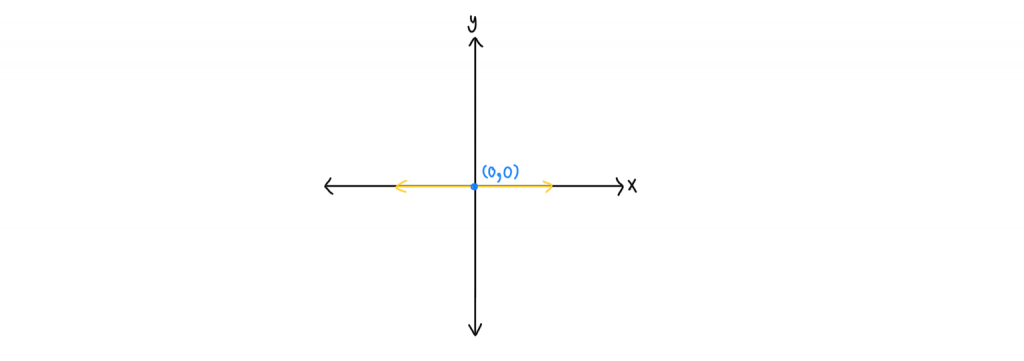
จะเห็นว่า เส้นตรงทับแกน x แกน y ที่จุด (0,0) จะได้ว่า สมการเส้นตรงนี้คือ  y = 0

กรณี 3 เส้นตรงขนานแกน y

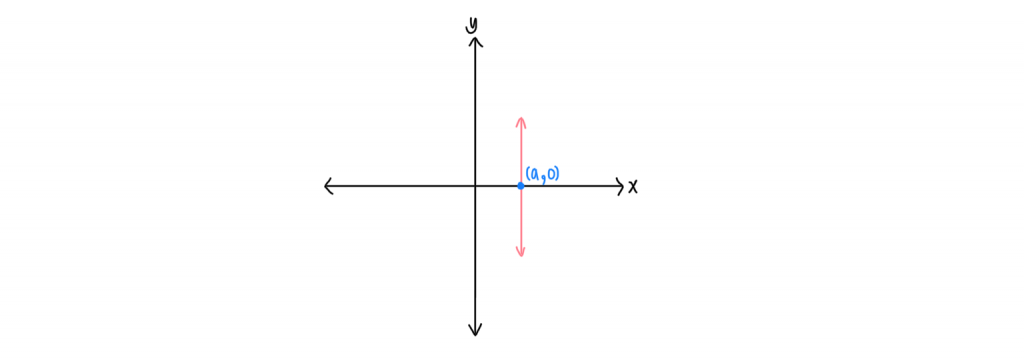
จะเห็นว่าเส้นตรงนั้น ขนานกับแกน y และตัดแกน x ที่จุด (a, 0) ดังนั้น จะได้สมการเส้นตรงเป็น x = a เมื่อ a เป็นค่าคงที่

กรณี 4 เส้นตรงทับแกน y

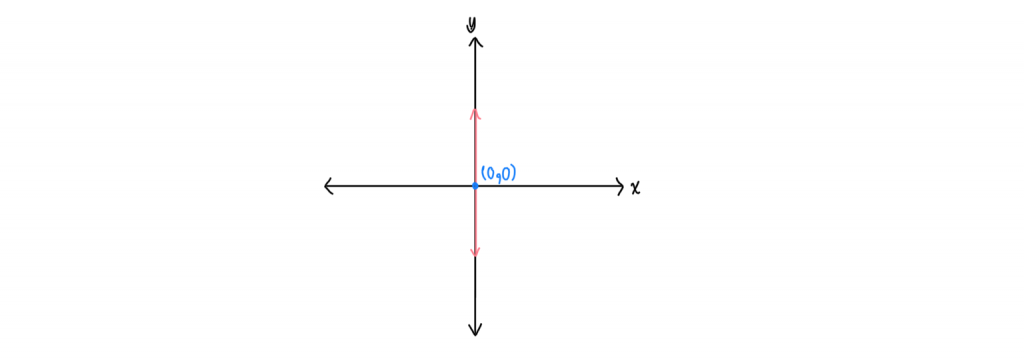
จากรูป เป็นเส้นตรงที่ทับกับแกน y และตัดแกน x ที่จุด (0,0) ดังนั้นจะได้ว่า เส้นตรงนี้คือ เส้นตรง x = 0 

กรณี 5 เส้นตรงไม่ขนานกับแกน x และแกน y

จากกราฟเส้นตรงเราจะได้ว่า ความชันของเส้นตรง คือ และเส้นตรงนี้ผ่านจุด

เมื่อจัดรูปสมการแล้วจะได้ว่า 

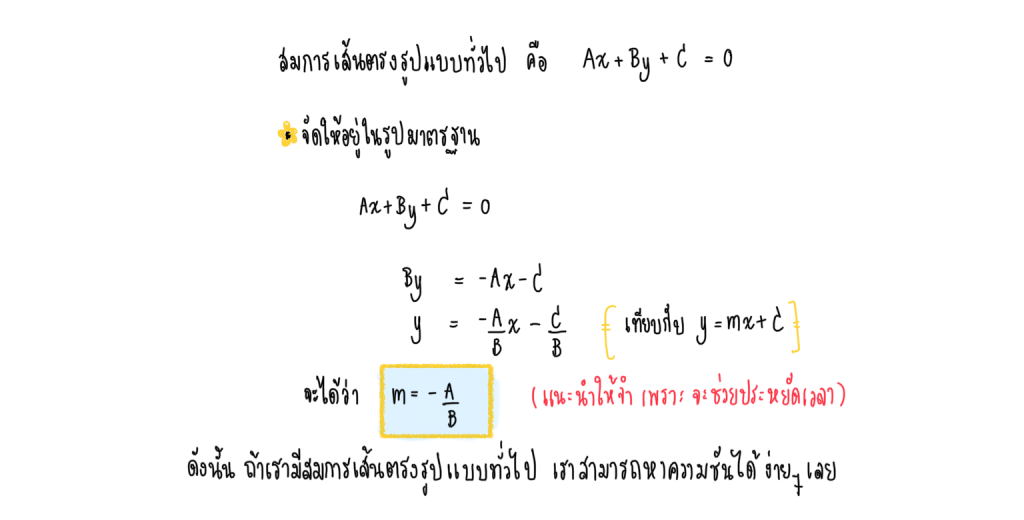
นอกจากรูปแบบมาตรฐานแล้วเราก็ยังมีสมการเส้นตรงรูปแบบทั่วไปด้วย เชื่อว่าน้องๆอาจจะเคยเห็นมาบ้างแล้ว นั่นก็คือ

Ax + By + C = 0

ตัวอย่าง

หาสมการเส้นตรงที่ผ่านจุด (2, 3) และขนานกับเส้นตรง 2x – y +3 = 0

วิธีทำ

วิดิโอทบทวนความรู้

วิดีโอนี้เป็นวิดีโอเกี่ยวกับกราฟของเส้นตรง ซึ่งจะเป็นพื้นฐานให้น้องๆเรียนเรื่องเรขาคณิตวิเคราะห์ ได้เข้าใจมากขึ้น หากน้องๆคนไหนลืมเนื้อหามัธยมต้นไปหมดแล้ว วิดีโอนี้จะช่วยรื้อฟื้นความจำของน้องๆได้ดีเลยค่ะ