นักเรียนรู้จักการหาปริมาตรของปริซึมและทรงกระบอกมาแล้ว ในหัวข้อนี้เราจะต้องนำความรู้ดังกล่าวมาใช้ประกอบในการหาปริมาตรของพีระมิดและกรวย เพื่อให้ได้แนวคิดในการหาปริมาตรของพีระมิดและกรวยให้นักเรียนทำกิจกรรมต่อไปนี้
ปริมาตรพีระมิดและทรงกรวย
ในหัวข้อนี้เราจะต้องนำความรู้ดังกล่าวมาใช้ประกอบในการหาปริมาตรของพีระมิดและกรวย เพื่อให้ได้แนวคิดในการหาปริมาตรของพีระมิดและกรวยให้นักเรียนทำกิจกรรมต่อไปนี้
ปริมาตรพีระมิด
1. ใช้กระดาษแข็งสร้างพีระมิดฐานเปิด ตามที่กำหนดให้ต่อไปนี้
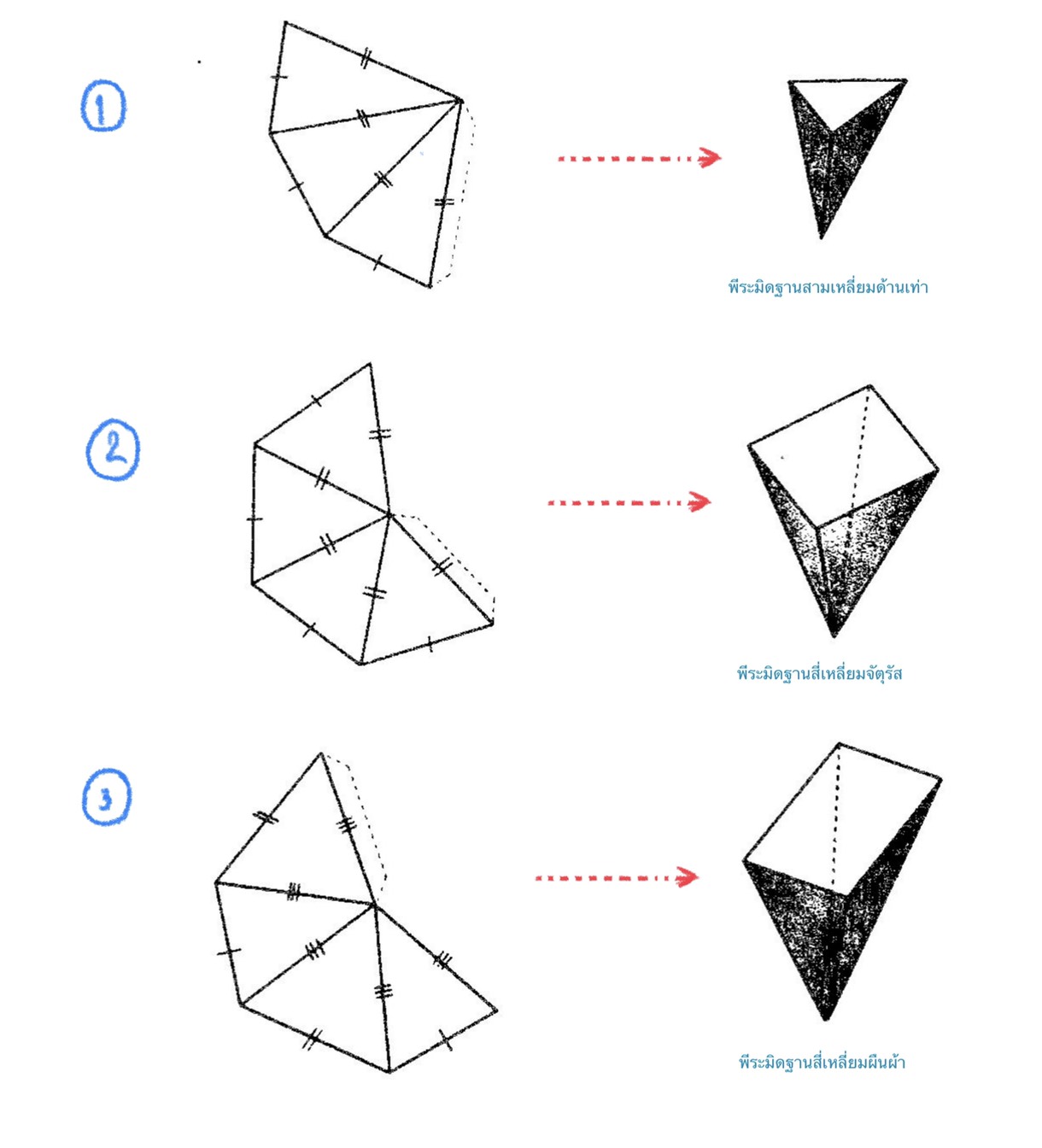
2. สำหรับพีระมิดแต่ละรูปในข้อ 1 ให้สร้างปริซึมฐานเปิดหนึ่งข้างที่มีความสูงเท่ากับความสูงของพีระมิด และมีพื้นที่ฐานเท่ากับพื้นที่ฐานของพีระมิด
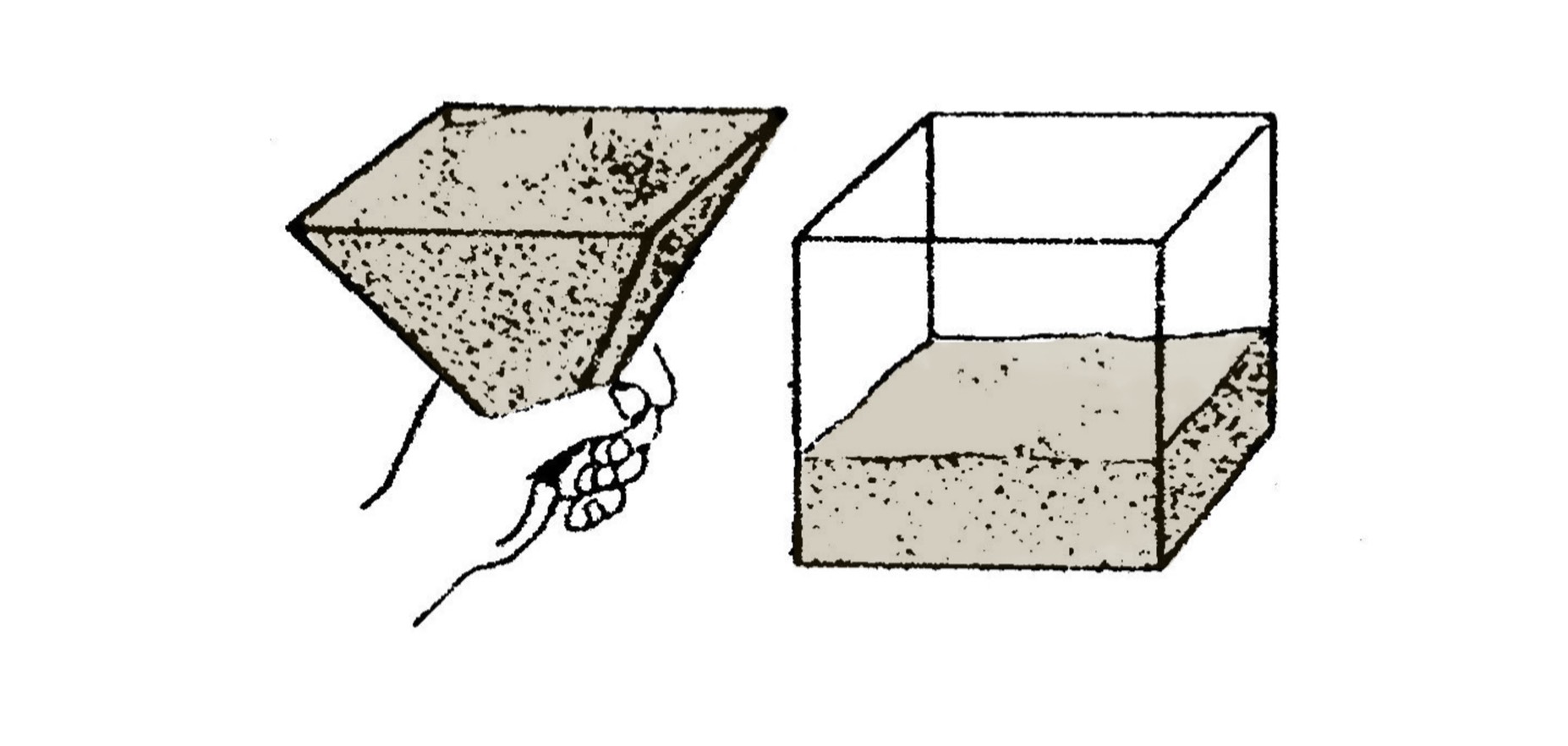
3. ใช้พีระมิดฐานสี่เหลี่ยมผืนผ้าที่สร้างไว้มาตวงทราย โดยใส่ทรายให้เต็มพีระมิดฐานสี่เหลี่ยมผืนผ้า แล้วเททรายจากพีระมิดใส่ลงในปริซึมที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากัน
4. หาว่าจะต้องเททรายจากพีระมิดที่มีทรายเต็มกี่ครั้ง จึงจะได้ทรายเต็มปริซึมพอดี
5. ทำตามข้อ 3 และข้อ 4 ซ้ำอีกโดยเปลี่ยนเป็นพีระมิดฐานสามเหลี่ยมด้านเท่ากับปริซึมที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากัน หรือใช้พีระมิดฐานสี่เหลี่ยมจัตุรัสกับปริซึมที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากัน
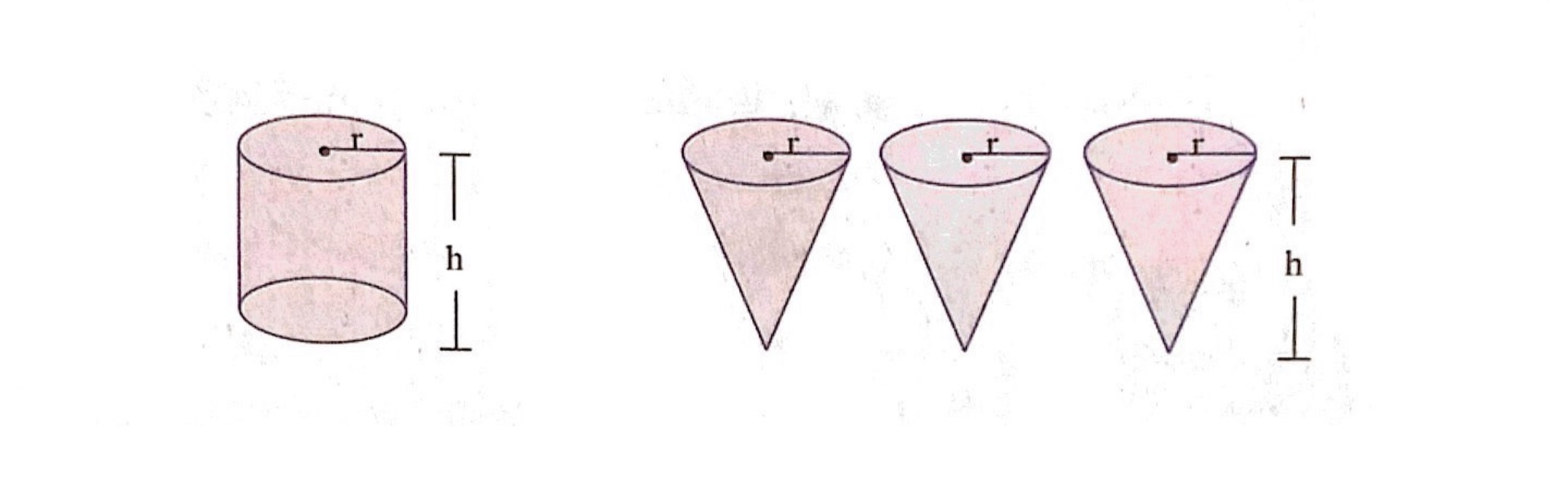
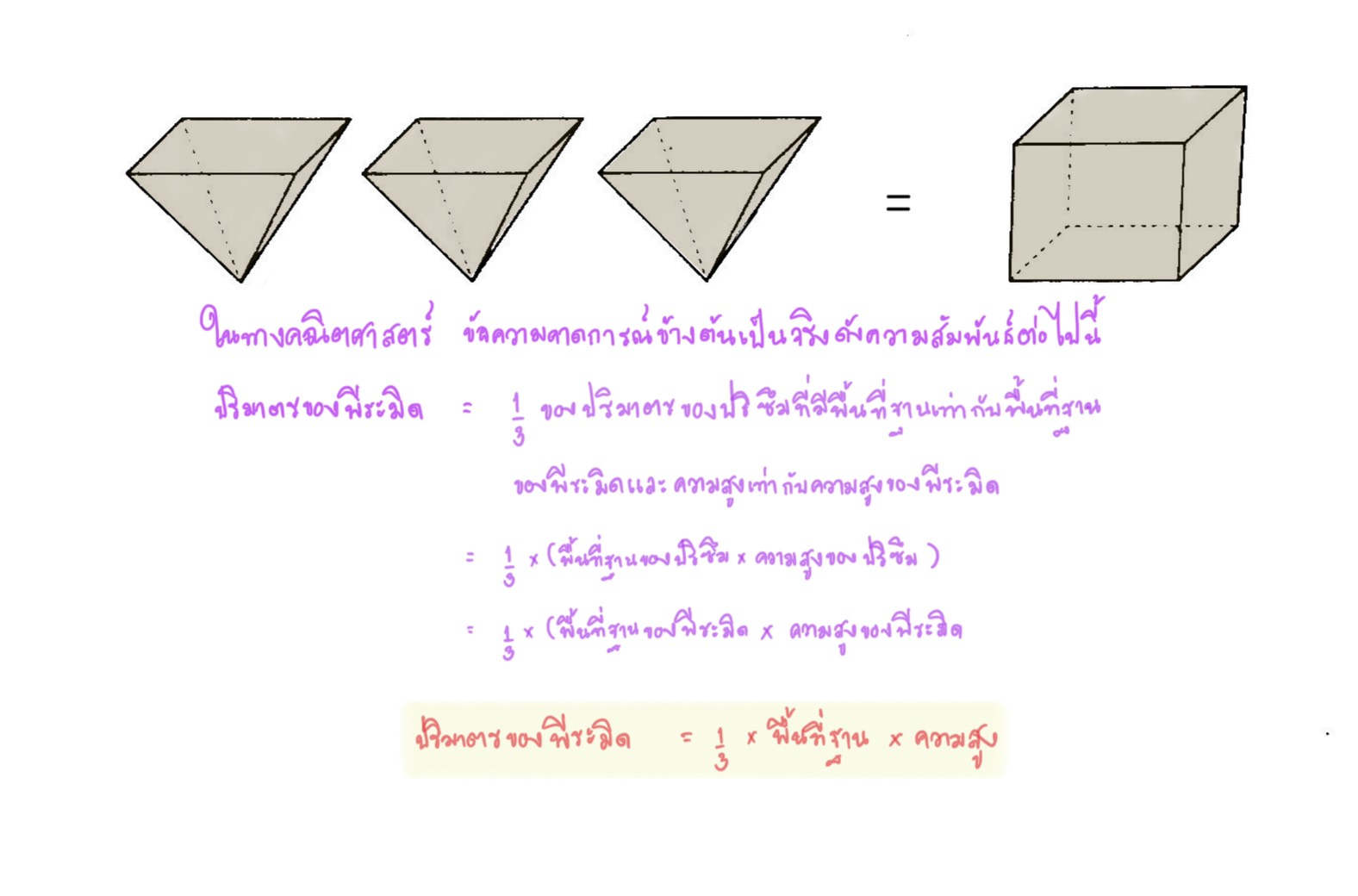
จากการทำกิจกรรมข้างต้น เราจะพบว่า ต้องเททรายจากพีระมิดใส่ลงในปริซึมที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากันจำนวนสามครั้ง จึงจะได้ทรายเต็มปริซึมพอดี เราจึงคาดการณ์ว่าปริมาตรของพีระมิดเป็นหนึ่งในสามของปริมาตรของปริซึมที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากัน ซึ่งอาจแสดงความสัมพันธ์ด้วยรูปภาพได้ดังนี้
ปริมาตรทรงกรวย
เราทราบมาแล้วว่า รูปหลายเหลี่ยมด้านเท่ามุมเท่าที่มีจำนวนด้านมาก ๆ จะมีปริมาตรของกรวยรูปร่างใกล้เคียงกับวงกลม ดังนั้นกรวยจึงมีลักษณะใกล้เคียงกับพีระมิดที่ฐานเป็นรูปหลายเหลี่ยมด้านเท่ามุมเท่าที่มีจำนวนด้านมาก ๆ
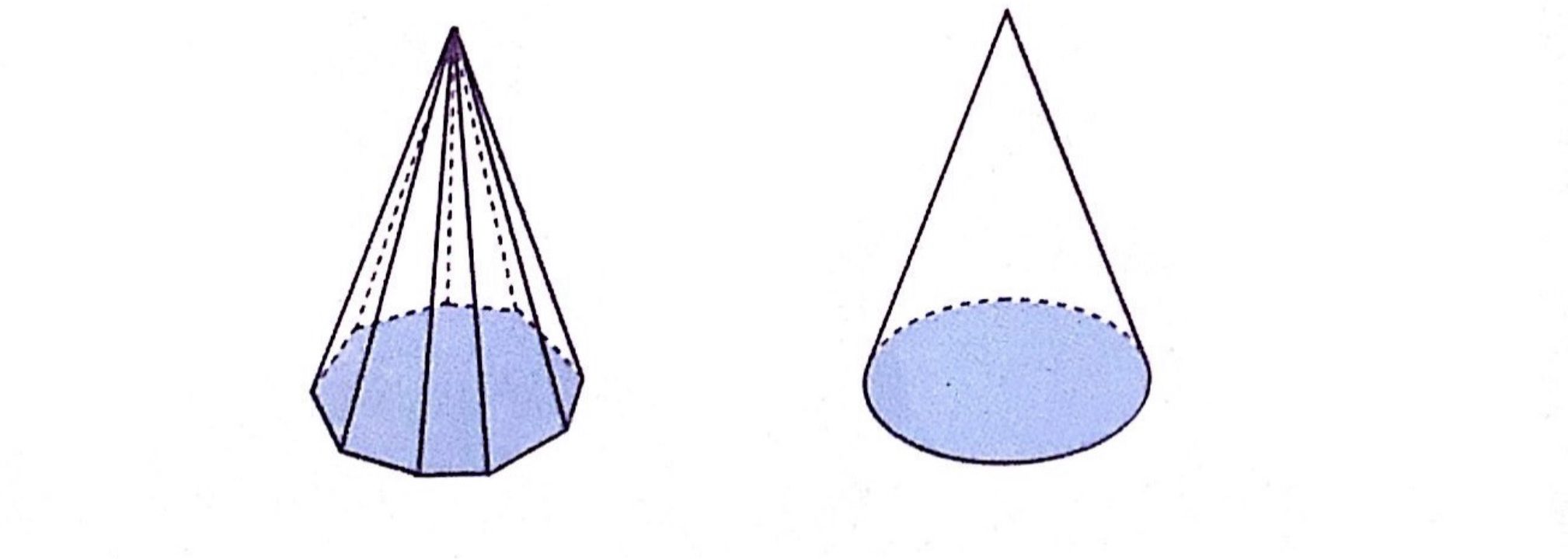
เราได้เห็นความสัมพันธ์ของปริมาตรของพีระมิดกับปริซึมที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากันมาแล้ว ปริมาตรของกรวยที่สัมพันธ์กับปริมาตรของทรงกระบอกในทำนองเดียวกัน กล่าวคือ

เพื่อเป็นการตรวจสอบการหาปริมาตรของกรวยข้างต้น เราอาจทำการทดลองเททรายจากทรงกระบอกที่มีพื้นที่ฐานเท่ากันและความสูงเท่ากันกับของกรวย เราจะพบว่า เททรายลงในกรวยที่มีขนาดเท่ากันได้เต็ม 3 อันพอดี ซึ่งอาจแสดงความสัมพันธ์ด้วยรูปภาพได้ดังนี้