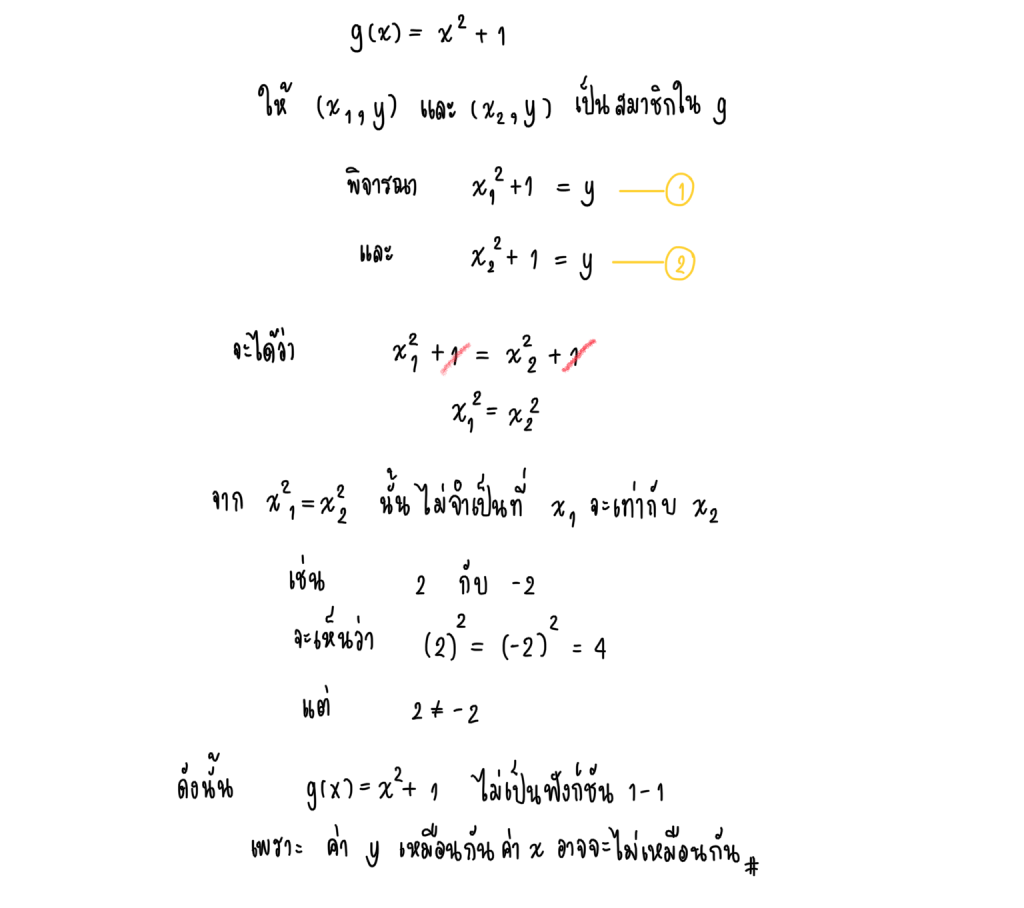ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง

ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง เป็นการส่งสมาชิกจากของเซตหนึ่งเรียกเซตนั้นว่าโดเมน ส่งไปให้สมาชิกอีกเซตหนึ่งเซตนั้นเรียกว่าเรนจ์ จากบทความก่อนหน้าเราได้พูดถึงฟังก์ชันและการส่งสมาชิกในเซตไปแล้วบางส่วน ในบทความนี้เราจะได้ทำความเข้าใจเกี่ยวกับฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งมากขึ้น

จากที่เรารู้ว่าเซตของคู่อันดับเซตหนึ่งจะเป็นฟังก์ชันได้นั้น สมาชิกตัวหน้าต้องไปเหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งเป็นการกำหนดขอบเขตให้ฟังก์ชันนั้นแคปลงกว่าเดิม

เช่น {(1, a), (2, b), (3, a), (4, c)}  จากเซตของคู่อันดับเราสมารถตอบได้เลยว่าเป็นฟังก์ชัน เพราะสมาชิกตัวหน้าไม่เหมือนกัน

แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง คือการที่เรามีเซต 2 เซต แล้วเราส่งสมาชิกในเซตหนึ่งไปอีกเซตหนึ่ง ขอบเขตมันเลยแคบลง

เช่น A ={1, 2, 3, 5}  B = {s, t, u}

ฟังก์ชันจาก A ไป B คือ {(1, s), (2, u), (2, t), (5, s)} จะเห็นว่าฟังกก์ชันถูกสร้างขอบเขตให้เลือกแค่สมาชิกจากในเซต 2 เซตนี้เท่านั้น ไม่สามารถหยิบสมาชิกจากเซตอื่นๆมาได้

ฟังก์ชันจาก A ไป B

f เป็นฟังก์ชันจาก A ไป B คือการส่งสมาชิกจากเซต A ไปยังเซต B โดย สมาชิกในเซต A จะถูกส่งตัวละครั้ง ไปยังเซต B ซึ่งไม่จำเป็นที่เซต B จะถูกใช้จนหมด นั่นก็คือเรนจ์ของฟังก์ชันเป็นสับเซตของ B เขียนแทนด้วย f : A → B

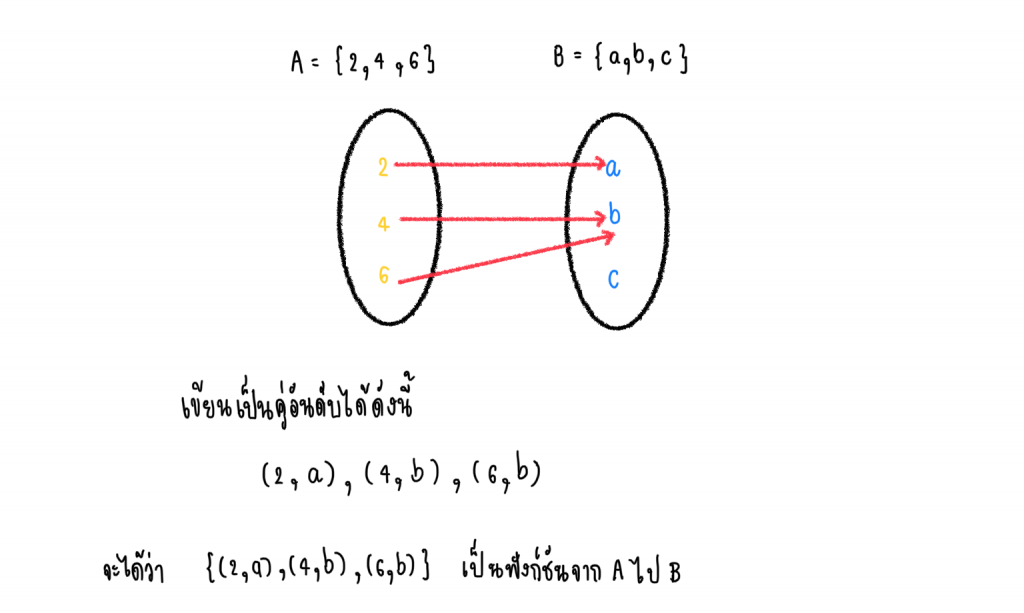
เช่น ให้ A = {2, 4, 6} และ B ={a, b, c}

ฟังก์ชันจาก A ไป B สามารถเขียนได้ดังนี้

ฟังก์ชันจาก B ไป A

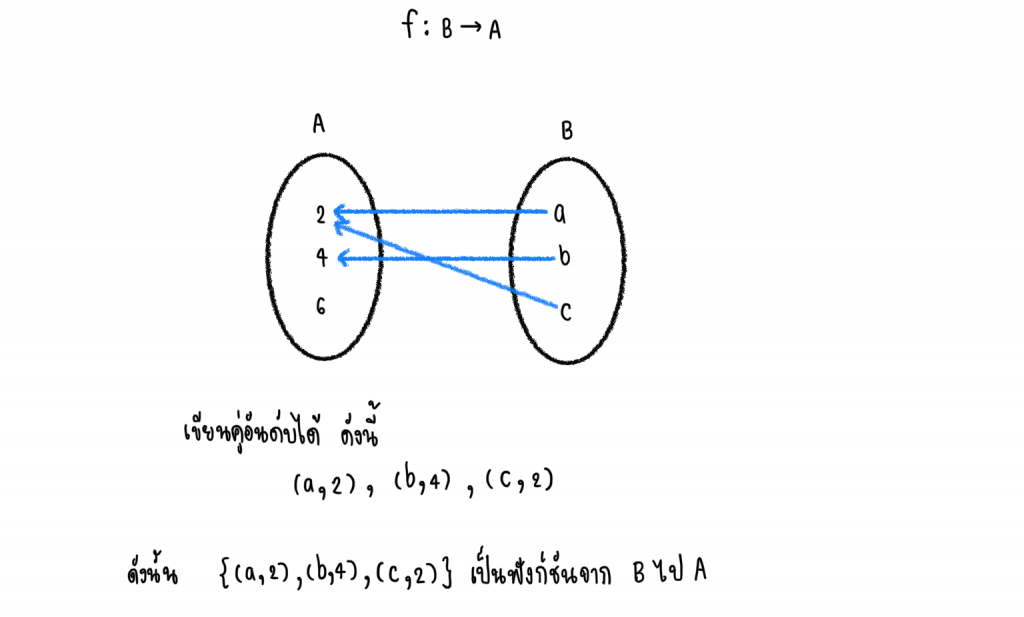
** ฟังก์ชันคู่อันดับข้างต้นเป็นเพียงตัวอย่างเพื่อให้รู้ว่าการส่งฟังก์ชันจากเซตไปอีกเซตเป็นแบบไหน คู่อันดับอาจจะเป็นคู่อื่นนอกเหนือจากที่ยกตัวอย่างมา แต่! ต้องอย่าลืมว่า “ตัวหน้าต้องต่างกัน และต้องมาจากเซตที่กำหนดให้เท่านั้น” นะคะ**

ฟังก์ชันจาก A ไปทั่วถึง B

ฟังก์ชันจาก A ไปทั่วถึง B เป็นการส่งสมาชิกจากเซต A ไปยังสมาชิกใน B ครบทุกตัว ดังนั้นจะได้ว่า เรนจ์ของฟังก์ชันคือ เซต B เขียนแทนด้วย

Keyword คือ ทั่วถึง : แปลง่ายๆว่า A ไปยัง B อย่างทั่วถึง แสดงว่าสมาชิกใน B ต้องโดนจับคู่ทุกตัว

ตัวอย่างเช่น

ให้ A = {2, 4, 6, 7} และ B ={a, b, c}

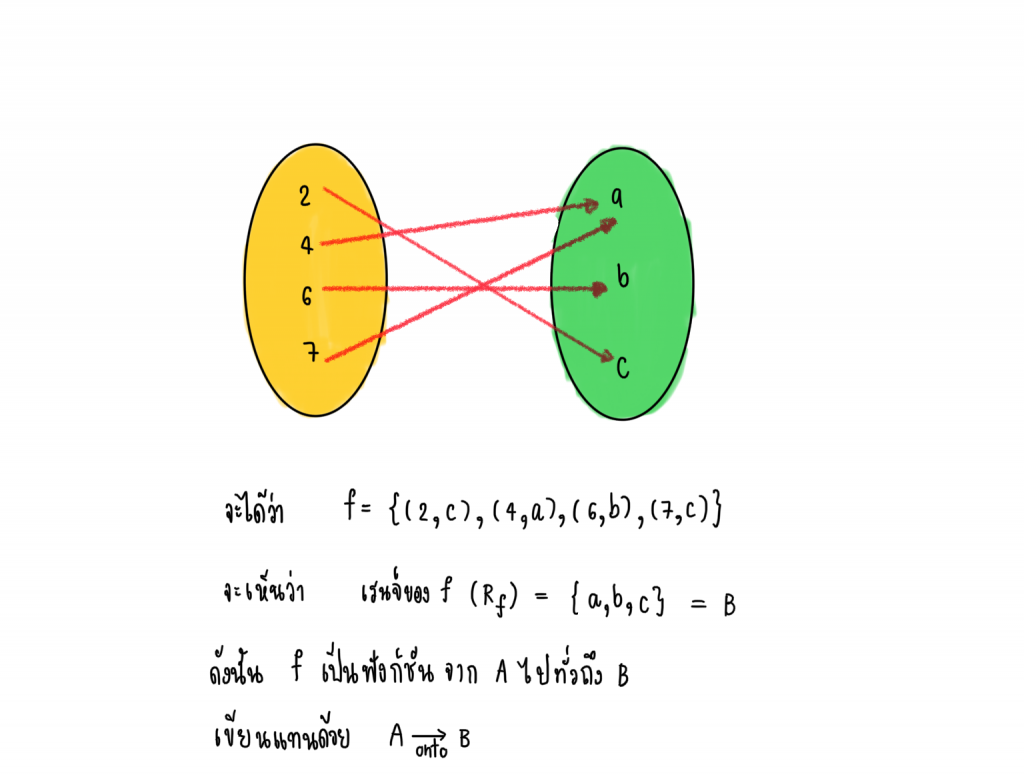
ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B

ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B เป็นการส่งสมาชิกจากเซต A ไปยังสมาชิก B โดยที่สมาชิกใน B 1 ตัว จะคู่กับ สมาชิกใน A เพียงหนึ่งตัวเท่านั้น

เขียนแทนด้วย 

Keyword ก็คือ 1 ต่อ 1 : เหมือนกับเราจับคู่กับเพื่อน ตัวเรา 1 คน ก็ต้องคู่กับเพื่อนอีก 1 คนเท่านั้นจะไปคู่กับคนอื่นอีกไม่ได้

ดังนั้นสำหรับฟังก์ชันหนึ่งต่อหนึ่ง ถ้ามีคู่อันดับสองคู่ที่สมาชิกตัวหลังเท่ากันแล้วจะได้ว่าสมาชิกตัวหน้าจะต้องเท่ากัน

ตัวอย่างเช่น

ให้ A = {2, 4, 6} และ B ={a, b, c}

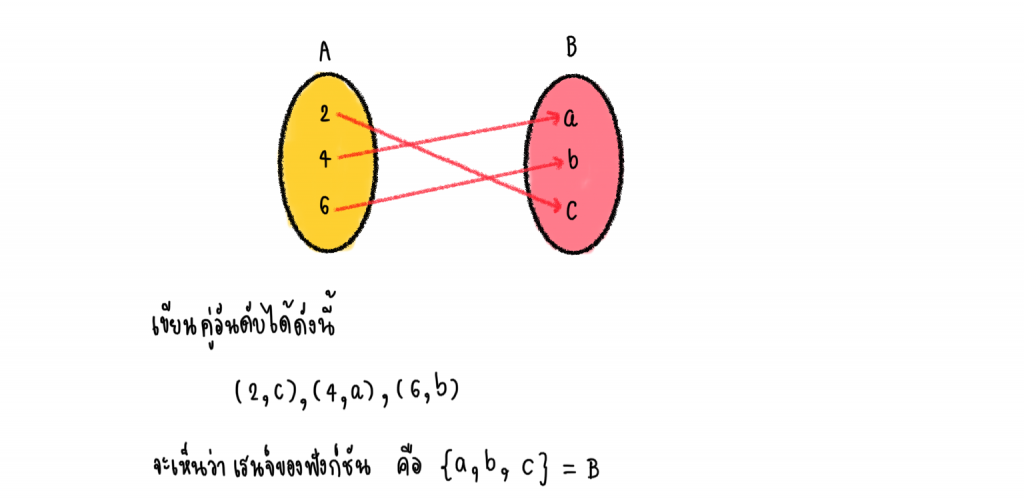
ดังนั้น {(2, c), (4, a), (6, b)} เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B

จากตัวอย่างข้างต้นนอกจากจะเป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B แล้ว ยังเป็นฟังก์ชันจาก A ไปทั่วถึง B อีกด้วย

ดังนั้นจะได้ว่า {(2, c), (4, a), (6, b)} เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไปทั่วถึง B เขียนแทนด้วย

ตัวอย่าง ฟังก์ชันจากเซตไปอีกเซตหนึ่ง

1.) จงตรวจสอบว่า f = {} เป็นฟังก์ชันหนึ่งต่อหนึ่งหรือไม่

เนื่องจากฟังก์ชันหนึ่งต่อหนึ่ง ถ้ามีคู่อันดับ 2 คู่ ที่ สมาชิกตัวหลังเท่ากัน จะได้ว่าสมาชิกตัวหน้าก็เท่ากันด้วย

ดังนั้น ถ้าให้คู่อันดับ 2 คู่มี y เป็นสมาชิกตัวหลังและให้ เป็นสมาชิกตัวหน้าของคู่อันดับดังกล่าว ถ้า f เป็นฟังก์ชันหนึ่งต่อหนึ่งเราจะต้องแสดงให้ได้ว่า

2.) f(x) = 2x + 1 เป็นฟังก์ชันจาก R ไปทั่วถึง R หรือไม่ เพราะเหตุใด

ฟังก์ชันจาก R ไปทั่วถึง R หมายความว่า โดเมนของฟังก์ชันคือ R และเรนจ์ของฟังก์ชันก็คือ R เหมือนกัน

ตอบ f เป็นฟังก์ชันจาก R ไปทั่วถึง R เพราะ จาก โดเมน คือ  R ซึ่งเป็นจำนวนจริง จากสมบัติของจำนวนจริง (สมบัติปิดการบวกและการคูณ) ทำให้ได้ว่าไม่ว่าจะแทน x เป็นจำนวนจริงตัวใด เมื่อบวกหรือคูณกันแล้วก็ยังได้จำนวนจริงเหมือนเดิม จึงได้ว่าเรนจ์ของ f คือ R

3.) กำหนดให้ A = {1, 2, 3}, B = {2, 3, 4}

3.1) = {(1, 3), (2, 4), (3, 3)} เป็นฟังก์ชันใดบ้างบ้าง

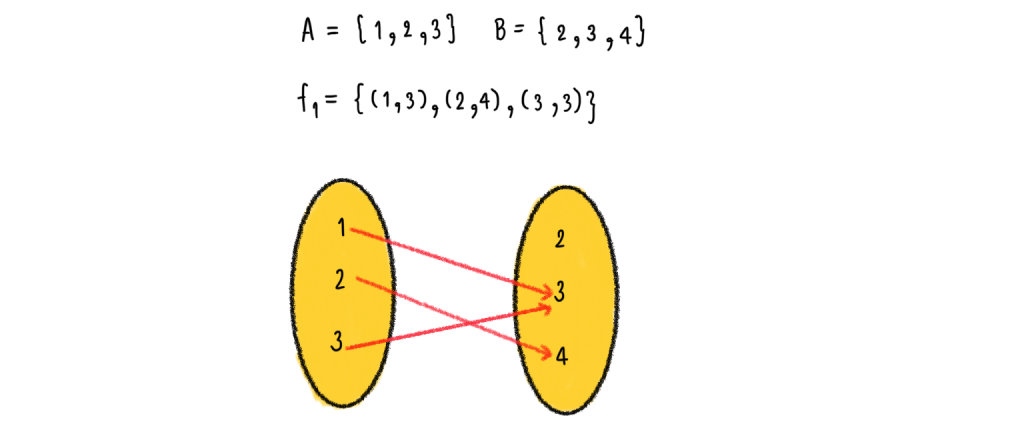
จากรูป จะเห็นว่า เรนจ์ของ f เป็นสับเซตของ B

ดังนั้นจะได้ว่า เป็นฟังก์ชันจาก A ไป B

3.2) = {(2, 2), (3, 3) , (4, 1)} เป็นฟังก์ชันใดบ้าง

จาก คู่อันดับข้างต้น สังเกตดู (4, 1) ตัวหน้าคือสมาชิกของเซต B และตัวหลังเป็นสมาชิกของเซต A แสดงว่า ฟังก์ชันนี้เป็นฟังก์ชันจาก B ไป A แน่นอน

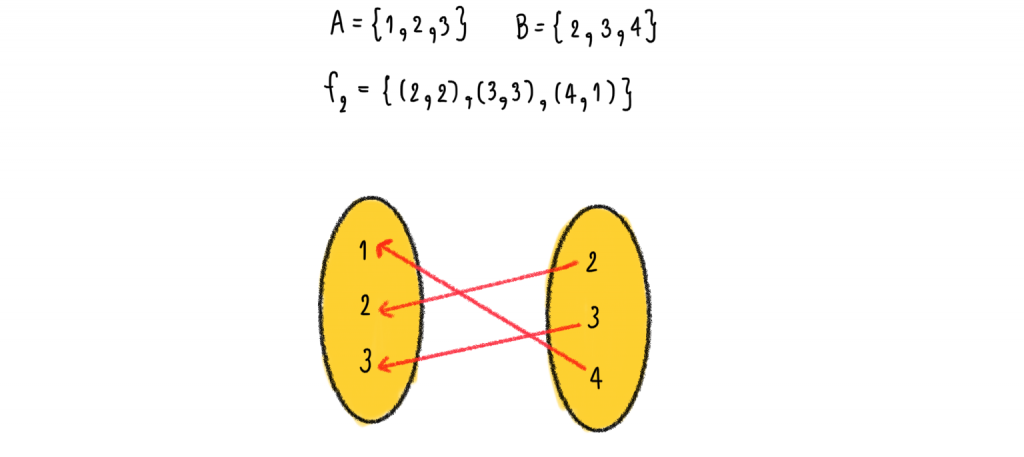
จากรูป จะเห็นว่า สมาชิกในเซต A โดนจับคู่แค่ตัวละครั้ง ทั้ง A และ B สมาชิกทุกตัวมีคู่หมด

ดังนั้น เป็นฟังก์ชัน 1-1 จาก B ไปทั่วถึง A

4.) g(x) = x² + 1 เป็นฟังก์ชัน 1-1 หรือไม่