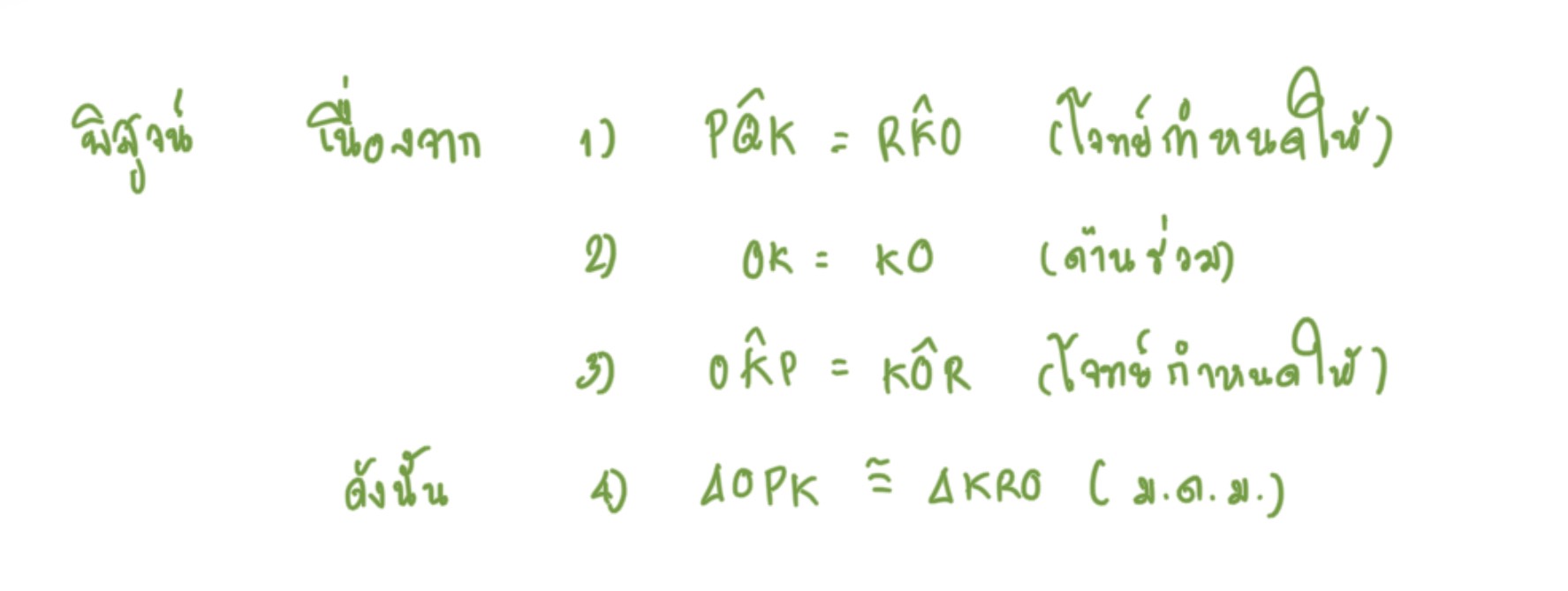สามเหลี่ยมที่เท่ากันทุกประการแบบ มุม-ด้าน-มุม

ในบทความนี้จะกล่าวถึงหลักการของการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยมแบบ มุม-ด้าน-มุม

tucksaga

คณิตศาสตร์, คณิตศาสตร์ ม.2, ม.2

Add LINE friends for one click to find article.

เมื่อเราต้องการจะพิสูจน์ถึงสิ่งของใดๆว่ามีความเท่ากันทุกประการ เราจำเป็นต้องมีหลักการที่นำมาใช้ได้จริง ดังเช่นในบทความนี้ที่กล่าวถึงรูปสามเหลี่ยมที่เท่ากันทุกประการโดยใช้ความยาวของด้าน 1ด้าน และ มุม 2 มุม ในการพิสูจน์

สามเหลี่ยมที่เท่ากันทุกประการแบบ มุม-ด้าน-มุม

ในทางคณิตศาสตร์เมื่อสามารถเคลื่อนที่รูปเรขาคณิตรูปหนึ่งไปทับรูปเรขาคณิตอีกรูปหนึ่งได้สนิท จะกล่าวว่ารูปเรขาคณิตสองรูปนั้น เท่ากันทุกประการ

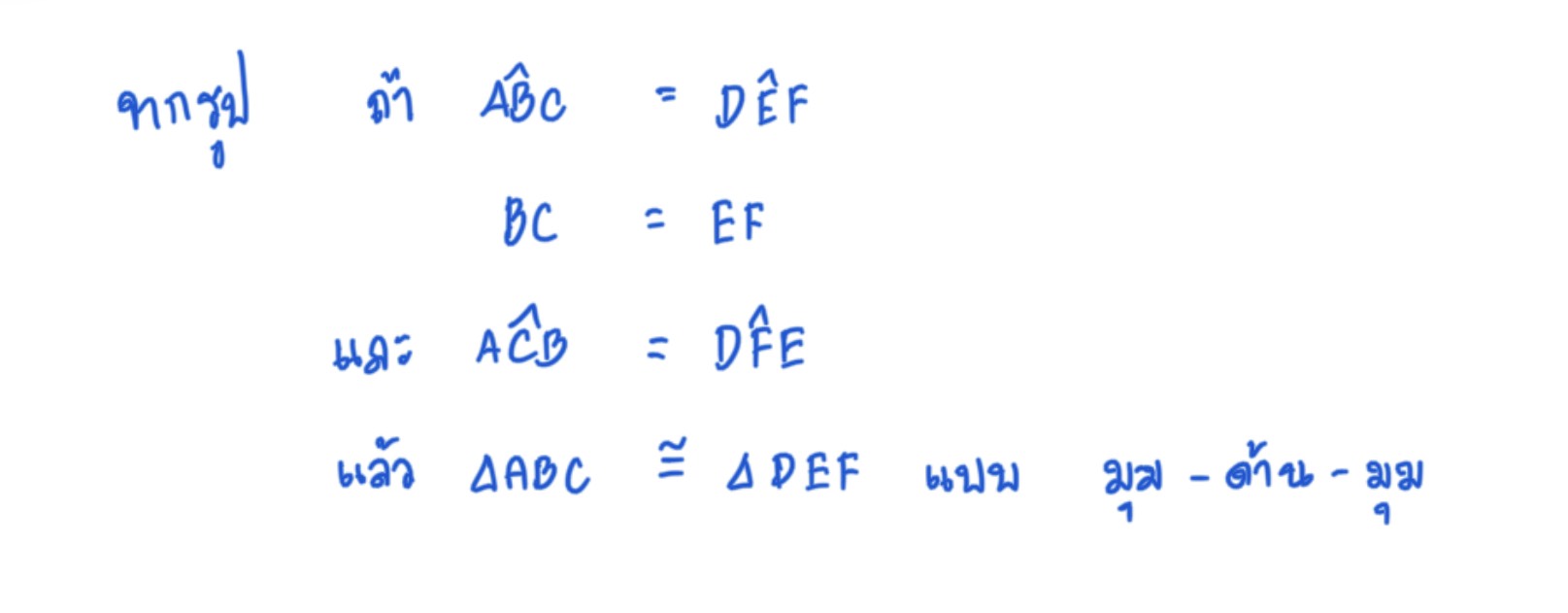
ถ้ารูปสามเหลี่ยมสองรูปใดๆ มีมุมที่มีขนาดเท่ากันสองคู่ และด้านซึ่งเป็นแขนร่วมของมุมทั้งสองมีขนาดยาวเท่ากันด้วยแล้ว รูปสามเหลี่ยมสองรูปนั้นจะเท่ากันทุกประการ

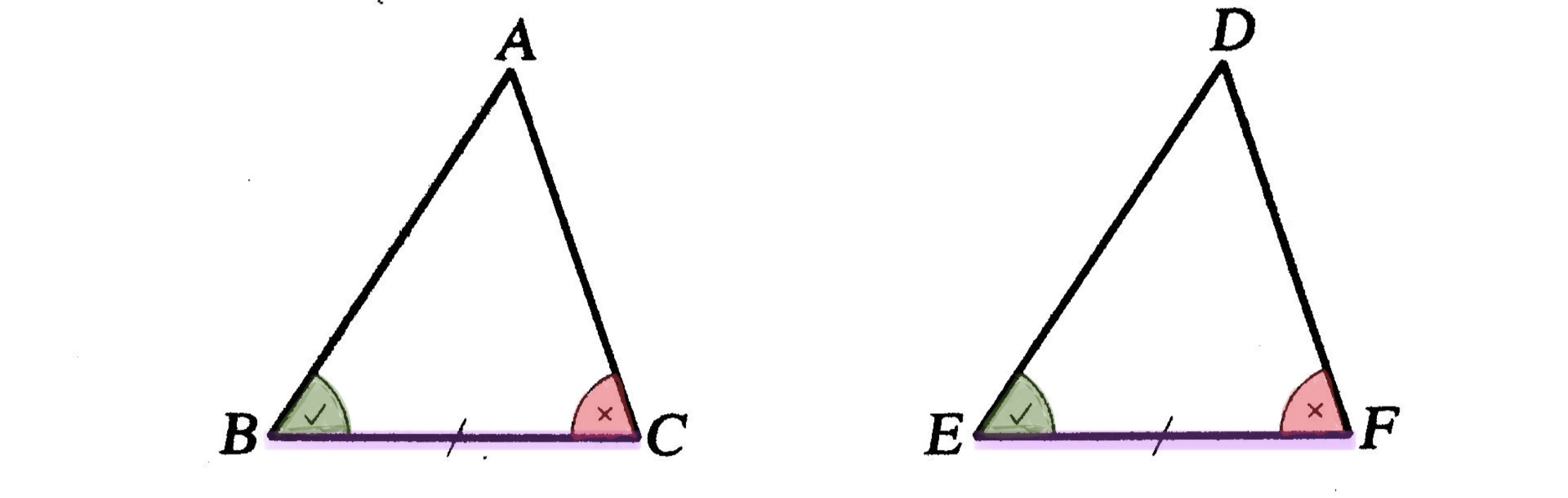
ตัวอย่างที่ 1

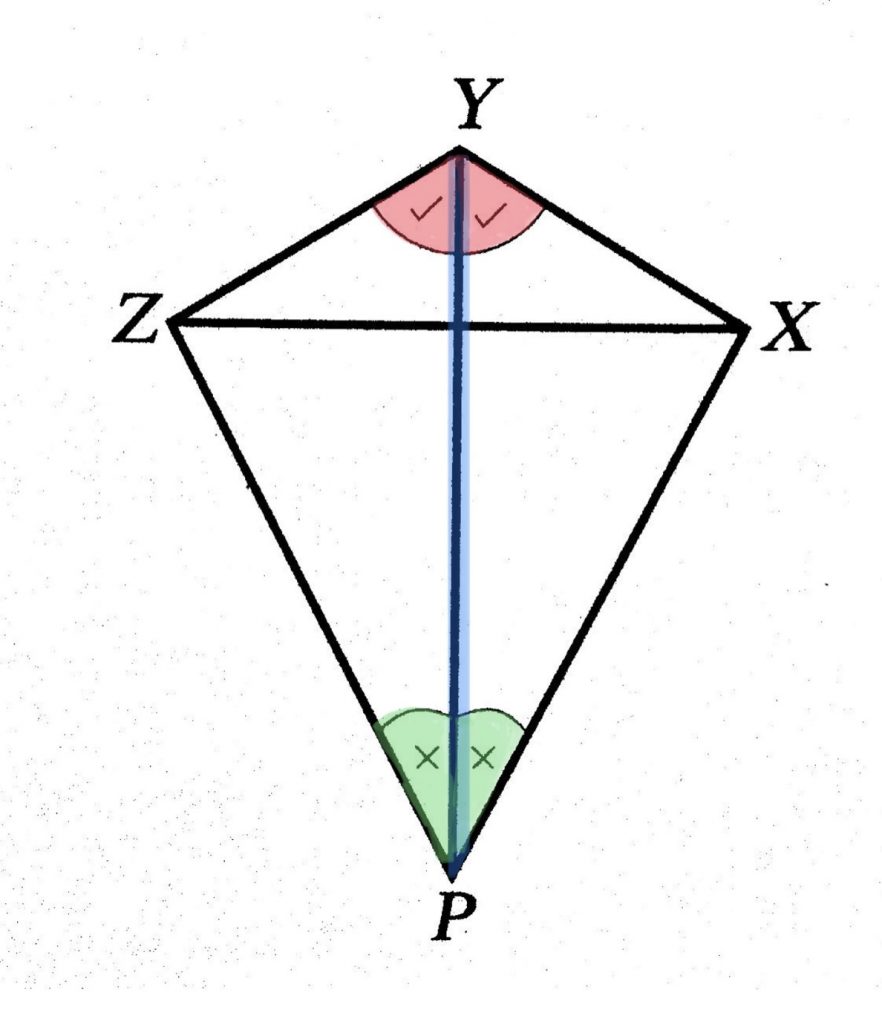
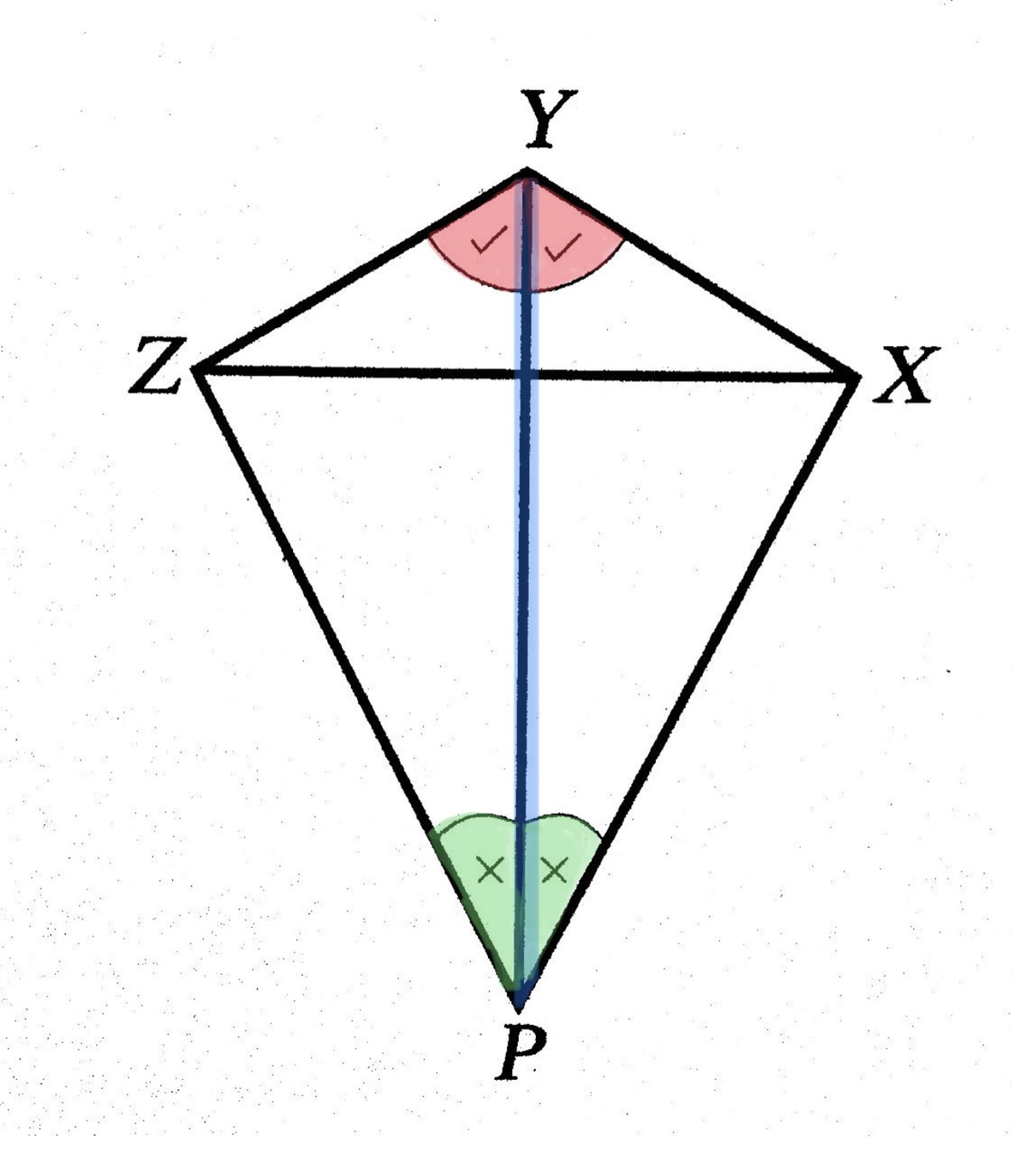
จงพิสูจน์ว่า PX = PZ เมื่อ รูปสี่เหลี่ยม PXYZ เป็นสี่เหลี่ยมรูปว่าว และมีมุมที่เท่ากันดังรูป

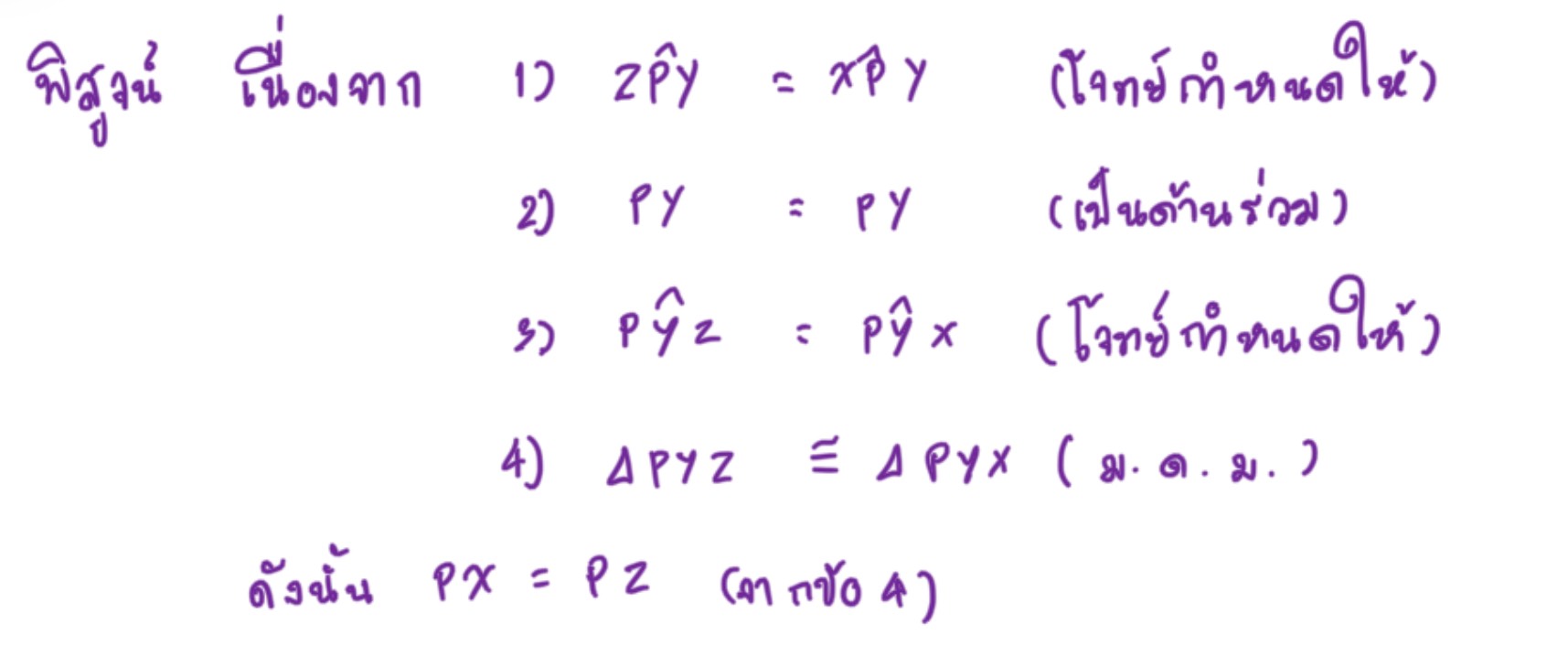
ตัวอย่างที่ 2

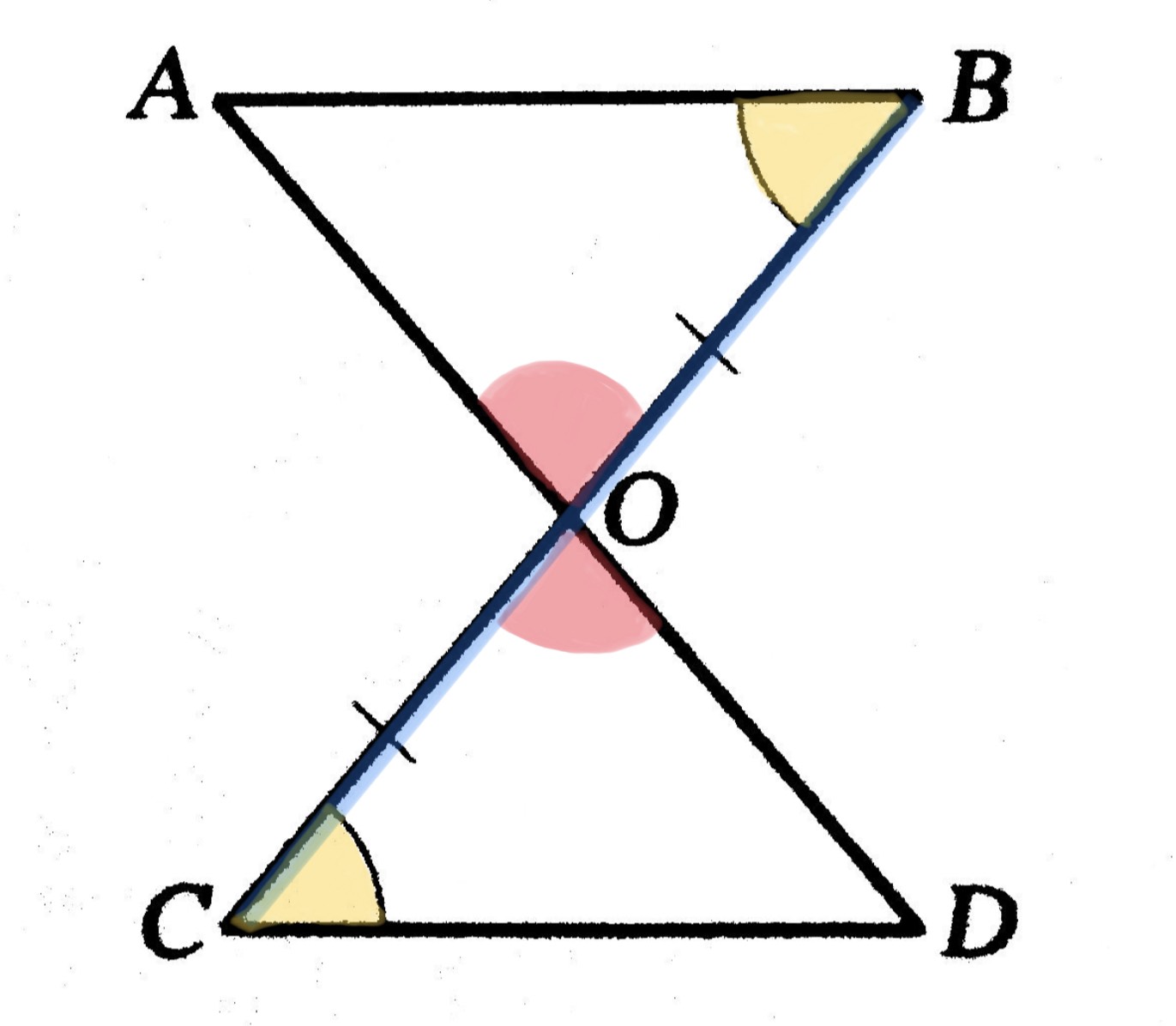
กำหนดให้ มุมABO = มุมOCD และด้าน BO = OC ตามรูป จงพิสูจน์ว่า AB = CD

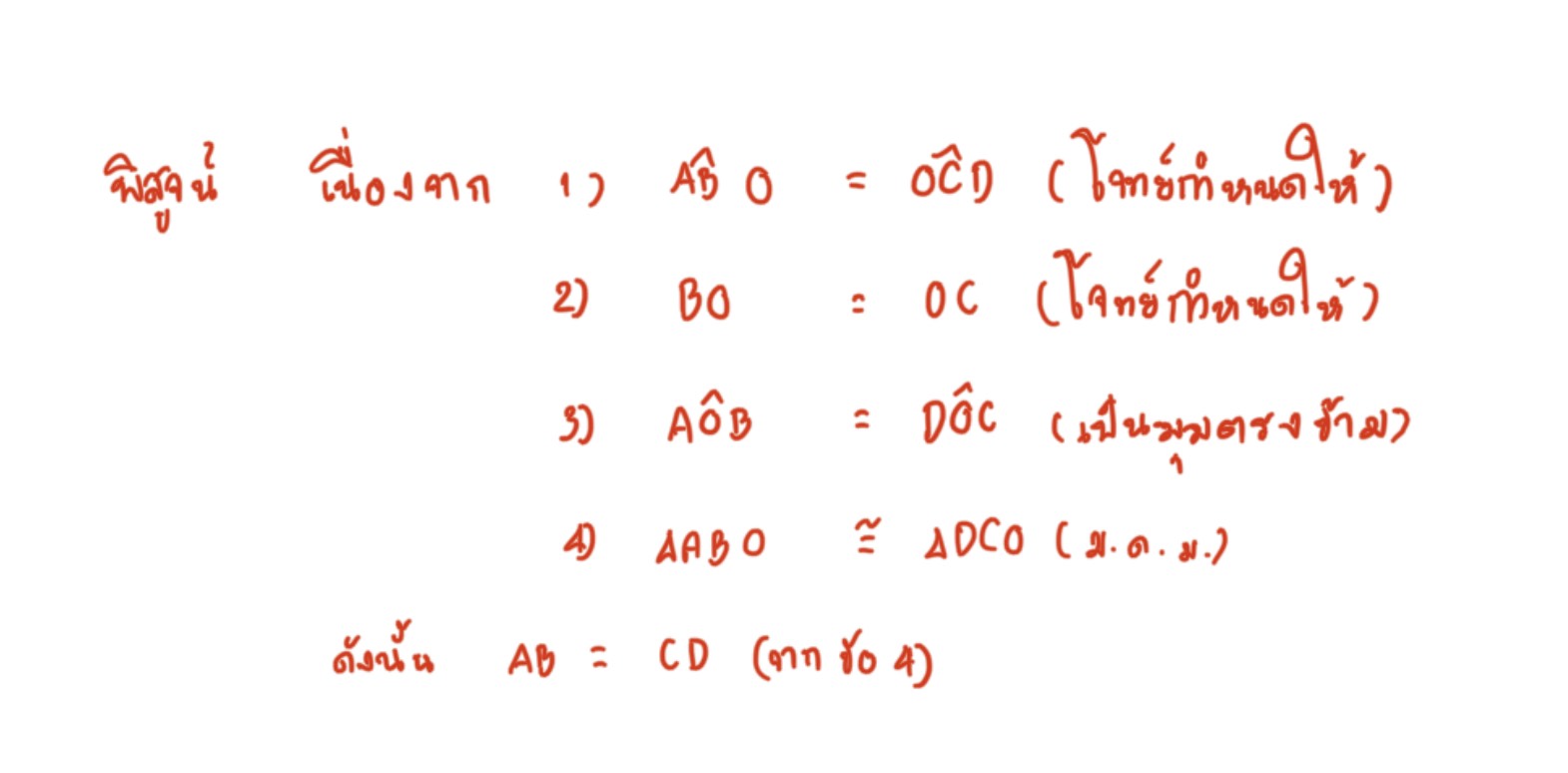
ตัวอย่างที่ 3

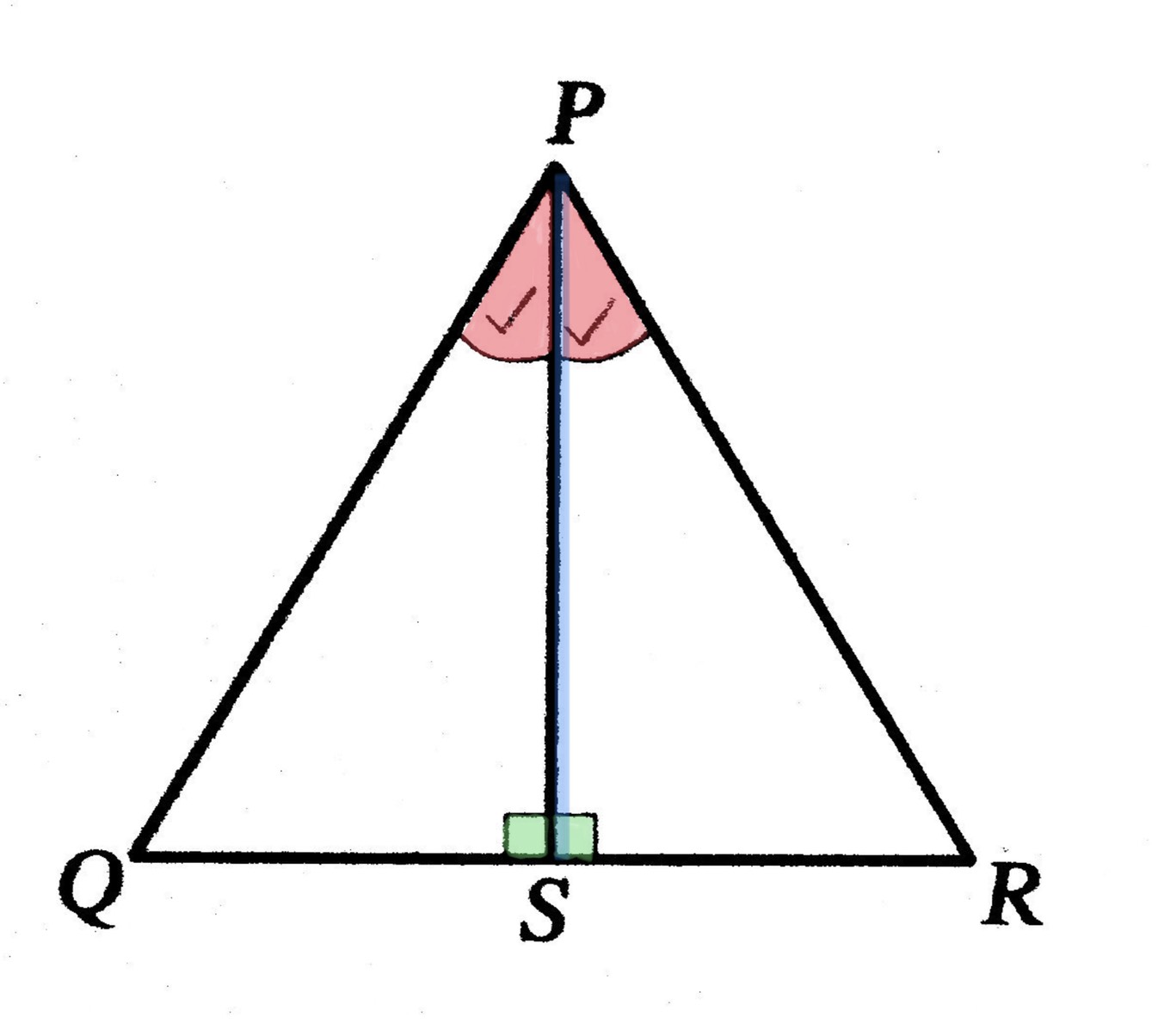
กำหนดให้ มุมQPS = มุมSPR และ มุมPSQ = มุมPSR = 90องศา อยากทราบว่า สามเหลี่ยมPQR เป็นรูปสามเหลี่ยมหน้าจั่วหรือไม่

ตัวอย่างที่ 4

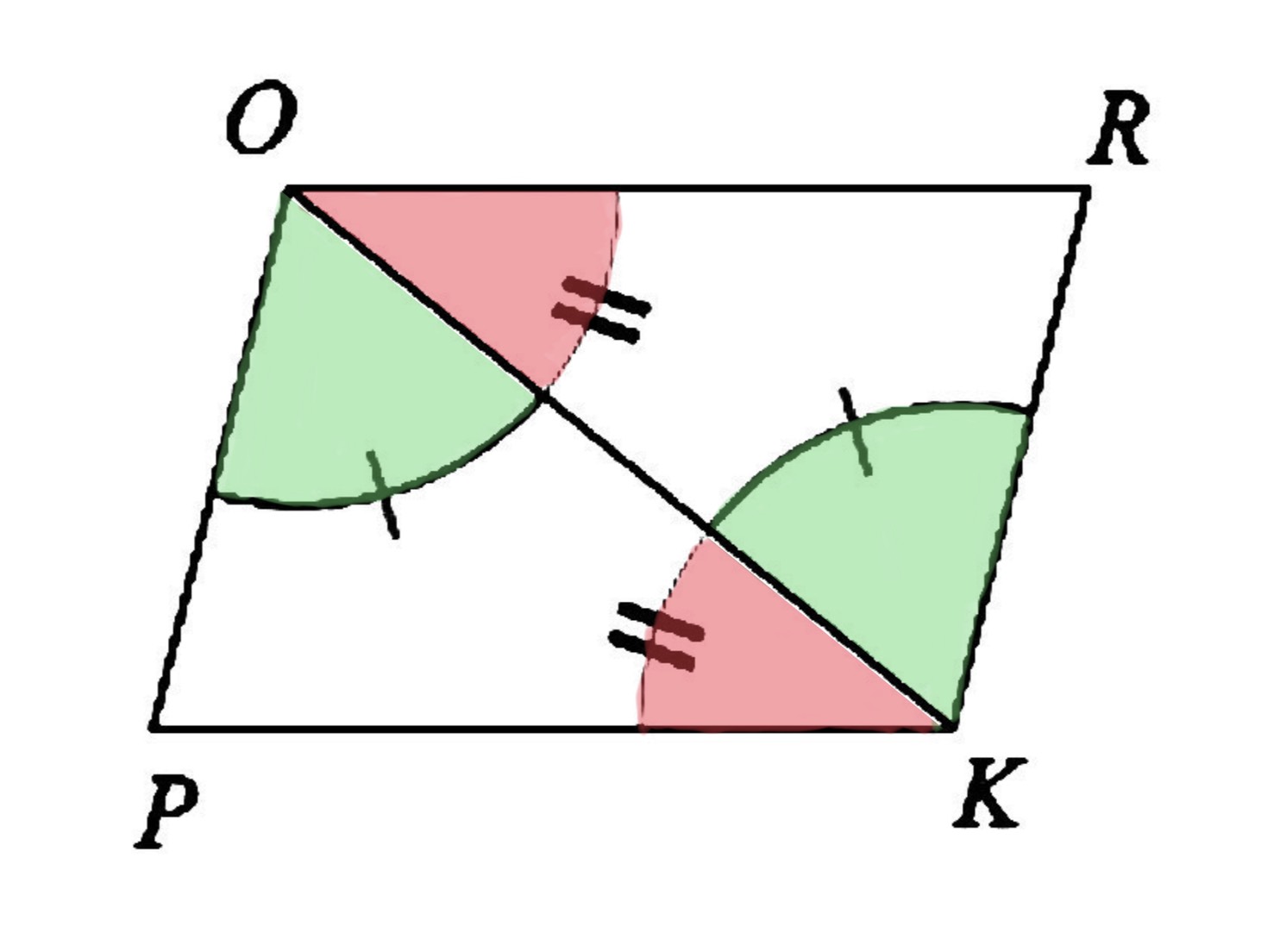
จากรูปกำหนดให้ มุมPOK = มุมRKO และ มุมOKP = มุมKOR จงพิสูจน์ว่าสามเหลี่ยมOPK และสามเหลี่ยมKROเป็นสามเหลี่ยมที่เท่ากันทุกประการ

คลิปวิดีโอตัวอย่างเรื่องสามเหลี่ยมที่เท่ากันทุกประการแบบ มุม-ด้าน-มุม

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

โคลงนฤทุมนาการ โคลงสุภาษิตสอนใจรู้ไว้ไม่เป็นทุกข์

หลังจากได้ศึกษาเรื่องโคลงโสฬสไตรยางค์ไปแล้ว น้อง ๆ ทราบไหมคะว่าในโครงสุภาษิตยังมีเรื่องอื่นอีกด้วย และในบทเรียนที่น้อง ๆ จะได้เรียนต่อไปนี้ก็คือเรื่อง โคลงนฤทุมนาการ เป็นโคลงสุภาษิต ที่ใช้โคลงสี่สุภาพในการประพันธ์เหมือนโคลงโสฬสไตรยางค์ แต่จะมีความหมาย และเนื้อหาอย่างไรบ้าง ไปเรียนรู้พร้อม ๆ กันเลยค่ะ โคลงนฤทุมนาการ คืออะไร ก่อนที่จะไปเรียนรู้ว่าในโคลงนฤทุมนาการมีอะไรบ้างนั้น เรามาดูกันที่ความหมายก่อนเลยค่ะ คำว่า นฤทุมนาการ มาจากคำศัพท์ต่าง

ราชาศัพท์ คำใดบ้างที่เราควรรู้?

น้อง ๆ หลายคนคงจะเคยได้ยินคำราชาศัพท์มาบ้างเวลาที่เปิดโทรทัศน์ดูข่าวช่วงหัวค่ำ แต่เคยสงสัยกันบ้างไหมคะว่า ราชาศัพท์ ที่นักข่าวในโทรทัศน์พูดกันบ่อย ๆ มีความหมายว่าอะไรบ้าง บทเรียนภาษาไทยในวันนี้จะพาน้อง ๆ ไปเรียนรู้เกี่ยวกับคำราชาศัพท์ เพื่อที่เวลาน้อง ๆ ฟังข่าว จะได้เข้าใจได้ง่ายมากขึ้น เราไปเรียนรู้พร้อมกันเลยค่ะ ราชาศัพท์ การแบ่งลำดับขั้นของบุคคลในการใช้คำราชาศัพท์ แบ่งออกได้เป็น 5 ระดับ ดังนี้

ตัวบ่งปริมาณและค่าความจริงของตัวบ่งปริมาณ

ตัวบ่งปริมาณ ตัวบ่งปริมาณ คือ สัญลักษณ์หรือข้อความที่เมื่อเราเอาไปเติมใน “ประโยคเปิด” แล้วจะทำให้ประโยคนั้นกลายเป็นประพจน์ ประโยคเปิด คือประโยคบอกเล่าหรือปฏิเสธที่ติดค่าตัวแปรที่ยัง “ไม่รู้ว่าเป็นจริงหรือเท็จ” โดยตัวแปรนั้นเป็นสมาชิกของเอกภพสัมพัทธ์ (Universe : U) ประโยคเปิด ยังไม่ใช่ประพจน์ (แต่เกือบเป็นแล้ว) เพราะเรายังไม่รู้ว่าเป็นจริงหรือเท็จ เช่น “x มากกว่า 3” จะเห็นว่าตัวแปร คือ x ซึ่งเราไม่รู้ว่า x

เปรียบเทียบเศษส่วนและจำนวนคละฉบับเข้าใจง่ายและเห็นภาพ

บทความนี้จะพาน้องๆ มาทำความเข้าใจเกี่ยวกับเรื่องการเปรียบเทียบเศษส่วนและจำนวนคละ เนื่องจากหลักการที่ใช้ในการเปรียบเทียบเศษส่วนนี้จะนำไปต่อยอดกับเรื่องต่อไปเช่นเรื่องการบวกและการลบเศษส่วน หลังจากอ่านบทความนี้จบสิ่งที่จะได้รับก็คือ หลักการเปรียบเทียบเศษส่วน วิธีเปรียบเทียบที่เห็นภาพและเข้าใจง่ายร่วมถึงเทคนิคที่จะช่วยให้น้อง ๆ สามารถเปรียบเทียบเศษส่วนได้เร็วยิ่งขึ้น