เมื่อเราได้ทำความเข้าใจและเรียนรู้เนื้อหาของหลักการหารทศนิยมแล้วเรื่องต่อไปก็จะเป็นการวิเคราะห์โจทย์ปัญหาการหารทศนิยม เพราะจะได้นำเอาหลักการหารทศนิยมมาให้ในการแก้โจทย์ปัญหา ซึ่งโดยส่วนใหญ่โจทย์ปัญหาที่นำมาก็จะเป็นการยกตัวอย่างเหตุการณ์ในชีวิตจริง เช่นการหาค่าเฉลี่ย การแบ่งเงิน และการชั่ง ตวงและการวัด เป็นต้น
ตัวอย่างโจทย์ปัญหาการหารทศนิยม
ตัวอย่างที่ 1
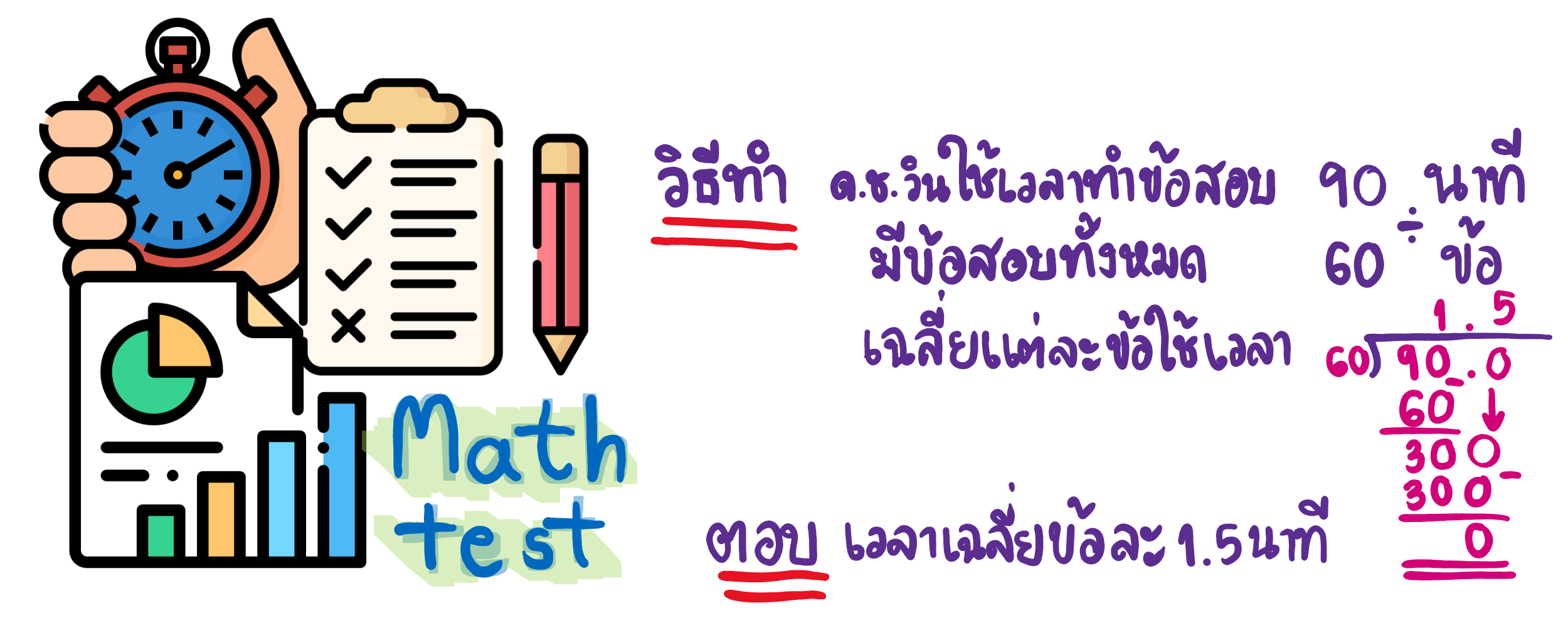
ข้อสอบคณิตศาสตร์ 60 ข้อ กำหนดเวลาทำข้อสอบ 100 นาที ด.ช.วิน ทำเสร็จภายในเวลา 90 นาที ด.ช.วิน ทำข้อสอบเฉลี่ยข้อละกี่นาที
วิเคราะห์โจทย์: โจทย์ต้องการทราบค่าเฉลี่ยของเวลาในการทำข้อสอบ ดังนั้นต้องนำ 90 ไปแบ่งให้ 60 ข้อ เท่าๆกัน คือหลักการหารทศนิยม
ประโยคสัญลักษณ์: 90 ÷ 60 = _______________
ตัวอย่างที่ 2
พี่หญิงมีน้ำผลไม้อยู่ 3 ลิตร แบ่งให้น้อง 7 คน เท่าๆกัน น้องแต่ละคนจะได้รับน้ำผลไม้คนละกี่มิลลิลิตร (ตอบเป็นทศนิยม 2 ตำแหน่ง)
วิเคราะห์โจทย์: โจทย์กำหนดว่าให้แบ่งน้ำผลไม้ให้เท่าๆกัน ตรงกับหลักการหาร และหน่วยที่ต้องการทราบคือหน่วยมิลลิลิตร ดังนั้นต้องแปลงหน่วยที่โจทย์ให้มา จากลิตรเป็นมิลลิลิตรก่อนจึงจะนำไปแบ่งให้ท่าๆกันได้
ประโยคสัญลักษณ์: (3 x 1,000) ÷ 7 = _______________

ตัวอย่างที่ 3
วันที่ 21 กันยายน 2563 เงิน 1 ดอลล่าร์สหรัฐ(USD) แลกเป็นเงินไทยได้ประมาณ 31 บาท วินัยนำเงิน 32,500 บาท แลกเป็นเงิน ดอลล่าร์สหรัฐได้ประมาณกี่ดอลลาร์ (ตอบเป็นทศนิยม 2 ตำแหน่ง)
วิเคราะห์โจทย์: ต้องนำเงินไทยแลกทีละ 31.09 บาท ถึงจะได้เป็นเงิน 1 ดอลลาร์ ดังนั้นต้องแบ่งออกทีละเท่าๆกัน คือหลักการหาร
ประโยคสัญลักษณ์: 32,500 ÷ 31 = _______________

ตัวอย่างที่ 4
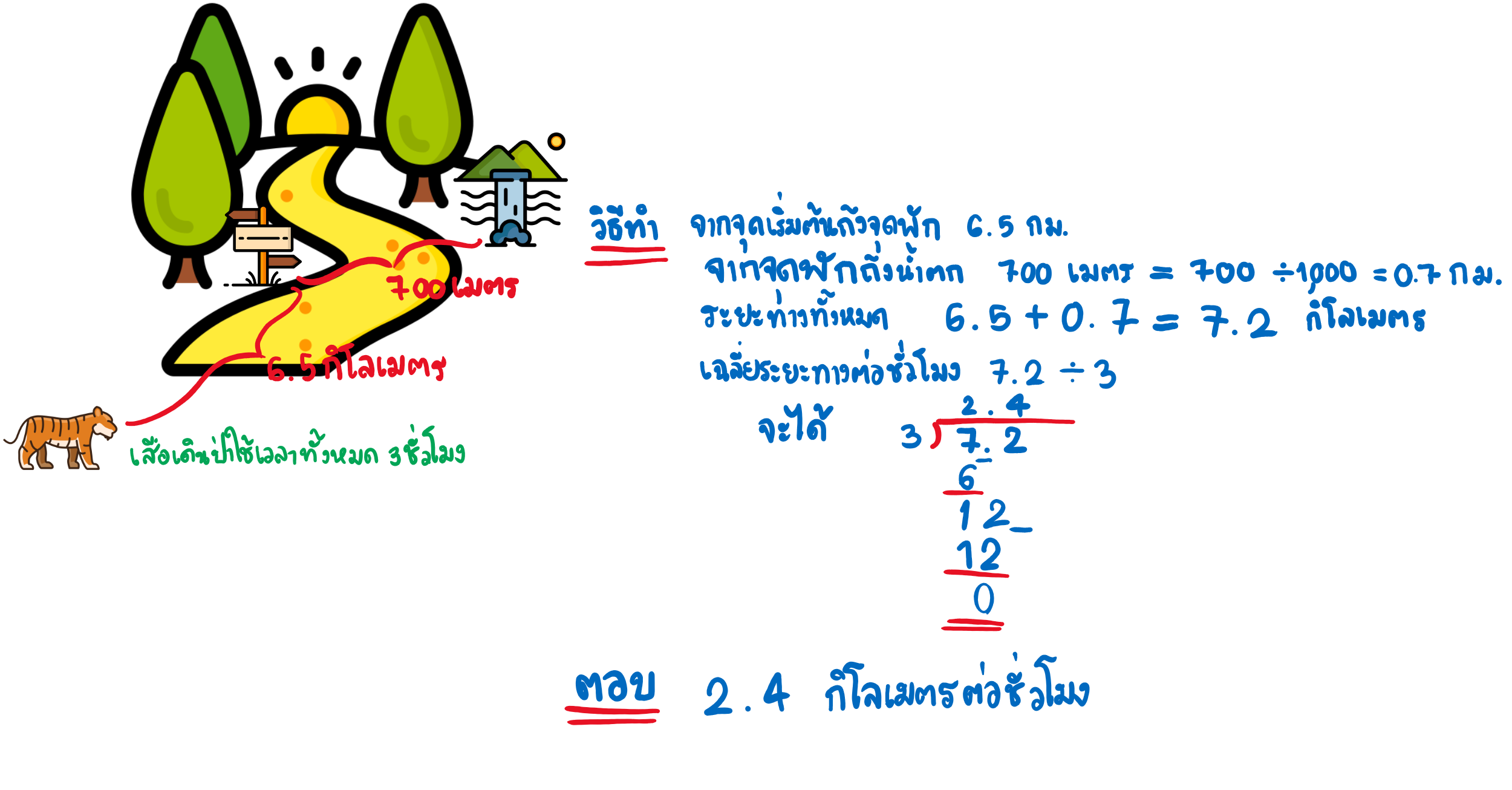
เสือเดินป่าจากจุดเริ่มต้นถึงจุดพักเป็นระยะทาง 6.5 กิโลเมตร จากนั้นดินต่ออีก 700 เมตร จนถึงน้ำตก ใช้เวลาเดินป่าจากจุดเริ่มต้นถึงน้ำตก 3 ชั่วโมง เสือใช้เวลาเดินป่าเฉลี่ยชั่วโมงละกี่กิโลเมตร
วิเคราะห์โจทย์: โจทย์ต้องการทราบค่าเฉลี่ยของเวลาในการเดินป่าของเสือ ดังนั้นต้องนำระยะทางทั้งหมด (แต่ต้องทำหน่วยให้เหมือนกันก่อนจึงจะสามารถนำไปแบ่งได้) ไปแบ่งให้วลา 3 ชั่วโมง เท่าๆกัน คือหลักการหาร
ประโยคสัญลักษณ์: [6.5 + ( 700 ÷ 1,000 )] ÷ 3 = _______________