การนำเสนอข้อมูลเเละเเปลความหมายข้อมูลด้วยเเผนภูมิวงกลม
การนำเสนอข้อมูลเเละเเปลความหมายข้อมูลด้วยเเผนภูมิวงกลม เป็นการนำเสนอข้อมูลโดยการเเบ่งพื้นที่ของวงกลมออกเป็นส่วน ๆ เเละมีขนาดของสัดส่วนตามข้อมูลที่ได้ทำการเก็บรวบรวมข้อมูลไว้ การนำเสนอด้วยเเผนภูมิวงกลมเป็นการนำเสนอข้อมูลที่มีอยู่ได้อย่างน่าสนใจ สามารถวิเคราะห์เเละเเปรข้อมูลได้ง่ายขึ้น
การสร้างแผนภูมิรูปวงกลมเพื่อนำเสนอข้อมูล
การสร้างแผนภูมิวงกลม ทำได้โดยการเเบ่งมุมรอบจุดศูนย์กลางของวงกลมที่มีขนาด 360 องศา ออกเป็นส่วน ๆ ที่เรียกว่า มุมที่จุดศูนย์กลางของวงกลม ตามขนาดที่ได้จากการเทียบส่วนกับปริมาณทั้งหมดในข้อมูล
มุมที่จุดศูนย์กลาง = (จำนวนที่สนใจ/จำนวนทั้งหมด) x 360 องศา
ตัวอย่างการสร้างแผนภูมิวงกลม
จากข้อมูลการสำรวจที่ได้เก็บรวมรวบข้อมูลจากนักเรียนทั้งหมด 200 คน เกี่ยวกับเครื่องดื่มที่นักเรียนชื่นชอบ โดยนักเรียนเเต่ละคนสามารถเลือกได้เพียง 1 ตัวเลือก พบว่านักเรียนเเต่ละคนชอบเครื่องดื่มดังนี้
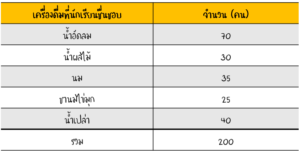
วิธีทำ เริ่มจากการหามุมที่จุดศูนย์กลางของวงกลม สำหรับข้อมูลเเต่ละชุดก่อน โดยมุมภายในทั้งหมดรวมกันต้องได้ 360 องศา
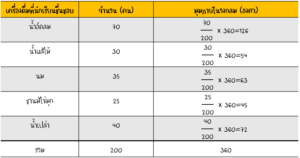
หลังจากนั้นให้เราสร้างวงกลมขึ้น เเละลากเส้นรัศมีของวงกลมให้ทำมุมกันตาม มุมภายในวงกลม ที่ได้จากการคำนวณ
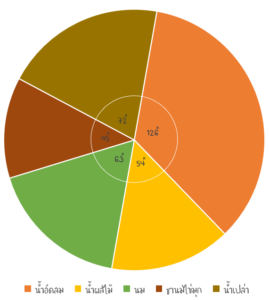
สุดท้ายให้เรานำข้อมูลที่อยู่ในตารางลงไปใส่ในวงกลม อาจจะเป็น จำนวนคนหรือเเปลงเป็นเปอร์เซ็นต์ เพื่อความสวยงามเเละง่ายต่อการอ่านข้อมูล
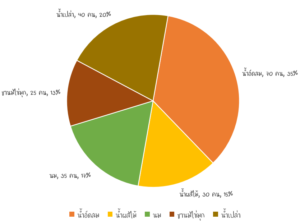
ตัวอย่างการนำเสนอข้อมูลเเละเเปลความหมายข้อมูลด้วยเเผนภูมิวงกลม
ตัวอย่าง จากการสำรวจข้อมูลประชากรสัญชาติไทยที่เล่นเกม ROW ในปีพ.ศ. 2565 มีผู้เล่นเกมเป็นดังนี้
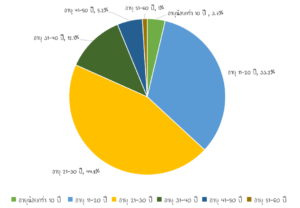
คำถามที่ 1 ประชากรส่วนใหญ่ของประเทศไทยที่เล่นเกม ROW มีอายุเท่าใดเเละประชากรกลุ่มใดเล่นเกม ROW น้อยที่สุด
ตอบ ประชากรส่วนใหญ่ของประเทศไทยที่เล่นเกม ROW มีอายุ 21-30 ปี เเละประชากรที่เล่นเกม ROW น้อยที่สุดมีอายุ 51 – 60 ปี
คำถามที่ 2 ถ้าช่วงประชากรไทยช่วงอายุ 11-20 ปีที่เล่น ROW มีจำนวน 3.32 ล้านคน จะมีประชากรไทยช่วงอายุ 31-40 ปีที่เล่น ROW จำนวนกี่คน
วิธีทำ จากแผนภูมิวงกลมอัตราส่วนระหว่างประชากรไทยช่วงอายุ 11-20 ปีที่เล่น ROW ต่อประชากรไทยช่วงอายุ 31-40 ปีที่เล่น ROW จะมีค่า
= 33.2 : 12.1
ถ้าประชากรไทยช่วงอายุ 11-20 ปีที่เล่น ROW มีจำนวน 3.32 ล้านคน
อัตราส่วนใหม่จะมีค่า
= 3,320,000 : a (ให้จำนวนประชากรไทยช่วงอายุ 31-40 ปีมีค่าเป็น a)
ดังนั้นประชากรไทยช่วงอายุ 31-40 ปีที่เล่น ROW จะมีจำนวน
= (3,320,000/33.2) x 12.1
= 1,210,000 คน
ตอบ ประชากรไทยช่วงอายุ 31-40 ปีที่เล่น ROW มีจำนวน 1,210,000 คน
คำถามที่ 3 ถ้าจำนวนประชากรในปีที่ทำการสำรวจนี้เท่ากับ 12 ล้านคน เเล้วจำนวนประชากรในช่วงอายุ 21-30 ปี ที่เล่นเกม ROW มีทั้งหมดกี่คน
วิธีทำ จากแผนภูมิวงกลมจำนวนประชากรในช่วงอายุ 21-30 ปีมีจำนวน 44.8%
ดังนั้นจำนวนประชากรในช่วงอายุ 21-30 ปีมีจำนวน = (44.8 x 12 ล้านคน)/100
= 5,376,000 คน
ตอบ จำนวนประชากรในช่วงอายุ 21-30 ปี ที่เล่นเกม ROW มีทั้งหมด 5,376,000 คน
การนำเสนอด้วยเเผนภูมิรูปวงกลม เหมาะสำหรับการเปรียบเทียบข้อมูลเชิงคุณภาพเเต่ละกลุ่มกับภาพรวมของข้อมูลทั้งหมด ซึ่งหากข้อมูลมีจำนวนเยอะมาก ๆ การนำเสนอด้วยแผนภูมิรูปวงกลมอาจไม่เหมาะ เพราะว่าเราต้องเเบ่งวงกลมออกเป็นหลาย ๆ ส่วนทำให้เปรียบเทียบความต่างของข้อมูลได้ยาก
บทความนี้ได้รวบรวมเนื้อหาของ การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิวงกลม จะเห็นได้ว่ามีส่วนสำคัญในการเเก้ปัญหาที่จะเกิดขึ้นในอนาคตได้ หากวิเคราะห์ข้อมูลได้อย่างมีประสิทธิภาพ ในส่วนของการสร้างแผนภูมิวงกลมเเละตัวอย่างการเเปรความหมายน้อง ๆ สามารถศึกษาเพิ่มเติมได้จากวิดีโอนี้
คลิปวิดีโอ การนำเสนอข้อมูลเเละเเปรความหมายข้อมูลด้วยเเผนภูมิวงกลม
คลิปวิดีโอนี้ได้รวบรวมวิธี การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิวงกลม ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยความรู้ เเละเทคนิครวมถึงการอธิบาย ตัวอย่าง เเละสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย