การแจกแจงความถี่ของข้อมูล (Frequency distribution)
การแจกแจงความถี่ของข้อมูล เป็นวิธีการทางสถิติอย่างหนึ่งที่ใช้ในการจัดข้อมูลที่มีอยู่ให้เป็นหมวดหมู่ เพื่อความสะดวกในการนำเสนอและการวิเคราะห์ข้อมูลเหล่านั้น มี 2 ลักษณะ คือ ตารางแจกแจงความถี่แบบไม่เป็นอันตรภาคชั้น และ ตารางแจกแจงความถี่แบบไม่เป็นอันตรภาคชั้น
การสร้างตารางแจกแจงความถี่ แบบไม่เป็นอันตรภาคชั้น
การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ แบบไม่เป็นอันตรภาคชั้น เหมาะสำหรับข้อมูลที่มีค่าจาการสังเกตไม่มากนักหรือไม่ซับซ้อน
1. สุนิสาสำรวจอายุเป็นปีของคนที่มาออกกำลังกายเดิน วิ่งและเต้นแอโรบิกในสวนสาธารณะแห่งหนึ่งจำนวน 40 คน เป็นดังนี้
| 16 | 25 | 30 | 45 | 20 | 59 | 48 | 18 | 48 | 30 |
| 50 | 45 | 16 | 50 | 40 | 65 | 68 | 50 | 30 | 48 |
| 16 | 18 | 60 | 50 | 45 | 30 | 20 | 30 | 20 | 19 |
| 48 | 50 | 20 | 61 | 19 | 50 | 45 | 48 | 50 | 38 |
ให้สร้างตารางแจกแจงความถี่ พร้อมทั้งตอบคำถาม
|
อายุ (ปี) |
รอยขีด | ความถี่ |
|
16 |
lll |
3 |
|
18 |
ll |
2 |
|
19 |
ll |
2 |
|
20 |
llll |
4 |
|
25 |
l |
1 |
|
30 |
lllll |
5 |
|
38 |
l |
1 |
|
40 |
l |
1 |
|
45 |
llll |
4 |
|
48 |
lllll |
5 |
|
50 |
lllll ll |
7 |
|
59 |
l |
1 |
|
60 |
l |
1 |
|
61 |
l |
1 |
|
65 |
l |
1 |
|
68 |
l |
1 |
| รวม |
40 |
- ผู้ที่มาออกกำลังกายที่มีอายุน้อยที่สุดคืออายุเท่าไร (ตอบ 16 ปี)
- ผู้ที่มาออกกำลังกายที่มีอายุมากที่สุดคืออายุเท่าไร (ตอบ 68 ปี)
- ผู้ที่มาออกกำลังส่วนใหญ่มีอายุเท่าไร (ตอบ 50 ปี)
น้องๆจะพบเห็น การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ แบบไม่เป็นอันตรภาคชั้น ในชีวิติประจำวันได้บ่อยครั้ง เช่น การนับคะแนนเสียงเลือกตั้งประธานนักเรียน
การสร้างตารางแจกแจงความถี่ แบบเป็นอันตรภาคชั้น
การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ แบบเป็นอันตรภาคชั้น เหมาะสำหรับข้อมูลที่มีเป็นจำนวนมาก การสร้างตารางแจกแจงความถี่แบบเป็นอันตรภาคชั้นจะทำให้เสียเวลามาก จึงแจกแจงโดยการแบ่งค่าที่เป็นไปได้ทั้งหมดออกเป็นช่วงๆ แต่ละช่วงเรียกว่า “ อันตรภาคชั้น ”
การสร้างตารางแจกแจงความถี่ มีวิธีการดังนี้
ขั้นที่ 1 หาข้อมูลสูงสุดและต่ำสุด
ขั้นที่ 2 หาพิสัยซึ่ง พิสัย = ข้อมูลสูงสุด – ข้อมูลต่ำสุด
ขั้นที่ 3 กำหนดจำนวนชั้น โดยปกติจำนวนชั้นจะอยู่ระหว่าง 5 – 15 ชั้น ซึ่งแบ่งเป็น
– ถ้ากำหนดจำนวนชั้นให้จะต้องหาความกว้างของอันตรภาคชั้น ดังนี้
ความกว้างของอันตรภาคชั้น = 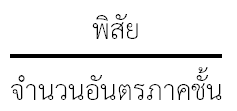
ถ้ากำหนดความกว้างของอันตรภาคชั้นให้ จะต้องหาจำนวนชั้น ดังนี้
จำนวนอันตรภาคชั้น = 
ผลลัพธ์ที่ได้จากการหารทั้ง 2 วิธี ถ้าเป็นทศนิยมจะต้องปัดให้เป็นจำนวนเต็มเสมอ
ขั้นที่ 4 เขียนอันตรภาคชั้นจากชั้นข้อมูลต่ำสุดไปหาชั้นข้อมูลสูงสุด หรือจากชั้นของข้อมูลสูงสุดไปหาชั้นข้อมูลต่ำสุดก็ได้
ขั้นที่ 5 พิจารณาข้อมูลแต่ละจำนวน ว่าจำนวนใดอยู่ในช่วงข้อมูลใดแล้วขีดลงในช่องรอยขีดของข้อมูล โดยให้หนึ่งขีดแทนข้อมูล 1 จำนวน
ขั้นที่ 6 จำนวนรอยขีดแต่ละชั้น คือ ความถี่ของข้อมูลในชั้นนั้น
2. ผลการสอบวิชาภาษาไทยของนักเรียนชั้นมัธยมศึกษาปีที่ 3 ของโรงเรียนแห่งหนึ่งเป็นดังนี้
68 84 75 82 68 91 61 89 75 93
73 79 87 77 60 92 70 58 82 75
61 65 74 86 72 62 90 78 63 72
96 78 89 61 75 95 60 79 85 71
65 80 73 57 88 63 62 76 54 74
การสร้างตารางแจกแจงความถี่ของข้อมูลดังกล่าวควรใช้อันตรภาคชั้นที่เป็นช่วงคะแนน ซึ่งมีลำดับขั้นตอนดังต่อไปนี้
- หาค่าสูงสุด คือ 96 และค่าต่ำสุด คือ 54
- พิสัย = ค่าสูงสุด – ค่าต่ำสุด
= 96 – 54
= 42
- กำหนดความกว้างของอันตรภาคชั้น = 10
จำนวนอันตรภาคชั้น = = 4.2
จะได้จำนวนอันตรภาคชั้นเป็น 5 ชั้น
- เรียงลำดับอันตรภาคชั้นจากคะแนนน้อยไปมาก
- นำข้อมูลดิบมาใส่ตาราง โดยขีดรอยขีดของคะแนนในอันตรภาคชั้นที่มีความกว้าง ครอบคลุม ข้อมูลนั้นอยู่
- รวบรวมความถี่ของรอยคะแนน เพื่อนำไปแปลความหมายของข้อมูลต่อไป
|
คะแนน |
รอยขีด |
ความถี่ |
|
51 – 60 61 – 70 71 – 80 81 – 90 91 – 100 |
///// ///// ///// // ///// ///// ///// /// ///// ///// ///// |
5 12 18 10 5 |
3. จากผลการสอบวิชาคณิตศาสตร์พื้นฐานของนักเรียน ม. 3/9 จำนวน 40 คน เป็นดังนี้
35 100 56 49 64 85 64 65 51 84
95 84 66 72 83 89 64 66 73 87
65 87 56 78 77 69 69 56 47 95
47 79 76 55 83 68 75 76 41 72
จงสร้างตารางแจกแจงความถี่ให้มีจำนวนชั้นเป็น 7
วิธีทำ คะแนนสูงสุดเท่ากับ 100 และ คะแนนต่ำสุดเท่ากับ 35
ดังนั้น พิสัย = 100 – 35 = 65
ความกว้างของอันตรภาคชั้น เท่ากับ 9.3
จะได้ความกว้างของอันตรภาคชั้นเป็น 10
|
คะแนน |
รอยขีด |
ความถี่ |
|
35 – 44 |
// | 2 |
|
45 – 54 |
//// | 4 |
|
55 – 64 |
///// // | 7 |
|
65 – 74 |
///// ///// |
10 |
| 75 – 84 |
///// ///// |
10 |
|
85 – 94 |
//// |
4 |
| 95 – 104 |
/// |
3 |
|
N = 40 |
4. ข้อมูลต่อไปนี้เป็นคะแนนสอบวิชาคณิตศาสตร์ ซึ่งมีคะแนนเต็ม 100 คะแนนของนักเรียนจำนวน 40 คนดังนี้
84 79 65 78 78 62 80 67 82 73 81 68 60 74 67 75 48 80 71 62
76 76 65 63 68 51 48 53 71 75 74 77 68 73 61 66 75 79 52 62
จงสร้างตารางแจกแจงความถี่ให้มี 8 อันตรภาคชั้น
วิธีทำ คะแนนสูงสุดเท่ากับ 84 และ คะแนนต่ำสุดเท่ากับ 48
ดังนั้น พิสัย = 84 – 48 = 36
ความกว้างของอันตรภาคชั้น เท่ากับ = 4.5
จะได้ความกว้างของอันตรภาคชั้นเป็น 5
| อันตรภาคชั้น | รอยขีด |
ความถี่ |
|
45 – 49 |
ll |
2 |
|
50 – 54 |
lll |
3 |
| 55 – 59 |
0 |
|
|
60 – 64 |
lllll l |
6 |
| 65 – 69 |
lllll lll |
8 |
|
70 – 74 |
lllll l |
6 |
|
75 – 79 |
lllll lllll |
10 |
| 80 – 84 |
lllll |
5 |
|
N = 40 |
||
จงตอบคำถามต่อไปนี้
- นักเรียนส่วนใหญ่มีคะแนนสอบอยู่ในช่วงใด (ตอบ 75 – 79 คะแนน)
- นักเรียนที่ได้คะแนนต่ำกว่า 65 คะแนน มีกี่คน (ตอบ 11 คน)
- นักเรียนที่ได้คะแนนสูงกว่า 69 คะแนน มีกี่คน (ตอบ 21 คน)
ตารางแจกแจงความถี่ เป็นตาราง การนำเสนอข้อมูลทางสถิติ หรือข้อมูลดิบ เพื่อให้เกิดความสะดวกในการนำไปใช้ เมื่อข้อมูลดิบเป็นตัวเลขที่แสดงปริมาณ และมีจำนวนข้อมูลมาก ๆ และไม่ค่อยซ้ำกัน การสร้างตารางแจกแจงความถี่ควรใช้อันตรภาคชั้นที่เป็นส่วนของช่วงคะแนน
การหาขอบล่าง ขอบบน และจุดกึ่งกลาง
เราสามารถหาขอบล่าง – ขอบบน ได้จากสูตร
ขอบล่าง = 
ขอบบน = 
จุดกึ่งกลางชั้น = 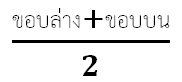
5. ให้นักเรียนพิจารณาตารางแจกแจงความถี่ของความสูงของนักเรียนมัธยมตอนต้น ของโรงเรียน
แห่งหนึ่ง จำนวน 100 คน ดังต่อไปนี้
|
ความสูง (ซม.) |
จำนวนนักเรียน (คน) |
|
140 – 144 145 – 149 150 – 154 155 – 159 160 – 164 |
5 18 42 27 8 |
ขอบล่างของอันตรภาคชั้น 150 – 154 คือ = 149.5
ขอบบนของอันตรภาคชั้น 150 – 154 คือ = 154.5
อาจเขียนข้อมูลในตารางแจกแจงความถี่ข้างต้นให้เห็นขอบล่างและขอบบนของข้อมูลได้ ดังนี้
|
ความสูง (ซม.) |
จำนวนนักเรียน (คน) |
|
139.5 – 144.5 144.5 – 149.5 149.5 – 154.5 154.5 – 159.5 159.5 – 164.5 |
5 18 42 27 8 |
จากข้อมูลข้างต้นเขียนตารางแสดงขอบล่าง – ขอบบน จุดกึ่งกลางชั้น และความถี่ ได้ดังนี้
|
ขอบล่าง-ขอบบน |
จุดกึ่งกลางชั้น | จำนวนนักเรียน (คน) |
| 139.5 – 144.5
144.5 – 149.5 149.5 – 154.5 154.5 – 159.5 159.5 – 164.5 |
142
147 152 157 162 |
5 18 42 27 8 |
6. จากตารางแจกแจงความถี่ต่อไปนี้จงหาขอบล่าง ขอบบน และจุดกึ่งกลาง
| อายุ | ความถี่ |
| 10 – 19 | 12 |
| 20 – 29 | 15 |
| 30 – 39 | 18 |
| 40 – 49 | 24 |
| 50 – 59 | 10 |
| 60 – 69 | 11 |
| รวม | 90 |
วิธีทำ
|
อายุ |
ความถี่ | ขอบล่าง-ขอบบน | จุดกึ่งกลางชั้น |
| 10 – 19 | 12 | 9.5 – 19.5 |
14.5 |
|
20 – 29 |
15 | 19.5 – 29.5 | 24.5 |
| 30 – 39 | 18 | 29.5 – 39.5 |
34.5 |
|
40 – 49 |
24 | 39.5 – 49.5 | 44.5 |
| 50 – 59 | 10 | 49.5 – 59.5 |
54.5 |
|
60 – 69 |
11 | 59.5 – 69.5 | 64.5 |
| รวม | 90 |
|
|
7. จากตารางแจกแจงความถี่ที่กำหนดให้ จงหาขอบล่าง ขอบบน และจุดกึ่งกลางชั้น
|
คะแนน |
ความถี่ |
|
70 – 74 |
15 |
| 75 – 79 |
5 |
|
80 – 84 |
10 |
| 85 – 89 |
8 |
| 90 – 94 |
2 |
วิธีทำ
|
คะแนน |
ความถี่ | ขอบล่าง | ขอบบน | จุดกึ่งกลางชั้น |
| 70 – 74 | 15 | 69.5 | 74.5 |
72 |
|
75 – 79 |
5 | 74.5 | 79.5 | 77 |
| 80 – 84 | 10 | 79.5 | 84.5 |
82 |
|
85 – 89 |
8 | 84.5 | 89.5 | 87 |
| 90 – 94 | 2 | 89.5 | 94.5 |
92 |
การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ น้องๆได้เรียนรู้เรื่องการหารอยขีด ความถี่ ขอบบน ขอบล่าง และจุดกึ่งกลางชั้น ซึ่งน้องได้เรียนรู้การนำเสนอข้อมูลในรูปแบบอื่นมาแล้ว เช่น แผนภูมิแท่ง และ กราฟเส้น ซึ่งการนำเสนอข้อมูลในรูปแบบต่างๆมีการนำไปประยุกต์ใช้ในการทำงานที่แตกต่างกันออกไปตามความเหมาะสม